Элементы финансовой математики
Тема 9. Элементы финансовой математики (ВРЕМЕННАЯ ОЦЕНКА ДЕНЕЖНЫХ ПОТОКОВ)
Для понимания сущности методов оценки доходной недвижимости необходимо рассмотреть функции сложного процента, которые характеризуют количественные изменения стоимости денег во времени.
Базовая аксиома всей методологии оценки недвижимости – «деньги завтра не есть деньги сегодня». Приведение денежных сумм, возникающих в разное время, к сопоставимому виду называется временнòй оценкой денежных потоков. Временная оценка денежных потоков основана на использовании шести функций сложного процента или шести функций денежной единицы.
Для операций финансового анализа используются специальные таблицы шести функций, содержащие предварительно рассчитанные по сложному проценту факторы:
колонка 1 — накопленная сумма (будущая стоимость) денежной единицы (fvf, i, n);
колонка 2 — накопление денежной единицы (fvaf, i, n);
колонка 3 — фонд возмещения (sff, i, n);
колонка 4 — текущая стоимость единицы (реверсии) (pvf, i, n);
колонка 5 — текущая стоимость обычного аннуитета (pvaf, i, n);
колонка 6 — взнос на амортизацию единицы (iaof, i, n).
Рекомендуемые материалы
Таблицы, рассчитанные для годового и ежемесячного начисления процента, приведены в приложении.
Порядок использования таблиц:
1. Выбрать раздел ежегодного или ежемесячного учета накопления.
2. Найти страницу с соответствующей ставкой сложного процента.
3. Найти колонку, где указывается величина соответствующего фактора сложного процента.
4. Найти продолжительность расчетного срока в левой или число периодов в правой колонке выбранной таблицы.
5. Найти расчетную величину фактора сложного процента на пересечении соответствующей колонки и ряда таблицы.
6. Умножить величину единичного фактора на известную исходную денежную сумму, соответствующую данной ситуации в задаче.
1. Накопленная сумма денежной единицы
Базовые формулы:
а) при начислении процентов 1 раз в год:
FV = PV(1+i) n = PV (fvf, i, n),
б) при более частом, чем 1 раз в год, начислении процентов:
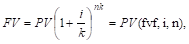 |
где n — число лет; к – количество начислений в году.
 (1+i) n — фактор накопленной суммы (будущей стоимости) денежной единицы при ежегодном начислении процентов;
(1+i) n — фактор накопленной суммы (будущей стоимости) денежной единицы при ежегодном начислении процентов;
— фактор накопленной суммы (будущей стоимости) денежной единицы при более частом, чем 1 раз в год, начислении процентов.
Данная функция используется в том случае, если известна текущая стоимость денег и требуется определить ее накопленную сумму (будущую стоимость) на конец определенного периода при заданной ставке дохода на капитал.
2. Текущая стоимость единицы (реверсии)
а) При начислении процентов 1 раз в год:
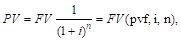 |
б) при более частом, чем 1 раз в год, начислении процентов:
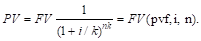 |
Смысл задач такого класса состоит в том, чтобы при заданной ставке дисконта дать оценку текущей стоимости тех денег, которые могут быть получены (заплачены) в конце определенного периода.
3. Текущая стоимость аннуитета
Аннуитет — серия равных платежей, вносимых или получаемых через равные промежутки времени в течение определенного периода. В том случае, если платежи (поступления) производятся в конце каждого периода, говорят об обычном аннуитете. Если же платежи (поступления) осуществляются авансом, т.е. в начале каждого периода, говорят об авансовом аннуитете.
Базовые формулы:
 а) при платежах (поступлениях) в конце каждого года:
а) при платежах (поступлениях) в конце каждого года:
где PMT - равновеликие периодические платежи (поступления);
б) при более частых, чем 1 раз в год, платежах (поступлениях):
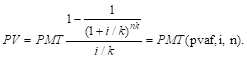 |
Расчет текущей стоимости авансового аннуитета.
а) при платежах (поступлениях) в начале каждого года:
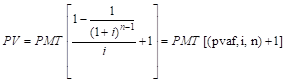 |
для (n-1)-го периода;
б) при более частых, чем 1 раз в год, платежах (поступлениях):
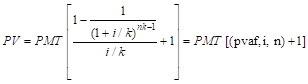 |
для (n-1)-го периода.
4. Накопление денежной единицы за период
На основе использования данной функции определяется будущая стоимость серии равновеликих периодических платежей (поступлении).
Расчет будущей стоимости обычного аннуитета.
Базовые формулы при платежах в конце периода:
а) при платежах (поступлениях), осуществляемых 1 раз в конце года:
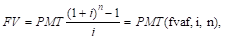 |
б) при платежах (поступлениях), осуществляемых чаще, чем 1 раз в год:
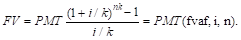 |
Расчет будущей стоимости авансового аннуитета.
Базовая формула:
а) при платежах (поступлениях), осуществляемых 1 раз в начале года:
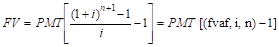 |
для (n + 1)-го периода;
б) при платежах (поступлениях), осуществляемых чаще, чем 1 раз в год:
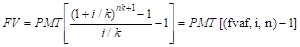 |
для (nk + 1)-го периода.
5. Взнос на амортизацию единицы
а) При платежах (поступлениях), осуществляемых 1 раз в год:
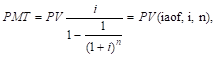 |
б) при платежах (поступлениях), осуществляемых чаще, чем 1 раз в год:
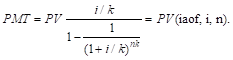 |
Данная функция используется для определения аннуитетных (регулярных равновеликих) платежей в счет погашения кредита, выданного на определенный период при заданной ставке по кредиту.
6. Формирование фонда возмещения
а) При платежах (поступлениях), осуществляемых 1 раз в год:
Вам также может быть полезна лекция "92 Участие прокурора в гражданском судопроизводстве".
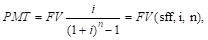 |
б) при платежах (поступлениях), осуществляемых чаще, чем 1 раз в год:
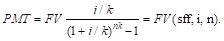 |
Данная функция используется для определения тех равномерных периодических платежей, которые необходимо осуществлять в течение заданного периода, чтобы к концу срока иметь на счете, приносящем доход по заданной ставке, определенную сумму денег.




















