Доверительное оценивание и доверительный интервал

6. Доверительное оценивание и доверительный интервал

Доверительное оценивание это метод математической статистики, предназначенный для построения множества при­ближённых значений неизвестных параметров вероятностных распределений.

Пусть  — случайный вектор, принимающий значения на множестве  в евклидовом пространстве, причём распределение вероятностей этого вектора принадлежит параметрическому семейству распределений, заданному плотностями , , , относительно некоторой меры . Предполагает­ся, что истинное значение параметрической точки , соответст­вующей результату наблюдений , неизвестно. Суть доверительного оценивания заключается в построении такого множества , зависящего от , которое содержит значение заданной функции , соответствующее неизвестному истинному значению параметри­ческой точки .

Пусть  — множество значений функции , , и пусть , , — какая-либо совокупность множеств, при­надлежащих  при всех  из , причём предполагается, что для произвольного элемента  и любого значения  определена вероятность события {}. Эта вероятность выражается интегралом

,, ,

и называется вероятностью накрытия множеством зна­чения  при заданном значении .

Если истинное значение  неизвестно, то множество  (из совокупности множеств , , соответствующее ре­зультату наблюдений X, называется доверительным множеством (или интервальной статистической оценкой) для неизвест­ного истинного значения функции . В качестве вероятност­ной характеристики интервальной оценки , построенной по указанному правилу, используется доверительная вероят­ность , выражающаяся в терминах вероятности накрытия равенством

, .

Иными словами  — вероятность накрытия множеством  значения заданной функции , соответствующего не­известной истинной параметрической точке .

Рекомендуемые материалы

В тех случаях, когда доверительная вероятность  от  не зависит, интервальную оценку  называют подобной пространству выборок. Это название обусловлено аналогией формул

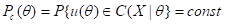
и

.

В более общей ситуации  зависит от неизвестного , и по­этому в практической работе принято характеризовать качест­во интервальной оценки коэффициентом доверия

,

где нижняя грань вычисляется на множестве  (иногда коэф­фициент доверия называется доверительным уровнем).

Оптимизация доверительного оценивания определяется теми требованиями, кото­рые предъявляются к интервальным оценкам. Например, если цель заключается в построении доверительных множеств, по­добных пространству выборок и имеющих заданный коэффи­циент доверия  (), то первое требование выражает­ся тождеством

, .

При этом естественно искать такие интервальные оценки, кото­рые накрывают истинное значение  с вероятностью, не ме­ньшей вероятности накрытия любого произвольного значения . Иными словами, второе требование, называемое требо­ванием несмещённости, выражается неравенством

, , .

В этих условиях «наилучшей» разумно считать ту интерваль­ную оценку , которая с меньшей вероятностью накрывает лю­бое значение , отличное от истинного . Отсюда возникает третье требование «наибольшей селективности»: для всякого другого доверительного множества , отличного от  и удов­летворяющего условию

, .

должно выполняться неравенство

, , .

Задача отыскания интервальных оценок , удовлетворяю­щих указанным трём требованиям, эквивалентна задаче по­строения несмещённых, наиболее мощных статистических кри­териев, подобных пространству выборок и имеющих уровень значимости . Вопросы существования решения такой за­дачи и его конструктивного описания составляют основу об­щей теории статистической проверки гипотез.

Наиболее часто применяется доверительное оценивание в ситуации, когда  — скалярная функция. Пусть , , — независимые случайные величины, подчиняющиеся одному и тому же нор­мальному распределению с неизвестными параметрами  и , причём требуется построить интервальную оценку для . Пусть

 и .

Поскольку случайная величина  подчиняется распределению Стъюдента с  степенями свободы и это распределение не зависит от неизвестных параметров  и  (,), то при любом положительном  вероятность события  зависит лишь от . Если указанный интервал принять за интервальную оценку  для , то ему будет соответствовать доверительная вероятность

,

не зависящая от . Такую интервальную оценку на­зывают доверительным интервалом, а её концевые точки — доверительными границами, или доверительными пределами, причём в данном случае доверительный интервал представляет собой интервальную оценку, подобную пространству выборок. В приведённом примере интервальная оценка является не­смещённой и наиболее селективной.

Доверительный интервал это статистическая оценка параметра вероятностного распределения, имеющая вид интер­вала, границами которого служат функции от результатов на­блюдений и который с высокой вероятностью «накрывает» не­известное значение параметра. Именно, пусть результаты на­блюдений  суть независимые случайные величины с распределением вероятностей , зависящим от числового па­раметра , где  — так называемое параметрическое множество. Тогда при фиксированном , 0<<1, интервал с границами  и ,  в параметриче­ском множестве  такой, что

,

называется доверительным интервалом для параметра  с до­верительным уровнем (коэффициентом доверия) . Здесь доверительная вероятность  вычисляется при истинном значении параметра . Границы называются доверите­льными границами, или доверительными пределами.

Пример. Пусть  есть нормальное распределение с плотно­стью вероятности

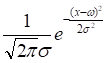
где  и  — известное число. Для построения доверительных интервалов для  рассматривается точечная статистическая оценка  параметра  и статистика , которая при любом значении  имеет стандартное нормальное распре­деление с функцией распределения

.

Поэтому для любого  вероятность

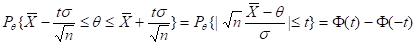
не зависит от . Для заданного  значение  находится из со­отношения

Если Вам понравилась эта лекция, то понравится и эта - История психологии.

.

Для выбранного значения  доверительный интервал

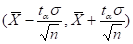
накрывает неизвестное значение  с вероятностью . Точ­ность доверительного интервала измеряется числом : вероятность ошибки, состоя­щей в том, что построенный доверительный интервал не накрывает истинное значе­ние , не превосходит . Во многих задачах удаётся найти лишь доверительный интервал, отвечающий приближённому значению доверите­льного уровня.

Понятие доверительного интервала для векторного параметра воплощается в соот­ветствующей многомерной доверительной области. Для мно­гих функциональных характеристик вероятностных распреде­лений строятся различные доверительные множества и зоны. Задача построения наилучших доверительных интервалов родственна задаче получе­ния наилучших критериев в теории проверки статистических гипотез.

Метод оценивания с помощью доверительных интервалов принадлежит Е. Нейма­ну (1935); он отличается от других методов интервального ста­тистического оценивания логической простотой и независимо­стью от априорных предположений о параметре .