Виды законов распределения вероятностей
Тема 1.5. Виды законов распределения вероятностей
Вопрсы темы:
1. Экспоненциальный закон
2. Нормальный закон
3. Закон Вейбулла
4. Закон равновероятного распределения
5. Закон Пуассона
1.5.1. Экспоненциальный закон
Экспоненциальный закон -- закон, описывающий непрерывные случайные величины, рождаемые процессом без последействия. Закон выражается формулами
Рекомендуемые материалы
интегральная функция: 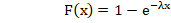
плотность распределения: 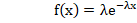
где параметром распределения является λ= 1/тх, здесь тх— математическое ожидание случайной величины.
Для случайных величин, распределенных по экспоненциальному закону, коэффициент вариации равен единице v=1 т.е. ох= тх. Формы кривых показаны на рис. 2.3.
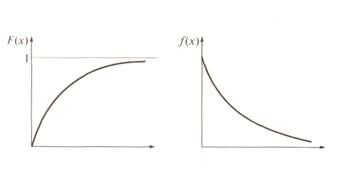
Рис. 2.3. Экспоненциальный закон распределения вероятностей
Случаи применения экспоненциального закона в практике ТЭА:
наработка на отказ автомобиля при выходе из строя различных деталей;
наработка на отказ (моменты возникновения потребности в замене) конкретной детали для группы одновременно работающих автомобилей;
периодичность внезапных отказов деталей из-за аварии и т.п. (например, прокол колеса);
время простоя автомобиля в ремонте при дефиците запасных частей.
1.5.2. Нормальный закон
Нормальный закон — описывает непрерывные случайные величины, рождаемые процессом с хорошо выраженным последействием. По предельной теореме Ляпунова, если случайная величина является суммой многих случайных величин, то она хорошо описывается нормальным законом. Отсюда можно считать, что если на процесс влияет много различных факторов, то рождаемая этим процессом случайная величина будет распределена по нормальному закону
ƒ(x) = 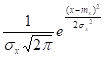
где тх — математическое ожидание случайной величины; σх - среднее квадратическое отклонение.
Интегральная функция F(х)=∫ƒ(х)dх не имеет аналитического выражения, поэтому для ее построения пользуются табличными значениями функции
F(z), где  квантиль (условный аргумент, позволяющий определять значения вероятностей для любых совокупностей нормально распределенных случайных величин). Следует отметить, что в разных литературных источниках квантиль может обозначаться различными буквами. Формы кривых распределения показаны на рис. 2.4.
квантиль (условный аргумент, позволяющий определять значения вероятностей для любых совокупностей нормально распределенных случайных величин). Следует отметить, что в разных литературных источниках квантиль может обозначаться различными буквами. Формы кривых распределения показаны на рис. 2.4.
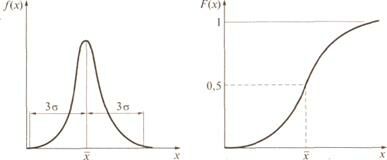
Рис.2.4.Нормальный закон распределения вероятностей
Характерной особенностью нормального закона является то, что кривая плотности вероятности симметрична относительно математического ожидания, а кривая интегральной вероятности зеркально симметрична относительно вероятности 0,5. Поскольку с вероятностью 0,997 нормально распределенная случайная величина укладывается в интервал  ± Зσ, а в реальных условиях отрицательных величин, как правило, не бывает, то математическое ожидание не может быть меньше Зσ, значит, нормально распределенные случайные величины имеют коэффициент вариации v ≤ 0,333. По этому условию выбирают вид закона распределения анализируемых случайных величин.
± Зσ, а в реальных условиях отрицательных величин, как правило, не бывает, то математическое ожидание не может быть меньше Зσ, значит, нормально распределенные случайные величины имеют коэффициент вариации v ≤ 0,333. По этому условию выбирают вид закона распределения анализируемых случайных величин.
Нормальный закон распределения вероятностей в практике ТЭА применяется при расчетах:
ресурса нормально изнашиваемых деталей;
времени простоя автомобиля в ТО и Р;
трудоемкости ТО и Р;
пробега автомобилей по календарным периодам;
расхода эксплуатационных материалов и т.п.
1.5.3. Закон Вейбулла
Закон Вейбулла — описывает непрерывные случайные величины:
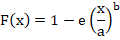
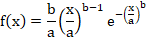
где а и b — параметры (эмпирические коэффициенты).
В зависимости от соотношения значений эмпирических коэффициентов формы кривых могут быть различны (рис. 2.5). Кривая может быть симметричной, близко совпадающей с нормальным законом, и несимметричной.
Чаще всего закон Вейбулла используют при коэффициенте вариации 0,4 ≤ v ≤ 0,9.
Закон Вейбулла в практике ТЭА применяется при расчетах:
ресурса деталей, разрушающихся из-за усталости;
наработки до отказа крепежных деталей;
простоев автомобиля в текущем ремонте и т.п.
Числовые характеристики случайной величины, распределенной по закону Вейбулла, особым образом связаны с его параметрами а и б.

Рис.2.5. Закон Вейбулла
1.5.4. Закон равновероятного распределения
Закон равновероятного распределения — описывает непрерывные случайные величины, которые достоверно встречаются на некотором интервале от и до и и вероятность наблюдения случайной величины в этом интервале постоянна (рис. 2.6).
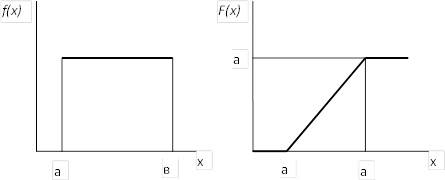
Рис. 2.6. Закон равновероятностного распределения
Описывается этот закон следующим образом:
ƒ(х) = 0 при х меньше а;
ƒ (х) = при а ≤ х ≤ b;
при а ≤ х ≤ b;
ƒ (х) = 0 при х больше а.
x - a
 при а ≤ х ≤ b;
при а ≤ х ≤ b;
Закон равновероятного распределения в практике ТЭА применяется при расчетах:
времени простоя отказавшего технологического оборудования до прихода мастера по ремонту, если заявка в течение смены обязательно выполняется;
времени ожидания маршрутного транспортного средства и т.п.
1.5.5. Закон Пуассона
Закон Пуассона — этот закон описывает дискретные случайные величины и является приближенным выражением более общего закона Бернулли. По формуле, предложенной Пуассоном, можно определять вероятность попадания в выборку п < 0,1УУ, где N — объем партии х объектов с определенным свойством, например, бракованных. При этом должно выполняться условие, что вероятность наблюдения бракованных изделий в партии должна быть не более 0,1.
Распределение выражается формулой
вероятность наступления события P(x)=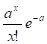
где параметр распределения является математическим ожиданием случайной величины а = тх.
Закон Пуассона в практике ТЭА применяется при определении:
числа отказов для группы одновременно работающих автомобилей в течение заданного промежутка времени (или наработки);
числа аварий или дорожно-транспортных происшествий;
числа дефектных изделий, попадающих в выборку из партии изделий;
числа клиентов, обращающихся на пункт обслуживания в единицу времени;
количества запасных частей, забираемых со склада и т.п.
Контрольные вопросы
1. Что дает более полное представление о разбросе случайной величины: среднее квадратическое отклонение или ее коэффициент вариации?
2. В чем разница между средним арифметическим и средним гармоническим значением случайной величины?
3. Почему плотность распределения вероятностей случайной величины называют дифференциальным законом распределения? Может ли этот закон описывать дискретные случайные величины?
Рекомендуем посмотреть лекцию "5 Заключение".
4. Какими законами распределения описывается наработка на отказ автомобиля и наработка до предельного износа коленчатого вала?
5. Почему нормальным законом описываются значения ресурса нормально изнашиваемых деталей автомобиля?
6. Каким законом распределения может быть описан ресурс детали, если его среднее значение в два раза больше среднего квадратического отклонения?
7. Каким законом распределения обычно описывается ресурс пружин, отказывающих из-за усталостных трещин?
8. Если известно, что в маршрутном автобусе в среднем находится 40 пассажиров, то с какой вероятностью число пассажиров будет равно10? По какой формуле это можно подсчитать?
9. В чем разница закона распределения, представленного как F(х) и ƒ(х)?






















