Метрология сигналов
Тема 2: метрология сигналов
Физическая величина более точно определяется уравнением, чем измерением.
Макс Планк (XVIII-XIX в).
(Немецкий физик - теоретик).
Теоретикам свойственно намекать о важности своих занятий. Сам себя не похвалишь, как оплеванный ходишь. Между тем, уравнение только математическая модель физической величины. А без измерений понятия точности вообще не существует.
Борис Старцев (XX в).
(Уральский геофизик - практик).
Содержание: 2.1. Пространство сигналов. Линейное пространство сигналов. Координатный базис пространства. Норма сигналов. Метрика сигналов. 2.2. Мощность и энергия сигналов. Понятия мощности и энергии сигналов. Скалярное произведение сигналов. 2.3. Обобщенный ряд Фурье. Ортогональные сигналы. Разложение сигнала в ряд Фурье. Ортонормированные системы функций. Разложение энергии сигнала. 2.4. Функции корреляции сигналов. Корреляционные функции сигналов. Взаимная корреляционная функция. Литература.
В данной теме метрология сигналов рассматривается, в основном, на уровне понятий и базовых определений, предваряя их более подробное изучение в дальнейших темах курса. Это объясняется тем, что при детальном изучении каких-либо характеристик или свойств сигналов их рассмотрение не может выполняться в отрыве от других метрологических характеристик рассматриваемых типов сигналов и требует определенной ориентировки в общей метрологии сигналов, хотя бы на уровне понятий.
Рекомендуемые материалы
2.1. Пространство сигналов [1,3,16].
Важнейшее свойство аналоговых и дискретных сигналов заключается в том, что их линейные комбинации также являются аналоговыми или дискретными сигналами. Линейные комбинации цифровых сигналов, в силу их ограничения по разрядности, в принципе относятся к разряду нелинейных операций, однако последним фактором можно пренебречь, если ошибки, которые вносятся в результаты наблюдений при квантовании отсчетов, достаточно малы по сравнению с шумами зарегистрированной информации. При дискретизации и квантовании данных непосредственно на входах в ЭВМ последнее выполняется практически всегда, поскольку ошибки определяются разрядностью ЭВМ и программными системами обработки данных, которые обычно не ниже 6-12 десятичных разрядов.
Линейное пространство сигналов. Пусть L{s1(t), s2(t), …}- множество сигналов, которые имеют какие-то общие свойства и определенную структуру связи между сигналами. Например, множество может состоять из сигналов вида sn(t) = Ancos(wnt+jn) – гармонических колебаний с определенными значениями амплитуд, частот и начальных фаз. Путем введения структурных ограничений множество сигналов может быть превращено в функциональное пространство сигналов. Так, множество сигналов L образует линейное пространство сигналов, если для него справедливы следующие аксиомы:
1. Для любых сигналов u(t) Î L и v(t) Î L существует их сумма s(t) = u(t)+v(t), которая также содержится в L, при этом операция суммирования коммутативна: u(t)+v(t) = v(t)+u(t), и ассоциативна: u(t)+(v(t)+x(t)) = (u(t)+v(t))+x(t).
2. Для любого сигнала s(t) Î L и числа a определен сигнал y(t) = as(t), у(t) Î L.
3. Множество L содержит такой нулевой элемент Æ, что для всех сигналов u(t) Î L выполняется равенство u(t)+Æ = u(t).
Сигналы могут описываться как вещественными, так и комплексными функциями, и линейные пространства также могут быть вещественными или комплексными.
Множество L, для которого выполняются данные аксиомы, при анализе сигналов и систем может рассматриваться как специальным образом сконструированное многомерное (в пределе – бесконечномерное) геометрическое пространство. Сигналы таких линейных пространств часто называют векторами в силу аналогии их свойств со свойствами векторов. Соответственно, для математического анализа систем и сигналов в линейном пространстве может использоваться математика векторов.
Пример. Множество сигналов L состоит из импульсных сигналов произвольной формы с амплитудой не более 10 вольт. Образуют ли эти сигналы линейное пространство?
Нет, не образуют, так как не выполняется, по крайней мере, первая аксиома линейного пространства (сумма двух сигналов с амплитудой более 5 вольт превышает 10 вольт). Требуются дополнительные структурные ограничения по параметрам сигналов.
Координатный базис пространства. В пространстве сигналов можно выделить координатный базис пространства - подмножество векторов {е1, е2, е3, …} со свойствами координатных осей, по которым можно разложить произвольный сигнал, принадлежащий линейному пространству.
Совокупность векторов ei пространства L является линейно независимой и образует координатный базис пространства, если равенство  aiei = Æ выполняется только в случае одновременного обращения в нуль всех числовых коэффициентов ai. При этом произвольный сигнал s(t) может быть разложен по координатному базису ei в виде
aiei = Æ выполняется только в случае одновременного обращения в нуль всех числовых коэффициентов ai. При этом произвольный сигнал s(t) может быть разложен по координатному базису ei в виде
s(t) = сiei, (2.1.1)
сiei, (2.1.1)
где числа сi – проекции сигнала s(t) на координатный базис.
Пример.
Линейное пространство образовано сигналами, которые описываются многочленом вида
s(t) = cntn.
cntn.
Координатным базисом в пространстве является система одночленов
{е0 = 1, е1 = t, e2 = t2, … , еn = tn}.
Норма сигналов. Линейное пространство сигналов L является нормированным, если каждому сигналу пространства однозначно сопоставлено число ||s(t)|| - норма (norm) сигнала, и выполняются следующие аксиомы:
1. Норма неотрицательна и равна нулю тогда и только тогда, когда сигнал равен нулю (||s(t)|| = Æ, при s(t) = Æ).
2. Для любого числа b должно быть справедливо равенство: ||bs(t)|| = |b| × ||s(t)||.
3. Если v(t) и u(t) – сигналы из пространства L, то должно выполняться неравенство треугольника: ||v(t)+u(t)|| £ ||v(t)|| + ||u(t)||.
В линейном пространстве сигналов норма является аналогом длины векторов. В математике существуют различные формы норм. Для анализа сигналов чаще всего используются квадратичные нормы:
||s(t)|| = . (2.1.2)
. (2.1.2)
Соответственно, для дискретных сигналов:
||s(t)|| = . (2.1.2')
. (2.1.2')
Для комплексных сигналов:
||s(t)|| = , (2.1.2'')
, (2.1.2'')
где s*(t) – величины, комплексно сопряженные с s(t).
Метрика сигналов. Линейное пространство сигналов L является метрическим, если каждой паре сигналов u(t) Î L и v(t) Î L однозначно сопоставляется неотрицательное число r(u(t),v(t)) – метрика (metric) или расстояние между векторами, и выполняются аксиомы:
1. r(u(t),v(t)) = r(v(t),u(t)) – рефлексивность метрики.
2. r(u(t),u(t)) = 0 для любых u(t) Î L.
3. r(u(t),v(t)) £ r(u(t),a) + r(a,v(t)) для любых a Î L.
Метрика определяется нормой разности двух сигналов:
r(u(t),v(t)) = || u(t) – v(t) ||. (2.1.3)
В свою очередь норму можно отождествлять с расстоянием от выбранного элемента пространства до нулевого: ||u(t)|| = r(u(t),Æ).
По метрике сигналов можно судить, например, о том, насколько точно один сигнал может быть аппроксимирован другим сигналом или насколько изменяется выходной сигнал относительно входного при прохождении через какое-либо устройство.
|
Рис. 2.1.1. |
Пример. Сигнал на интервале (0,Т) представляет собой половину периода синусоиды амплитудой A: s(t) = A×sin(pt/T), 0 £ t £ T. Требуется аппроксимировать сигнал прямоугольным импульсом п(t).
Если принять амплитуду импульса п(t) равной В, то квадрат расстояния между сигналами: r2(s,п) = (A sin(pt/T)-В)2 dt = A2T/2 - 4ABT/p + B2T.
(A sin(pt/T)-В)2 dt = A2T/2 - 4ABT/p + B2T.
Для решения задачи требуется найти минимум выражения r2(s,п). Дифференцируем полученное выражение по В, приравниваем нулю и, решая относительно В, находим значение экстремума: В = 2A/p » 0.64А. Это искомое значение минимума функции r2(s,п), так как вторая производная функции по В положительна. При этом минимальное значение метрики: rmin » 0.31A . Вычислим нормы сигналов при А = 1:
. Вычислим нормы сигналов при А = 1:
Еs = А2 sin2 (pt/T) dt = A2 T/2 = 10. Норма: ||s(t)|| =
sin2 (pt/T) dt = A2 T/2 = 10. Норма: ||s(t)|| = = 0.707 A
= 0.707 A » 3.16.
» 3.16.
Еп = B2 dt = B2 T » 8.1. Норма: ||п(t)|| =
dt = B2 T » 8.1. Норма: ||п(t)|| =  = B
= B » 2.85.
» 2.85.
2.2. Мощность и энергия сигналов [1,3,16].
Понятия мощности и энергии в теории сигналов не относятся к характеристикам каких-либо физических величин сигналов, а являются их количественными характеристиками, отражающими определенные свойства сигналов и динамику изменения их значений (отсчетов) во времени, в пространстве или по любым другим аргументам.
Для произвольного, в общем случае комплексного, сигнала s(t) = a(t)+jb(t), где а(t) и b(t) - вещественные функции, мгновенная мощность (instantaneous power) сигнала по определению задается выражением:
w(t) = s(t)s*(t) = [a(t)+jb(t)][(a(t)-jb(t)] = a2(t)+b2(t) = |s(t)|2, (2.2.1)
т.е. функция распределения мгновенной мощности по аргументу сигнала равна квадрату функции его модуля, для вещественных сигналов - квадрату функции амплитуд.
Энергия сигнала (также по определению) равна интегралу от мощности по всему интервалу существования или задания сигнала. В пределе:
Еs = w(t)dt =
w(t)dt = |s(t)|2dt. (2.2.2)
|s(t)|2dt. (2.2.2)
По существу, мгновенная мощность является плотностью мощности сигнала, так как измерения мощности возможны только через энергию, выделяемую на интервалах ненулевой длины:
w(t) = (1/Dt) |s(t)|2dt.
|s(t)|2dt.
Энергия сигналов может быть конечной или бесконечной. Конечную энергию имеют финитные сигналы и сигналы, затухающие по своим значениям в пределах конечной длительности, которые не содержат дельта-функций и особых точек (разрывов второго рода и ветвей, уходящих в бесконечность). В противном случае их энергия равна бесконечности. Бесконечна также энергия периодических сигналов.
Как правило, сигналы изучаются на определенном интервале Т, для периодических сигналов - в пределах одного периода Т, при этом средняя мощность (average power) сигнала:
WT(t) = (1/T) w(t) dt = (1/T)
w(t) dt = (1/T) |s(t)|2 dt. (2.2.3)
|s(t)|2 dt. (2.2.3)
Понятие средней мощности может быть распространено и на незатухающие сигналы, энергия которых бесконечно велика. В случае неограниченного интервала Т строго корректное определение средней мощности сигнала должно производиться по формуле:
Ws = 
 w(t) dt. (2.2.3')
w(t) dt. (2.2.3')
Квадратный корень из значения средней мощности характеризует действующее (среднеквадратическое) значение сигнала (root mean sqare, RMS).
Применительно к электрофизическим системам, данным понятиям мощности и энергии соответствуют вполне конкретные физические величины. Допустим, что функцией s(t) отображается электрическое напряжение на резисторе, сопротивление которого равно R Ом. Тогда рассеиваемая в резисторе мощность, как известно, равна (в вольт-амперах):
w(t) = |s(t)|2/R,
а полная выделенная на резисторе тепловая энергия определяется соответствующим интегрированием мгновенной мощности w(t) по интервалу задания напряжения s(t) на резисторе R. Физическая размерность мощности и энергии в этом случае определяется соответствующей физической размерностью функции напряжения s(t) и сопротивления резистора R. Для безразмерной величины s(t) при R=1 это полностью соответствует выражению (2.2.1). В теории сигналов в общем случае сигнальные функции s(t) не имеют физической размерности и могут быть формализованным отображением любого процесса или распределения какой-либо физической величины, при этом понятия энергии и мощности сигналов используются в более широком смысле, чем в физике. Они представляют собой специфические метрологические характеристики сигналов.
Из сравнения выражений (2.1.2) и (2.2.2) следует, что энергия и норма сигнала связаны соотношениями:
Es = ||s(t)||2, ||s(t)|| =  (2.2.4)
(2.2.4)
Пример. Цифровой сигнал задан функцией s(n) = {0,1,2,3,4,5,4,3,2,1,0,0,0,0....}.
Энергия сигнала: Es =  s2(n) = 1+4+9+16+25+16+9+4+1 = 85. Норма: ||s(n)|| =
s2(n) = 1+4+9+16+25+16+9+4+1 = 85. Норма: ||s(n)|| =  » 9.22
» 9.22
Скалярное произведение сигналов. Вычислим энергию суммы двух произвольных сигналов u(t) и v(t):
E = [u(t)+v(t)]2 dt = Eu + Ev + 2
[u(t)+v(t)]2 dt = Eu + Ev + 2 u(t)v(t) dt. (2.2.5)
u(t)v(t) dt. (2.2.5)
Как следует из этого выражения, энергии сигналов (а равно и их мощности), в отличие от самих сигналов, в общем случае не обладают свойством аддитивности. Энергия суммарного сигнала u(t)+v(t), кроме суммы энергий составляющих сигналов, содержит в себе и так называемую энергию взаимодействия сигналов или взаимную энергию:
Euv = 2 u(t)v(t) dt. (2.2.6)
u(t)v(t) dt. (2.2.6)
По аналогии с математикой векторов интеграл выражения (2.2.6) называют скалярным произведением вещественных сигналов:
Пuv = (u(t),v(t)) = u(t)v(t) dt = ||u||×||v|| cos j, (2.2.7)
u(t)v(t) dt = ||u||×||v|| cos j, (2.2.7)
Отсюда, косинус угла между сигналами:
cos j = Пuv/(||u||×||v||). (2.2.8)
Скалярное произведение обладает следующими свойствами:
1. (u,v) ³ 0;
2. (u,v) = (v,u);
3. (au,v) = a(u,v), где а – вещественное число;
4. (u+v, a) = (u,a) + (v,a).
Линейное пространство с таким скалярным произведением называется гильбертовым пространством Н (второе распространенное обозначение - L2). В нем справедливо фундаментальное неравенство Коши-Буняковского:
|Пuv| £ ||u||×||v||. (2.2.9)
Для комплексного гильбертова пространства скалярное произведение вычисляется по формуле:
Пuv = u(t)v*(t) dt. (2.2.7')
u(t)v*(t) dt. (2.2.7')
Пример. Имеется два смещенных во времени прямоугольных импульса с одинаковой амплитудой и длительностью: s1(t) = 2 при 0 £ t £ 5, s1(t) = 0 при других t; и s2(t) = 2 при 4 £ t £ 9, s2(t) = 0 при других t.
Энергии сигналов одинаковы: ||s1||2 = ||s2||2 =  s12(t)dt =
s12(t)dt = s22(t)dt = 20.
s22(t)dt = 20.
Скалярное произведение: (s1,s2) =  s1(t) s2(t) dt = 8.
s1(t) s2(t) dt = 8.
Отсюда имеем: cos j = (s1,s2)/ (||s1||×||s2||) = 8/20 = 0.4 и j » 1.16 радиан » 66о
Скалярное произведение определяет также расстояние между сигналами (метрику сигналов). Для квадрата метрики сигналов имеем:
r2(u,v) = [u(t)-v(t)]2 dt = Eu + Ev - 2×||u||×||v|| cos j.
[u(t)-v(t)]2 dt = Eu + Ev - 2×||u||×||v|| cos j.
При j = 0 (cos j = 1) сигналы "совпадают по направлению" и расстояние между ними минимально. При j = p/2 (cos j = 0) сигналы "перпендикулярны друг другу", иначе говоря - ортогональны, и проекции сигналов друг на друга равны 0. При j = p (cos j = -1) сигналы "противоположны по направлению" и расстояние между сигналами максимально. Фактор расстояния между сигналами играет существенную роль при их селекции в многоканальных системах. Если функции u(t) и v(t) являются случайными, то значение cos j играет роль коэффициента корреляции между случайными процессами U(t) и V(t).
Дискретные сигналы обычно рассматриваются в пространстве Евклида (обозначение пространства - R2). Скалярное произведение двух сигналов в пространстве Евклида - число:
Пuv = (uk,vk) = ukvk,
ukvk,
где n - размерность пространства. При n = 3 это математический прообраз реального трехмерного пространства, в котором сигналы u и v отображаются точками этого пространства.
При обработке данных используются также понятия мощности взаимодействия двух сигналов x(t) и y(t):
wxy(t) = x(t) y*(t), (2.2.10)
wyx(t) = y(t) x*(t),
wxy(t) = w*yx(t).
Для вещественных сигналов:
wxy(t) = wyx(t) = x(t) y(t). (2.2.10')
С использованием выражений (2.2.10) интегрированием по соответствующим интервалам вычисляются значения средней мощности взаимодействия сигналов на определенных интервалах Т и энергия взаимодействия сигналов.
2.3. Обобщенный ряд Фурье [1,3,11,16].
Ортогональные сигналы. Два сигнала называются ортогональными (orthogonal), если имеют нулевое скалярное произведение (и соответственно нулевую энергию взаимодействия):
Пuv = u(t)v(t) dt = 0.
u(t)v(t) dt = 0.
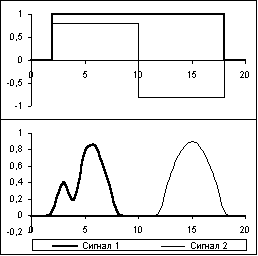
На рисунке 2.3.1 приведены примеры взаимно ортогональных сигналов. Нулевая энергия взаимодействия двух верхних сигналов обеспечивается их формой (равна нулю сумма положительных и отрицательных значений произведения сигналов), а двух нижних - взаимным расположением (ненулевые значения сигналов не имеют общих точек).
|
Рис. 2.3.1. Ортогональные сигналы. |
Из ортогональности по энергии всегда следует ортогональность сигналов по мощности, но не наоборот. Условия ортогональности по мощности и энергии выполняются одновременно только на конечных временных интервалах, при этом энергия и мощность суммы ортогональных сигналов обладают свойством аддитивности.
Совокупность функций {u0, u1, u2, …}, в пределе - бесконечную, называют системой ортогональных функций на отрезке (t1,t2), если на этом отрезке данные функции взаимно ортогональны, т.е. выполняется условие:
Пuv =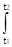 ui(t)uj(t) dt = 0, i = 1,2,..., j = 1,2,..., i ¹ j.
ui(t)uj(t) dt = 0, i = 1,2,..., j = 1,2,..., i ¹ j.
Систему ортогональных функций на интервале (t1,t2) называют ортонормированной (orthonormal functions), если все функции системы имеют единичную норму, т.е. выполняются условия:
Пuu =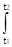 ui2(t) dt = 1, ||ui|| =
ui2(t) dt = 1, ||ui|| = = 1, i = 1,2,....
= 1, i = 1,2,....
Система ортогональных функций, для которой данное условие не выполняется, всегда может быть превращена в ортонормальную путем нормировки, т.е. деления всех функций на их норму. В линейном пространстве сигналов системы ортогональных функций могут использоваться в качестве координатных базисных функций.
Разложение сигнала в ряд Фурье. Произвольный сигнал s(t) Î H, заданный на интервале (t1,t2), может быть разложен по упорядоченной системе ортогональных базисных функций ui(t) в обобщенный ряд Фурье:
s(t) =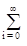 ciui(t). (2.3.1)
ciui(t). (2.3.1)
Для нахождения значений коэффициентов сi умножим обе части данного выражения на базисную функцию uk(t) с произвольным номером k и проинтегрируем результаты по переменной t, при этом получим:
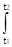 s(t)uk(t) dt =
s(t)uk(t) dt =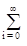 ci
ci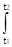 uiuk dt.
uiuk dt.
С учетом ортогональности функций u(t), в правой части этого равенства остается только один член суммы с номером i = k, который представляет собой проекцию сигнала - вектора на соответствующее базисное направление:
ck = 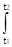 s(t)uk(t) dt. (2.3.2)
s(t)uk(t) dt. (2.3.2)
При практическом использовании количество членов ряда (2.3.1) ограничивается определенным значением N, при этом для любого значения N совокупность коэффициентов ci обеспечивают наименьшее по средней квадратической погрешности приближение к заданному сигналу.
В геометрической интерпретации коэффициенты сi представляют собой проекции вектор - сигнала s(t) на соответствующие базисные направления ui(t), т.е. координаты вектора s(t) в N-мерном пространстве (в пределе - бесконечномерном). Соответственно, энергия взаимодействия двух сигналов x(t) и y(t) может вычисляться по скалярному произведению их координатных проекций, которое равно:
Пxy = 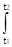 x(t)y(t) dt =
x(t)y(t) dt =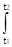
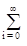 aiui(t)
aiui(t) bjuj(t)dt =
bjuj(t)dt =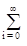 ai×bi. (2.3.3)
ai×bi. (2.3.3)
Косинус угла между векторами x(t) и y(t) с использованием выражения (2.2.8):
cos j = 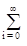 ai×bi /(||x(t)||×||y(t)||). (2.3.4)
ai×bi /(||x(t)||×||y(t)||). (2.3.4)
Возможность разложения непрерывных сигналов в обобщенные ряды Фурье имеет огромное принципиальное значение, так как позволяет вместо изучения несчетного множества точек сигнала ограничиться счетной системой коэффициентов ряда.
К системам базисных функций, которые используются при разложении сигналов, предъявляют следующие основные требования:
- для любого сигнала ряды разложения должны сходиться;
- при ограничении ряда по уровню остаточной погрешности расхождения с заданным сигналом количество членов ряда должно быть минимальным;
- функции должны иметь достаточно простую аналитическую форму;
- коэффициенты разложения должны вычисляться относительно просто.
Согласно теореме Дирехле, любой сигнал s(t), имеющий конечное число точек нарушения непрерывности первого рода и конечный по энергии на интервале (t1,t2), может быть разложен по системе ортонормальных функций, если существуют интегралы модуля сигнала и модуля его первой производной:
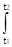 |s(t)| dt и
|s(t)| dt и 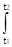 |s'(t)| dt.
|s'(t)| dt.
|
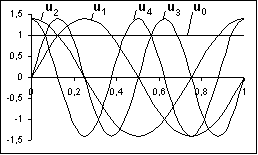
Рис. 2.3.2. Ортонормированный базис. |
Ортонормированные системы функций хорошо известны в математике. Это полиномы Эрмита, Лежандра, Чебышева, функции Бесселя, Лагерра и целый ряд других. При спектральном анализе и обработке сигналов в основном используются два вида ортонормированных функций: гармонические функции и функции Уолша.
Функции ортонормированного базиса u0,u1,u2,… на интервале [0,T], в пределе – бесконечном, на основе гармонических колебаний с кратными частотами приводятся ниже, вид первых пяти функций, включая постоянную составляющую u0, показан на рис. 2.3.2.
u0 = 1/ , uк(t) =
, uк(t) = sin(к2pt/T), uк(t) =
sin(к2pt/T), uк(t) =  cos(к2pt/T), к = 1,2,3, …
cos(к2pt/T), к = 1,2,3, …
В качестве базисных функций частотного разложения в общем случае принимаются комплексные экспоненциальные функции exp(pt) при p = jf (преобразование Фурье) и p = s+jf (преобразование Лапласа), от которых с использованием формул Эйлера
exp(jwt) = cos(wt) + j sin(wt), exp(-jwt) = cos(wt) - j sin(wt),
cos(wt) = [ехр(jwt)+exp(-jwt)]/2, sin(wt) = [ехр(jwt)-exp(-jwt)]/2j
всегда можно перейти к синус-косинусным функциям. Термин "частотного" обязан своим происхождением независимой переменной данного разложения временных сигналов, которая измеряется в единицах, обратных единицам времени, т.е. в единицах частоты f = 1/|t|. Однако понятие частотного преобразования не следует связывать только с временным представлением сигналов, т.к. математический аппарат преобразования не зависит от физического смысла переменных. Так, например, при переменной "х", как единице длины, значение f будет представлять собой пространственную частоту - число периодических изменений сигнала на единице длины с размерностью 1/|х|.
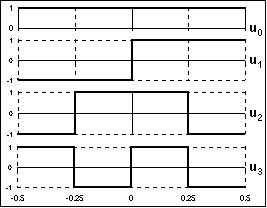
Ортонормированная система функций Уолша, по существу, является предельной модификацией системы периодических функций с кратными частотами, при этом функции принимают значения только ±1. Пример четырех первых функций Уолша на интервале Т от –0,5 до 0,5 приведен на рис. 2.3.3. Ортогональность и нормированность функций следует из принципа их построения. Стандартное математическое обозначение функций Уолша: wal(k,q), где k = 0,1,2, … – порядковый номер функции, q = t/T – безразмерная координата (нормированная на интервал Т независимая переменная).
|
Рис. 2.3.3. Функции Уолша. |
Наряду с функциями Уолша применяются также две связанные с ними системы: четные и нечетные функции cal(n,q) = wal(2n,q), – аналогичные косинусам, и sal(n,q) = wal (2n-1,q), – аналогичные синусам.
При разложении сигналов форма спектров Уолша практически тождественна спектрам гармонических функций.
Разложение энергии сигнала. Допустим, что сигнал s(t) разложен в обобщенный ряд Фурье (2.3.1). Вычислим энергию сигнала непосредственной подстановкой выражения (2.3.1) в выражение (2.2.2):
Es = s2(t) dt =
s2(t) dt =
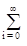
 cicjuiuj dt =
cicjuiuj dt = 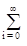
 cicj
cicj  uiuj dt. (2.3.5)
uiuj dt. (2.3.5)
В этом выражении в силу ортонормированности базисной системы отличны от нуля только члены с номерами i = j. Отсюда:
Es = s2(t) dt =
s2(t) dt =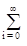 ci2, (2.3.6)
ci2, (2.3.6)
т.е. при корректном разложении сигнала в обобщенный ряд Фурье энергия сигнала не изменяется и равна сумме энергии всех составляющих ряда. Это соотношение называют равенством Парсеваля.
2.4. Функции корреляции сигналов [1, 25].
Функции корреляции сигналов применяются для интегральных количественных оценок формы сигналов и степени их сходства друг с другом.
Автокорреляционные функции (АКФ) сигналов (correlation function, CF). Применительно к детерминированным сигналам с конечной энергией АКФ является количественной интегральной характеристикой формы сигнала и представляет собой интеграл от двух копий сигнала s(t), сдвинутых относительно друг друга на время t:
Bs(t) =  s(t) s(t+t) dt. (2.4.1)
s(t) s(t+t) dt. (2.4.1)
Как следует из этого выражения, АКФ является скалярным произведением сигнала и его копии в функциональной зависимости от переменной величины значения сдвига t. Соответственно, АКФ имеет физическую размерность энергии, а при t = 0 значение АКФ непосредственно равно энергии сигнала и является максимально возможным (косинус угла взаимодействия сигнала с самим собой равен 1):
Bs(0) = s(t)2 dt = Es.
s(t)2 dt = Es.
Функция АКФ является непрерывной и четной. В последнем нетрудно убедиться заменой переменной t = t-t в выражении (2.4.1):
Bs(t) =  s(t) s(t-t) dt =
s(t) s(t-t) dt =  s(t-t) s(t) dt = Bs(-t).
s(t-t) s(t) dt = Bs(-t).
С учетом четности, вычисление АКФ обычно производится только для положительных значений t. Знак +t в выражении (2.4.1) означает, что при увеличении значений t от нуля копия сигнала s(t+t) сдвигается влево по оси t. На практике сигналы обычно также задаются на интервале положительных значений аргументов от 0-Т, что дает возможность продления интервала нулевыми значениями, если это необходимо для математических операций. В этих границах вычислений более удобным является сдвиг копии сигнала влево по оси аргументов, т.е. применение в выражении (2.4.1) функции s(t-t):
Bs(t) =  s(t) s(t-t) dt. (2.4.1')
s(t) s(t-t) dt. (2.4.1')
По мере увеличения значения величины сдвига t для финитных сигналов временное перекрытие сигнала с его копией уменьшается, а, соответственно, косинус угла взаимодействия и скалярное произведение в целом стремятся к нулю:
 = 0.
= 0.
Пример. На интервале (0,Т) задан прямоугольный импульс с амплитудным значением, равным А. Вычислить автокорреляционную функцию импульса.
 При сдвиге копии импульса по оси t вправо, при 0≤t≤T сигналы перекрываются на интервале от t до Т. Скалярное произведение:
При сдвиге копии импульса по оси t вправо, при 0≤t≤T сигналы перекрываются на интервале от t до Т. Скалярное произведение:
Bs(t) = A2 dt = A2(T-t).
A2 dt = A2(T-t).
 При сдвиге копии импульса влево, при -T≤t<0 сигналы перекрываются на интервале от 0 до Т-t. Скалярное произведение:
При сдвиге копии импульса влево, при -T≤t<0 сигналы перекрываются на интервале от 0 до Т-t. Скалярное произведение:
Bs(t) = A2 dt = A2(T+t).
A2 dt = A2(T+t).
При |t| > T сигнал и его копия не имеют точек пересечения и скалярное произведение сигналов равно нулю (сигнал и его сдвинутая копия становятся ортогональными).
 Обобщая вычисления, можем записать:
Обобщая вычисления, можем записать:
Bs(t) =  .
.
В случае сигналов с бесконечной энергией и периодических сигналов АКФ вычисляется по определенному интервалу (периоду) Т, с усреднением скалярного произведения и его сдвинутой копии в пределах этого интервала (одного периода для периодических):
Bs(t) = (1/Т) s(t) s(t-t) dt. (2.4.2)
s(t) s(t-t) dt. (2.4.2)
При t=0 значение АКФ в этом случае равно не энергии, а средней мощности сигналов в пределах интервала Т. АКФ периодических сигналов при этом также является периодической функцией с тем же периодом Т. Так, для сигнала s(t) = A cos(w0t+j0) при T=2p/w0 имеем:
Bs(t) = A cos(w0t+j0) A cos(w0(t-t)+j0) = (A2/2) cos(w0t).
A cos(w0t+j0) A cos(w0(t-t)+j0) = (A2/2) cos(w0t).
Отметим, что полученный результат не зависит от начальной фазы гармонического сигнала, что характерно для любых периодических сигналов и является одним из свойств КФ.
Взаимная корреляционная функция (ВКФ) сигналов (cross-correlation function, CCF) показывает степень сходства сдвинутых экземпляров двух разных сигналов и их взаимное расположение по координате (независимой переменной), для чего используется та же формула (2.4.1), что и для АКФ, но под интегралом стоит произведение двух разных сигналов, один из которых сдвинут на время t:
B12(t) =  s1(t) s2(t+t) dt. (2.4.3)
s1(t) s2(t+t) dt. (2.4.3)
При замене переменной t = t-t в формуле (2.4.3), получаем:
B12(t) = s1(t-t) s2(t) dt =
s1(t-t) s2(t) dt = s2(t) s1(t-t) dt = B21(-t)
s2(t) s1(t-t) dt = B21(-t)
|
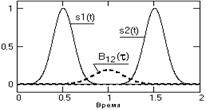
Рис. 2.4.1. Сигналы и ВКФ. |
Вместе с этой лекцией читают "Наследственность и методы ее изучения".
Отсюда следует, что для ВКФ не выполняется условие четности, а значения ВКФ не обязаны иметь максимум при t = 0. Это можно наглядно видеть на рис. 2.4.1, где заданы два одинаковых сигнала с центрами на точках 0.5 и 1.5. Вычисление по формуле (2.4.3) с постепенным увеличением значений t означает последовательные сдвиги сигнала s2(t) влево по оси времени (для каждого значения s1(t) для подынтегрального умножения берутся значения s2(t+t)).
При t=0 сигналы ортогональны и значение B12(t)=0. Максимум В12(t) будет наблюдаться при сдвиге сигнала s2(t) влево на значение t=1, при котором происходит полное совмещение сигналов s1(t) и s2(t+t). При вычислении значений B21(-t) аналогичный процесс выполняется последовательным сдвигом сигнала s1(t) вправо по временной оси с постепенным увеличением отрицательных значений t, а соответственно значения B21(-t) являются зеркальным (относительно оси t=0) отображением значений B12(t), и наоборот. На рис. 2.4.2 это можно видеть наглядно.
|
Рис. 2.4.2. Сигналы и ВКФ. |
Таким образом, для вычисления полной формы ВКФ числовая ось t должна включать отрицательные значения, а изменение знака t в формуле (2.4.3) равносильно перестановке сигналов.
Для периодических сигналов понятие ВКФ обычно не применяется, за исключением сигналов с одинаковым периодом, например, сигналов входа и выхода систем при изучении характеристик систем.