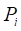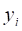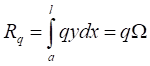Сведения из строительной механики
1. Сведения из строительной механики
1.1. Определение расчетных усилий в балках методом линий влияния
Метод линий влияния принят при расчете балок, ферм, рамных конструкций и особенно при расчете мостовых, крановых и других инженерных сооружений с подвижной нагрузкой.
Линия влияния выражает зависимость усилия (или деформации) в каком-либо заданном сечении балки или элементе фермы от положения груза на них. В практических расчетах их всегда строят от одного груза, равного единице, и после этого построения используют для определения усилий (или деформаций) в изучаемом сечении или элементе при любом заданном загружении от нескольких сосредоточенных сил или распределенных нагрузок.
Линии влияния опорной реакции в однопролетной балке с шарнирными опорами.
Линия влияния опорной реакции балки выражает зависимость величины реакции от положения груза, равного единице, на балке.
|
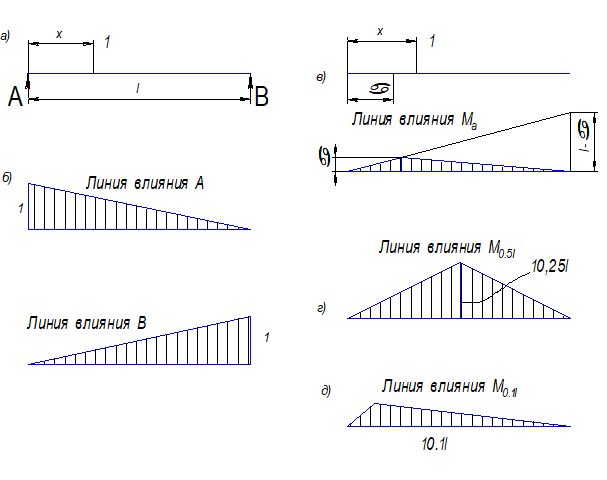
Рис. 8.1 К построению линии влияния опорных реакций и моментов в разных сечениях балки цифрами на рис д—з указаны наибольшие моменты в сечениях 0,5L, 0,4L и т д. |
Обозначим расстояние груза до левой опоры через х, пролет балки—через L (Рис. 8.1, а).
Реакция 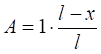
Реакция А определяется уравнением наклонной прямой (Рис. 8.1, б):
Рекомендуемые материалы
при х = 0 : А = 1:
при х = L : А = 0;
Подобным же образом строится линия влияния реакции В (Рис. 8.1, б).
Линии влияния изгибающего момента М.
Линия влияния изгибающего момента М выражает зависимость величины момента в заданном сечении от положения груза, равного единице, на балке.
Допустим, что груз находится справа на расстоянии x от опоры (Рис. 8.1, б).
При этом изгибающий момент равен:
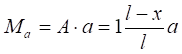
Построим линию влияния момента М (Рис. 8.1, а) из условия, что
при х = 0 : Мa = 1·а;
при х = L : Мa = 0.
Так как было сделано предположение, что груз находится справа от сечения а, то построенная прямая верна лишь на участке x≥а.
Допустим, что груз находится слева на расстоянии а от опоры.
Изгибающий момент целесообразно выразить в этом случае через величину правой опорной реакции 
где В—опорная реакция на правой опоре.
При х = 0 : Ма = 0;
при х = L : Мa = L-a.
Так как было предположено, что груз находится слева от сечения а, то построенная прямая верна лишь на участке х≤а.
Подобным образом линии влияния М строятся для разных сечений балки. Ординаты линий влияния М имеют размерность длины.
Линия влияния поперечной силы Q выражает зависимость
величины поперечной силы в заданном сечении а от положения груза, равного единице, на балке.
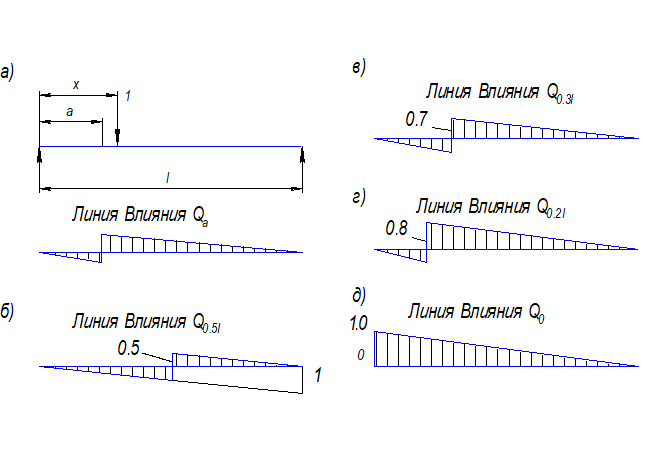
Допустим, что груз находится справа от сечения а (Рис. 8.2 , а)
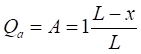
Прямая верна на участке x≥а.
Допустим, что груз находится слева от сечения а. При этом
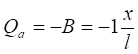
при х = 0 :  = 0;
= 0;
при х = I :  = - 1.
= - 1.
|
Рис. 8.2 К построению линий влияния поперечной силы в балках. |
Эта линия верна на участке х≤а, под исследуемым сечением она меняет знак.
Ординаты линий влияния  безразмерны.
безразмерны.
Использование линий влияния для определения усилий от системы сосредоточенных сил Р и равномерно распределенной нагрузки q.
Построенной линией влияния пользуются для определения усилия в заданном сечении балки от различной комбинации сосредоточенных и сплошных нагрузок.
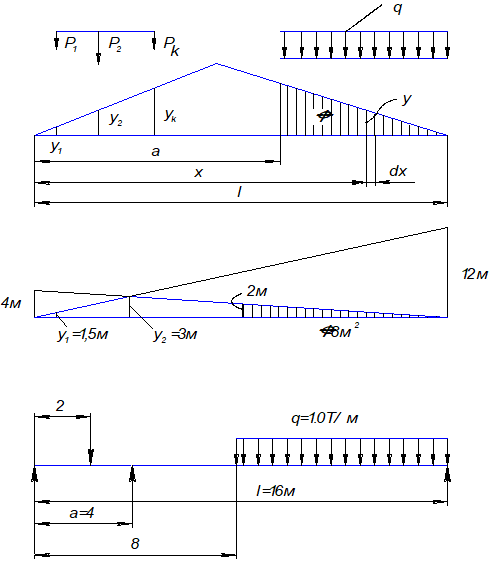
Предположим, что для сечения на расстоянии а балки построена линия влияния некоторого усилия R, имеющая вид, показанный на Рис. 8.3,а.
Балка нагружена сосредоточенными силами  ,
,  ,
,  и равномерной нагрузкой q; на участке L—а.
и равномерной нагрузкой q; на участке L—а.
|
Рис. 8.3 Определение усилий от Р и q на основе построенных линий влияния: а) общее положение; б), в) к численному примеру расчета |
Ординаты линии влияния под силами  ,
,  ,
,  обозначим соответственно
обозначим соответственно  ,
,  ,
,  .
.
Пользуясь принципом независимости действия сил, находим усилие в сечении
|
| ( 8.1) |
Усилие от равномерной нагрузки найдем, заменив сосредоточенную нагрузку бесконечно большим количеством бесконечно малых сосредоточенных сил
|
| (8.11) |
где Ω — площадь линии влияния на длине загруженного участка.
Полное усилие:
| R=ΣPiyi+qΩ | (8.12) |
R выражает собой продольную силу N, поперечную силу Q, момент М и т. д., в зависимости от построения линий влияния.
1.2. Линии влияния усилий стержневых ферм
|
Рис. 8.4 |
При загружении ферм движущимися нагрузками, например тележкой крана, целесообразно определять усилия в стержнях методом линий влияния. Линии влияния усилий стержней фермы выражают зависимость величины усилий в стержнях от положения груза, равного единице, на ферме. Таким образом, для каждого стержня фермы сроится соответствующая линия влияния.
Груз может перемещаться как по верхнему, так и по нижнему поясу фермы в соответствии с загружениями реальными силами.
По продольным брускам перемещается груз, равный единице, воспринимаемый фермой через поперечные брусья. Таким образом, осуществляется передача нагрузки на ферму по узлам.
В действительности такая надстройка нередко осуществляется в сооружениях. Если же она в действительности отсутствует, то для построения линий влияния продольных усилий поясов следует допустить, что она все же имеет место.
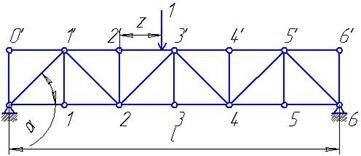
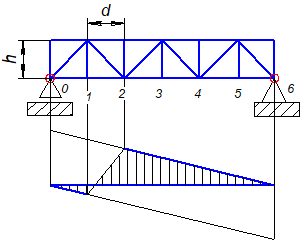
Рассмотрим линии влияния усилий в стержнях фермы с параллельными поясами, которая опирается на две опоры (Рис. 8.4, а).
Производим последовательно разрезы III - III и II - II (Рис. 8.4, б).
|
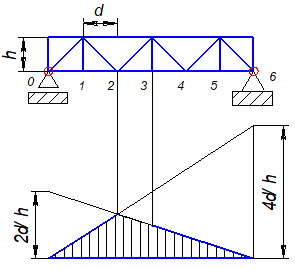
Рис. 8.5 Линия влияния усилия в стержне 23. |
Для построения линии влияния 23 рассмотрим уравнение равновесия SМ3’=0.
При грузе, находящемся справа от разрезанной панели III - III, уравнение равновесия для левой части фермы будет
A∙3d – 23 h = 0;
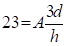
При х = 0 А =1 и 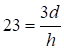
При х = l А = 0 13 = 0
Проводим правую линию влияния 23, которая верна при условии, что груз находится на участке от узла 6' до узла 3'.
При грузе, находящемся слева от разрезанной панели III - III, уравнение равновесия для правой части фермы будет
B∙3d – 32∙h = 0 откуда 
Аналогичным образом находим левую линию влияния, которая верна при грузе, находящемся на участке от узла 0' до узла 2'.
При перемещении груза от 2' до 3' линия влияния изменяется по закону прямой, изображенной на Рис. 8.5, являющейся продолжением левой линии влияния.
|
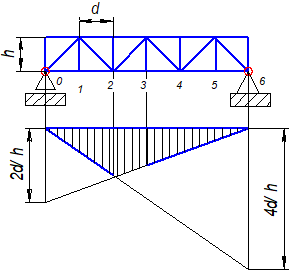
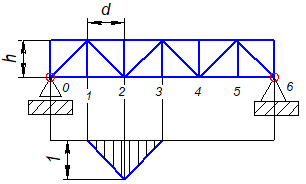
Рис. 8.6 Линия влияния усилия в стержне 2'3'. |
Аналогичным образом пишем условия равновесия SМ2=0 и строим линию влияния 2'3' (Рис. 8.6).
Если груз находится справа от 3' то 2’3’∙h+A∙2d=0 откуда 2’3’= , в т. 0’ А=Р=1, в т. 6’ А=0.
, в т. 0’ А=Р=1, в т. 6’ А=0.
Если груз находится слева от 2' то 2’3’∙h+В∙4d=0 откуда 2’3’= , в т. 6’ В=Р=1, в т. 0’ В=0.
, в т. 6’ В=Р=1, в т. 0’ В=0.
|
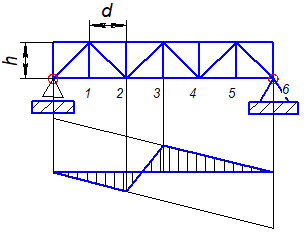
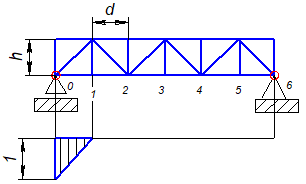
Рис. 8.7 Линия влияния усилия в стержне 23'. |
Определение усилия в раскосе 23'.
При грузе, находящемся справа от разрезанной панели, уравнение равновесия для левой части фермы запишется так:
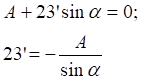
При х = 0: 23’= ;
;
При х = L: 23’ = 0
Проводим правую линию влияния 23', которая верна при грузе, находящемся на участке от узла 6' до узла 3' (Рис. 8.7).
При грузе, расположенном слева от разрезанной панели, уравнение равновесия для правой части фермы запишется так:
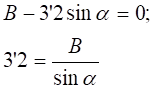
При х=0: 3’2=0
При х=l: 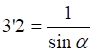
Левая линия влияния верна при грузе, находящемся на участке 0'2'.
Линия влияния 1'2' строится из рассмотрения условия равновесия узла 2'
ΣX = 0 откуда следует, что 2’1’=2’3’.
Линия влияния 0’1’ строится с учетом условия равновесия узла 0'
ΣX = 0 откуда следует, что 0’1’=0.
|
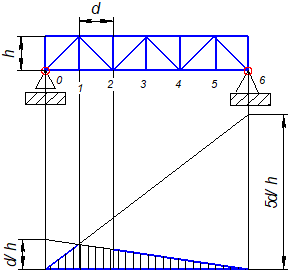
Рис. 8.8 Линия влияния усилия в стержне 12. |
Для построения линии влияния 12 проводится разрез II - II и пишутся условия равновесия ΣM1'=0.
Очертание линии влияния 12 показано на Рис. 8.8.Из условия равновесия ΣХ=0 в узле 1 следует, что линия влияния 10 равна линии влияния 12.
|
Рис. 8.9 Линия влияния усилия в стержне 1'2. |
Для построения линии влияния 1'2 следует использовать условие равновесия ΣУ=0 в сечении между 1 и 2.
При грузе, находящемся справа от разрезанной панели
A – 1’2sin α = 0
При х=0:  ;
;
при х=L: 1'2=0.
проводим правую линию влияния 1’2, которая верна при грузе, находящемся на участке от узла 6’ до узла 2' (Рис. 8.9).
При грузе, находящемся слева от разрезанной панели II – II
B + 21’ sinα = 0
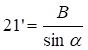
При х=L: 21’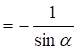
при х =0: 21’=0.
Проводим левую линию влияния на участке 0’1’. При перемещении груза от 1' до 2' линия влияния определяется уравнением прямой, изображенной на Рис. 8.9 пунктирной линией.
Аналогичным путем строим линию влияния усилия в стержне 01'.
Построим линию влияния усилия в стойке 11'
Из условия равновесия сил, приложенных в узле 1, ΣY =0 вытекает, что усилие 11'=0.
Ординаты линии влияния стойки 33' также равны нулю.
|
Рис. 8.10 Линия влияния усилия в стержне 22'. |
При построении линии влияния усилия в стержне 22' следует рассмотреть условия равновесия ΣY=0 в узле 2'.
Если груз находится вне второй и третьей панелях, то усилие 2'2=0.
Если груз находится в узле 2', то условие ΣY =0 пишется таким образом: —2'2—1=0, при этом 2'2=—1 (Рис. 8.4, и).
При перемещении груза на участках 1'2' и 23' линия влияния имеет очертание треугольника (Рис. 8.10).
|
Рис. 8.11 Линия влияния усилия в стержне 22'. |
Линия влияния усилия в опорной стойке 00' находится из условия равновесия ΣY =0 в узле 0' (Рис. 8.4, з).
При отсутствии груза на первой панели 0'0=0.
Рекомендация для Вас - Коммуникативная компетентность личности.
При нахождении груза в узле 0' уравнение равновесия запишется так:
-1-0’0 = 0 откуда 0'0 = — 1
При перемещении груза от узла 0 до узла 1 линия влияния усилия в стержне 00' определяется уравнением прямой, изображенной на Рис. 8.11 пунктирной линией.
1.3. Определение усилий в стержнях фермы при нахождении груза на поясе
Выше рассматривались случаи, когда перемещающийся груз, от которого строились линии влияния, не вызывал местного изгиба в поясе.
Допустим, что нагрузки приложены не в узлах ферм, а по длине панели. При этом нагрузки следует разложить по узлам обычным путем, от них определять продольные силы в стержнях фермы.
В нагруженных панелях помимо продольных сил действуют поперечные силы Q и изгибающие моменты М, которые определяют при рассмотрении нагруженного пояса фермы в качестве балки.



 =
=
 =Σ
=Σ