Обобщенные ряды Фурье

8 Обобщенные ряды Фурье

8.1 Сигнальное пространство

Мы уже видели, что каждая реализация измерительного сигнала x(t) является результатом чьего-то выбора (рис. 8.1) из некоторого конечного или бесконечного множества сигналов . Множество сигналов X(t), на котором определена вероятностная мера, называется ансамблем сигналов. Наличие различных реализаций в ансамбле позволяет сигналу переносить информацию о первичном сообщении.

Одним из наиболее плодотворных путей построения ансамблей сигналов считается использование методов функционального анализа – раздела математики, который обобщает наши интуитивные представления о геометрической структуре пространства.

Пусть  - множество сигналов, образующих ансамбль. Они объединены в единое множество в силу некоторых общих причин, порождающих все возможные первичные сообщения об измеряемом свойстве изучаемого объекта. Это может быть, например, множество всех непрерывных сигналов, отличных друг от друга на интервале времени 0 – T, или множество синусоидальных сигналов со случайной фазой (рис. 8.2).

Говорят, что множество сигналов наделено определенной структурой, если имеется возможность выражать одни элементы множества через другие, например, с помощью соотношения . Множество, наделенное структурой, образует пространство.

Множество М сигналов образует вещественное линейное сигнальное пространство, если для сигналов, входящих в это множество, выполняются следующие условия:

- если сигнал , то в любой момент времени он может принимать только вещественные значения,

- если  и α – вещественное число, то ,

Рекомендуемые материалы

- если, , то ,

- множество М содержит нулевой сигнал  такой, что .

Совокупность сигналов  называется линейно независимой, если равенство

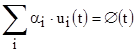
выполняется только в том случае, когда все . Совокупность линейно независимых сигналов образует координатный базис линейного сигнального пространства М и все сигналы x(t) из этого пространства могут быть представлены в виде разложения по элементам базиса:

Линейное сигнальное пространство L называется нормированным, если в нем можно ввести норму – число, которое характеризует «длину» или «величину» сигнала. Норму для сигнала x(t) будем обозначать, как . Норма должна вводиться таким образом, чтобы выполнялись аксиомы линейного нормированного пространства:

1. норма неотрицательна, то есть всегда ,

2. для любого α справедливо равенство ,

3. если , то выполняется неравенство треугольника

.

Чаще всего в качестве нормы будем использовать следующее выражение:

Это – энергетическая норма, поскольку выражение под корнем определяет энергию сигнала.

Линейное сигнальное пространство будем называть метрическим, если каждой паре сигналов  поставлено в соответствие некоторое неотрицательное число . Это число называется метрикой или расстоянием между сигналами . Метрика может быть определена по-разному, но она должна удовлетворять следующим аксиомам метрического пространства:

1.   - рефлективность метрики,

2.  ,

3.   - правило треугольника.

Обычно метрика определяется как норма разности сигналов:

.

Тогда и норму сигнала можно определить как расстояние между этим сигналом и нулевым сигналом:

.

Линейное сигнальное пространство, если на нем введена норма и метрика, называется гильбертовым пространством, если на его элементах может быть определено скалярное произведение

,

которое равно взаимной энергии сигналов. При этом должно выполняться условие Коши – Буняковского:

.

В гильбертовом сигнальном пространстве можно определить не только расстояние между сигналами, но и угол между ними

,

хотя понятие угла между сигналами не имеет наглядной геометрической интерпретации.

Пример

Сигнал x(t) – отрезок синусоиды, нормированный к единице (рис. 80):

.

Найти амплитуду В прямоугольного импульса такой же протяженности, при которой расстояние между этими двумя сигналами будет минимальным.

Для решения задачи запишем выражение для метрики как расстояния между синусоидальным сигналом и прямоугольным импульсом:

Квадрат метрики, да и сама метрика, обратится в минимум при равенстве нулю производной:

откуда следует

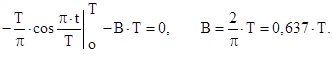
8.2 Ортогональные сигналы и обобщенные ряды Фурье

Два сигнала  в линейном гильбертовом сигнальном пространстве с метрикой и нормой называются взаимно ортогональными, если их скалярное произведение равно нулю:

.

Пусть задан некоторый ансамбль сигналов . Выбираем в сигнальном пространстве координатный базис таким образом, чтобы все базисные сигналы были попарно ортогональны на отрезке . Так выбранный базис называется системой ортогональных базисных функций . Для двух любых базисных функций из этой системы имеет место равенство:

,

где     - мощность сигнала,

          - символ Кронекера.

Система базисных функций называется ортонормированной, если все эти функции ортогональны, а их мощности равны единице. Очевидно, что любую систему ортогональных базисных функций можно сделать ортонормированной, если все эти функции поделить на корни квадратные из их мощности.

Произвольный сигнал конечной длительности  в линейном сигнальном пространстве можно представить в виде линейной комбинации ортогональных базисных функций:

.

Такое представление сигнала называется обобщенным рядом Фурье в данной системе ортогональных базисных функций.

Набор коэффициентов  образует спектр сигнала  в системе ортогональных базисных функций . Спектр полностью определяет сигнал . Во многих случаях преобразования сигналов значительно упрощаются, если их проводить не над самими сигналами, а над их спектрами в специально выбранных системах базисных функций. Поскольку спектр состоит из набора чисел, то для проведения самых различных преобразований можно использовать средства цифровой вычислительной техники.

Для определения j-го спектрального коэффициента  следует вычислить скалярное произведение сигнала с соответствующей базисной функцией :

Отсюда следует, что спектральные коэффициенты  сигнала  в системе ортогональных базисных функций  должны определяться как

При представлении сигнала в системе ортогональных базисных функций всегда приходится ограничиваться некоторым конечным числом N членов ряда. Получаемый при этом сигнал

называется аппроксимирующим рядом. Погрешность аппроксимации

характеризуется дисперсией погрешности, равной

.

Представление сигнала в виде обобщенного ряда Фурье по системе ортогональных базисных функций замечательно тем, что по мере увеличения числа N аппроксимирующего ряда погрешность аппроксимации всегда только уменьшается. При  имеет место  и тогда . При этом аппроксимирующий ряд становится бесконечным – обобщенным рядом Фурье.

Для обобщенного ряда Фурье справедливо равенство Парсеваля:

Это еще раз подчеркивает математическое равноправие двух форм представления сигнала: сигнала в виде функции времени  и сигнала в виде спектра . Левая часть равенства Парсеваля – это мощность сигнала, как функции времени, правая часть равенства – это мощность сигнала, представленного своим спектром.

Таким образом, обобщенный ряд Фурье для сигнала  на конечном интервале времени T в ортогональной системе базисных функций  имеет вид:

                  сигнал в форме ряда Фурье,

        спектр сигнала,

                   равенство Парсеваля.

Если ряд Фурье ограничен конечным числом N членов ряда, то равенство Парсеваля нарушается и средняя квадратическая погрешность (стандартное отклонение погрешности) приближения сигнала  конечным рядом  составляет .

По итогам рассмотренных положений можно сделать следующие выводы.

1. Обобщенный ряд Фурье позволяет представить любую реализацию случайного сигнала из данной реализации как сумму произведений детерминированных функций времени на систему соответствующим образом выбранных спектральных коэффициентов.

2. На множестве реализаций случайного сигнала спектральные коэффициенты являются случайными величинами. Система случайных спектральных коэффициентов как система случайных величин описывается

o вектором математических ожиданий спектральных коэффициентов,

o вектором дисперсий спектральных коэффициентов,

o матрицей моментов взаимной корреляции спектральных коэффициентов.

3. Множество сигналов  из ансамбля  имеет мощность континуума. Множество спектральных коэффициентов является, по крайней мере, счетным. Это значительно упрощает анализ случайных сигналов, заданных в форме спектр.

4. Спектральные коэффициенты могут служить информативными параметрами сигнала.

5. Система ортогональных базисных функций определяет каноническое разложение случайного сигнала, если спектральные коэффициенты для данного ансамбля являются случайными некоррелированными величинами.

Определенный интерес имеет рассмотрение двух следующих вопросов:

- выбрать, исходя из некоторых свойств ансамбля реализаций случайного сигнала, систему ортогональных базисных функций таким образом, чтобы совокупность спектральных коэффициентов была не коррелированной,

- отыскать такую систему ортогональных базисных функций, в которой последовательность спектральных коэффициентов наиболее быстро убывает с ростом индекса спектрального коэффициента.

8.3 Системы ортогональных базисных функций

В сигнальном пространстве можно построить различные системы ортогональных базисных функций. Однако спектральному анализу сигналов в различных системах функций соответствует различная интерпретация результатов и различная техническая реализация средств информационно – измерительной техники. Поэтому имеет смысл рассмотреть и сравнить друг с другом различные системы ортогональных базисных функций.

8.3.1 Система тригонометрических базисных функций

Система тригонометрических базисных функций имеет следующий вид:

Построенная таким образом система функций является ортонормированной на интервале  и ее использование приводит нас к разложению сигналов по обыкновенным тригонометрическим рядам Фурье.

8.3.2 Система полиномов Лежандра

Полиномы Лежандра порядка n вычисляются как производные:

Полиномы Лежандра порядков с 0-го до 6-го выражаются следующими формулами:

Полиномы не совпадающих друг с другом порядков попарно ортогональны и имеют мощность

,

поэтому соответствующие ортонормированные полиномы Лежандра принимают следующий вид:

На рис. 8.4 представлены графики первых семи полиномов Лежандра после их деления на корень квадратный из мощности, то есть после ортонормирования, включая и полином нулевого порядка. Они отличаются от полиномов Чебышева только тем, что их максимумы увеличиваются к концам диапазона, в остальном они ведут себя похожим образом.

Полиномы Лежандра замечательны тем, что среди всех других полиномов данной степени с одинаковым старшим членом они имеют наименьшее среднее квадратическое отклонение от нуля.

Если измерительный сигнал  задан на интервале 0<t<T, то система полиномов Лежандра приводится к этому интервалу подстановкой

.

Наоборот, сам сигнал перед разложением в ряд по полиномам Лежандра можно привести к интервалу –1<τ<+1 с помощью подстановки

.

Поэтому спектральные коэффициенты разложения сигнала  на интервале 0<t<T в обобщенный ряд Фурье по полиномам Лежандра вычисляются как:

Пример

Сигнал  представляет собой отрезок синусоиды на интервале 0<t<T, где T=0,01 с – период колебаний:

.

После замены переменных  был произведен расчет спектра сигнала  по полиномам Лежандра:

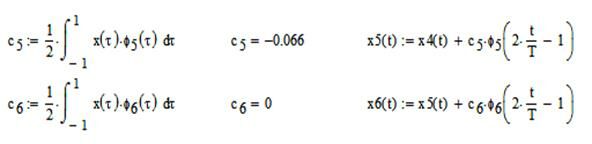
Таким образом, спектр сигнала имеет вид:

На рис. 8.5 представлен сам исходный сигнал  и суммы первых двух, четырех и шести членов разложения в ряд Фурье по полиномам Лежандра. Если сумма двух членов разложения (прямая линия) еще существенно отличается от исходного сигнала, то сумма четырех членов дает вполне приличное приближение. Ряд Фурье из шести членов практически полностью совпадает с сигналом, так что различия на глаз уже не различимы. Погрешность представления сигнала  рядом Фурье с шестью членами в виде их
разности представлена на рис. 8.6.

Из графика на рис. 8.6 видно, что погрешность только на концах диапазона немного превышает сотую долю амплитуды сигнала. Для сравнения на рис. 8.7 представлены графики того же самого сигнала  и его представление в виде степенного ряда Тейлора с шестью членами разложения, то есть тоже в виде полинома шестой степени. Ясно видно, что если в середине диапазона приближение вполне приличное, то на концах диапазона различие уже достигает половины амплитуды.

8.3.3 Системы базисных функций Уолша

Базисные функции систем Уолша отличаются тем, что имеют форму прямоугольных колебаний и принимают только значения, равные ±1. По этой причине функции системы Уолша наиболее просто реализуются средствами цифровой вычислительной техники. Основой построения систем базисных функций Уолша являются функции Радемахера  с интервалом определения . Функции Радемахера определяются следующим образом:

Здесь sign(x) – функция знака, принимающая значения +1 или –1 в зависимости от знака аргумента.

При построении функции Радемахера порядка k интервал ее определения 0 – 1 разбивается на  подинтервалов и на каждом из них функция Радемахера принимает значение +1 или –1. Первые шесть функций Радемахера представлены на рис. 8.8. На концах интервалов имеют место разрывы первого порядка, причем в точках разрыва функции Радемахера считаются непрерывными справа.

Система функций Радемахера является ортонормированной, но она не полна, поскольку можно обнаружить функции, например , не входящие в эту систему, но ортогональные всем функциям этой системы. Такие функции не могут быть представлены разложением в обобщенный ряд Фурье по системе функций Радемахера, поскольку все спектральные коэффициенты обратятся в нуль. Дополняя систему функций Радемахера их различными произведениями, можно построить несколько полных систем базисных функций, которые называются системами базисных функций Уолша. К ним относятся системы ортонормированных базисных функций Пэли, Адамара, Хармута и ряд других.

Система Уолша – Пэли отличается тем, что получаемые в ней спектры широкого класса непрерывных сигналов сходятся быстрее всего, то есть спектральные коэффициенты убывают наиболее быстро с ростом номера коэффициента. В системе Уолша – Пэли каждая базисная функция Уолша с номером i равна произведению функций Радемахера с номерами, совпадающими с номерами двоичных разрядов в двоичном представлении числа i, содержащих единицу. Если n – разрядное двоичное представление числа i имеет вид:

,

где k – номер разряда, начиная с младшего, то функция Уолша с номером i должна быть записана в виде:

.

Так, например, шестая функция Уолша (6 = LL0) определяется как

.

Порядок ее определения представлен на рис. 8.9. Если номер i является степенью числа 2, то двоичное представление числа i содержит только одну единицу, и соответствующая функция Уолша совпадает с одной из функций Радемахера.

На рис 8.10 представлены графики функций Уолша – Пэли до шестого порядка включительно.

Ряд Фурье – Уолша для сигнала ,  имеет вид:

, а спектр Уолша .

Ограничиваясь конечным числом членов разложения в ряд, мы получаем приближенное выражение для исходного сигнала.

Пример

В лекции "8 Качество говядины и факторы, на нее влияющие" также много полезной информации.

Найти спектр Уолша и аппроксимирующий ряд из семи членов разложения в ряд Фурье – Уолша сигнала  на промежутке времени , где T=0,1 c.

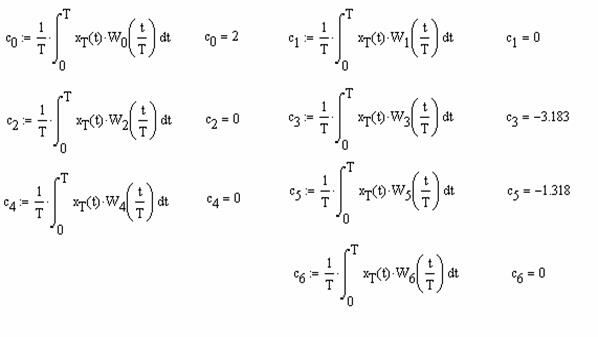
Расчет спектра Уолша:

Спектр Уолша для данного сигнала имеет вид:

.

Аппроксимирующий ряд из первых семи членов, включая нулевой, составляет:

На рис. 8.11 изображены графики сигнала  и аппроксимирующего ряда . На рисунке четко виден характер приближения измерительного сигнала рядом Фурье – Уолша. Основная особенность заключается в том, что исходный аналоговый сигнал заменяется ступенчатой линией, которая вьется вокруг сигнала.