Случайные сигналы
4. Случайные сигналы
Случайными или стохастическими называются сигналы, конкретную форму протекания которых предсказать заранее невозможно. Можно лишь с определенными вероятностями предсказать диапазоны, в которых эти сигналы будут находиться в определенные моменты времени. Все характеристики таких сигналов являются статистическими, то есть имеют вероятностный характер. В информационно-измерительной технике встречаются два вида сигналов, нуждающихся в вероятностном описании.
Во-первых, это шумы – хаотически изменяющиеся во времени колебания, генерируемые самими устройствами измерительной информационной системы или возникающие в результате воздействия внешних факторов. Шумы накладываются на сигналы, переносящие измерительную информацию, и приводят к увеличению неопределенности результатов измерений. Во-вторых, это все сигналы, несущие информацию, поэтому для описания закономерностей, присущих осмысленным сообщениям, приходится прибегать к вероятностным методам.
4.1 Модели случайных сигналов
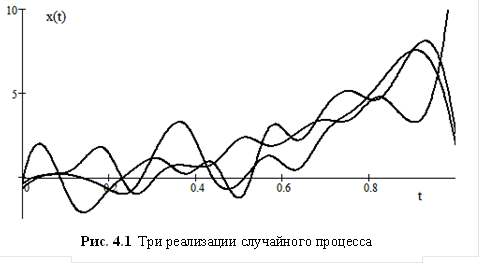
Математической моделью случайного сигнала является случайный процесс. Случайный процесс – это функция особого рода, отличающаяся тем, что ее значения в любой момент времени являются случайными величинами. До момента регистрации или приема случайный сигнал нужно рассматривать как бесконечную совокупность возможных реализаций, так называемый ансамбль реализаций, подчиняющийся некоторой общей для него статистической закономерности.
На рис 4.1 представлено несколько таких реализаций одного случайного процесса. Будучи зафиксированными, эти реализации становятся уже детерминированными сигналами.
В дальнейшем будем обозначать случайный сигнал как ансамбль возможных реализаций большими буквами X(t), Y(t) а их отдельные реализации – малыми буквами x(t), y(t), так что сигнал x(t) является реализацией случайного сигнала X(t):  .
.
Математическая модель случайного сигнала может представлять собой в простейшем случае описание всех его возможных реализаций с указанием вероятностных характеристик частоты их появления. Сейчас мы рассмотрим несколько таких моделей сигналов.
1. Гармонический сигнал со случайной начальной фазой.
Рекомендуемые материалы
Это сигнал с определенной амплитудой и частотой, но случайной начальной фазой, что связано со случайностью момента начала приема или передачи такого сигнала:

В большинстве случаев начальную фазу можно считать распределенной равномерно в диапазоне от 0 до 2π или от –π до +π, так что плотность ее распределения составляет:
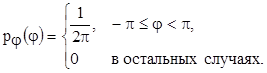
Математическое ожидание случайной фазы в этом случае равно нулю  , дисперсия - одной двенадцатой части интервала ее
, дисперсия - одной двенадцатой части интервала ее
 |
распределения
 , а стандартное отклонение фазы определяется как корень квадратный из дисперсии
, а стандартное отклонение фазы определяется как корень квадратный из дисперсии  . На рис. 4.2 представлены четыре реализации одного случайного процесса, отличающиеся значениями начальной фазы.
. На рис. 4.2 представлены четыре реализации одного случайного процесса, отличающиеся значениями начальной фазы. Вообще то сигналы такого рода мы отнесли ранее к классу квазидетерминированных сигналов.
2. Случайный телеграфный сигнал
Телеграфным называется сигнал, реализации которого могут принимать только два значения +1 или –1, причем переходы от –1 к +1 или наоборот происходят в случайные моменты времени. Число N переходов, происходящих за время τ, является случайной целочисленной величиной, дискретное распределение вероятностей которого подчиняется закону Пуассона:
 .
.
Параметр распределения λ>0 – неотрицательное число с размерностью частоты, которое и определяет среднюю частоту перепадов уровня сигнала.
 Скачки уровня сигнала происходят в случайные моменты времени, поэтому невозможно дать аналитическое описание даже одной реализации сигнала. График для реализации можно изобразить так, как это представлено на рис. 4.3. В данном случае конкретная реализация задается бесконечным множеством одинаково распределенных случайных величин – моментов возникновения перепадов уровня сигнала. Характеристики случайного процесса определяются статистическими свойствами этих случайных величин.
Скачки уровня сигнала происходят в случайные моменты времени, поэтому невозможно дать аналитическое описание даже одной реализации сигнала. График для реализации можно изобразить так, как это представлено на рис. 4.3. В данном случае конкретная реализация задается бесконечным множеством одинаково распределенных случайных величин – моментов возникновения перепадов уровня сигнала. Характеристики случайного процесса определяются статистическими свойствами этих случайных величин.
 Более общими являются модели случайных сигналов, основанные на использовании многомерных плотностей распределения.
Более общими являются модели случайных сигналов, основанные на использовании многомерных плотностей распределения.
На рис.4.4 представлены три реализации случайного процесса, который мы назовем «процесс изменения температуры в холодильнике после его отключения от сети». Три реализации соответствуют трем холодильникам. Можно считать, что всем холодильникам данного типоразмера свойственны похожие реализации этого процесса. Это объясняется единством механизма, порождающего данный процесс. Для холодильников другого типоразмера и другого завода – изготовителя множество таких реализаций может носить совершенно другой характер и должны быть отнесены к другому процессу.
Таким образом, множество реализаций может быть множеством реализаций одного или нескольких различных случайных процессов и нам нужно найти такой способ описания случайных процессов, который позволил бы отличать их друг от друга и давать некоторую информацию о механизме формирования их реализаций.
Наряду с множеством реализаций  данного случайного сигнала X(t) введем понятие множества сечений случайного сигнала
данного случайного сигнала X(t) введем понятие множества сечений случайного сигнала  .
.
Под сечением случайного сигнала будем понимать множество значений, которые принимают различные реализации сигнала в один и тот же момент времени  . Эти значения можно считать реализациями случайной величины
. Эти значения можно считать реализациями случайной величины  . Таким образом, значения случайного сигнала в любой момент времени
. Таким образом, значения случайного сигнала в любой момент времени  являются случайными величинами, зависящими от времени. Зависимость от времени проявляется как зависимость от времени плотности распределения этой случайной величины и, следовательно, таких числовых характеристик как математическое ожидание или дисперсия. Более тонкая структура случайного сигнала описывается многомерными плотностями распределения.
являются случайными величинами, зависящими от времени. Зависимость от времени проявляется как зависимость от времени плотности распределения этой случайной величины и, следовательно, таких числовых характеристик как математическое ожидание или дисперсия. Более тонкая структура случайного сигнала описывается многомерными плотностями распределения.
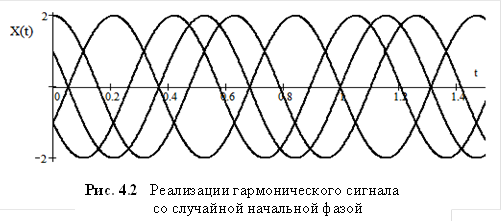
1. Одномерную плотность распределения случайного сигнала в сечении  будем обозначать
будем обозначать  , где буква
, где буква  символизирует те значения, которые могут принимать отдельные реализации случайного сигнала в момент времени
символизирует те значения, которые могут принимать отдельные реализации случайного сигнала в момент времени  . Это говорит о том, что плотность распределения является теперь функцией времени. Через плотность распределения определяются вероятности типа
. Это говорит о том, что плотность распределения является теперь функцией времени. Через плотность распределения определяются вероятности типа
 ,
,
то есть бесконечно малые вероятности события, заключающегося в том, что в момент времени  случайный сигнал
случайный сигнал  примет некоторое значение
примет некоторое значение  , лежащее в бесконечно малом интервале от
, лежащее в бесконечно малом интервале от  до
до  . С помощью этих элементарных вероятностей можно вычислить интервальные вероятности – вероятности того, что случайный сигнал в момент времени
. С помощью этих элементарных вероятностей можно вычислить интервальные вероятности – вероятности того, что случайный сигнал в момент времени  примет некоторое значение в интервале от
примет некоторое значение в интервале от  до
до  :
:
 .
.
Плотность распределения позволяет определить числовые характеристики сечений случайного процесса – его математическое ожидание и дисперсию:
 В этих двух выражениях индекс j можно опустить и считать, что математическое ожидание и дисперсия случайного сигнала в отличие от случайной величины зависят от времени.
В этих двух выражениях индекс j можно опустить и считать, что математическое ожидание и дисперсия случайного сигнала в отличие от случайной величины зависят от времени.
Плотность нормального распределения приходится теперь записывать в виде:
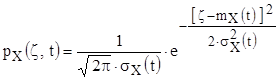
В примере на рис. 37 математическое ожидание сигнала как мера середины зоны рассеивания реализаций растет, причем этот рост экспоненциально затухает со временем, а дисперсия как мера рассеивания реализаций относительно математического ожидания со временем уменьшается.
Зная математическое ожидание и дисперсию сигнала, можно построить изменяющуюся во времени зону возможных значений сигнала
 .
.
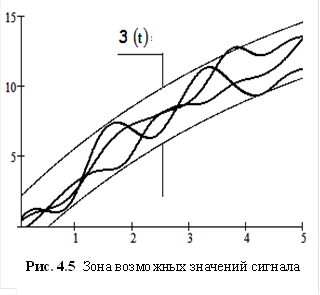
 Внутри этой зоны значения сигнала распределены случайно в соответствии с особенностями плотности распределения. Коэффициент
Внутри этой зоны значения сигнала распределены случайно в соответствии с особенностями плотности распределения. Коэффициент  зависит от выбора доверительной вероятности Р – вероятности того, что в каждый данный момент времени реализация остается в пределах этой зоны. Для нормально распределенного случайного процесса
зависит от выбора доверительной вероятности Р – вероятности того, что в каждый данный момент времени реализация остается в пределах этой зоны. Для нормально распределенного случайного процесса  при доверительной вероятности P=95 %.
при доверительной вероятности P=95 %.
На рис. 4.5 показаны для примера три реализации случайного сигнала и зона его возможных значений. Одна из реализаций вышла вниз за пределы зоны. Это сработали те самые 5 %, которых не достает доверительной вероятности Р=95 % до 100 %.
В качестве экспериментальной оценки (точечной оценки, приближенного значения) для математического ожидания и дисперсии по полученным в эксперименте N значениям N реализаций сигнала X(t) в каждом конкретном сечении  используют среднее значение сигнала и его стандартное отклонение
используют среднее значение сигнала и его стандартное отклонение
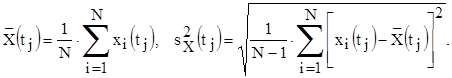
Индекс j у моментов времени здесь так же можно опустить.
2. Двухмерную плотность распределения случайного сигнала  в двух произвольных сечениях
в двух произвольных сечениях  и
и  обозначим
обозначим  . Двухмерная плотность позволяет определить элементарные вероятности типа
. Двухмерная плотность позволяет определить элементарные вероятности типа
 Это вероятности событий, заключающихся в том, что реализация случайного сигнала в сечении
Это вероятности событий, заключающихся в том, что реализация случайного сигнала в сечении  , приняв некоторое значение
, приняв некоторое значение  , лежащее в бесконечно узком интервале от
, лежащее в бесконечно узком интервале от  до
до  в сечении
в сечении  примет значение
примет значение  , лежащее в бесконечно узком интервале от
, лежащее в бесконечно узком интервале от  до
до  .
.
Теперь совместная вероятность того, что в сечении  реализация случайного сигнала примет значение
реализация случайного сигнала примет значение  , лежащее между
, лежащее между  , а в сечении
, а в сечении  - значение
- значение  , лежащее между
, лежащее между  , определится как
, определится как
 .
.
Двухмерная плотность одна определяет значения двух математических ожиданий и двух дисперсий сразу в двух сечениях случайного сигнала  и
и  :
:
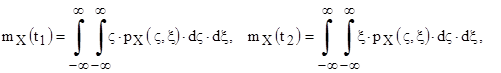
 и отсюда вроде бы следует, что двухмерная плотность не дает никаких других сведений о структуре случайного сигнала кроме тех, которые содержатся в одномерной плотности.
и отсюда вроде бы следует, что двухмерная плотность не дает никаких других сведений о структуре случайного сигнала кроме тех, которые содержатся в одномерной плотности.
На самом же деле здесь появляется возможность построения еще одной интересной характеристики случайного сигнала – его корреляционной функции
 .
.
Корреляционная функция характеризует степень тесноты, близости связи между значениями сигнала в двух его любых сечениях  и
и  к некоторой функциональной связи.
к некоторой функциональной связи.
 Для большей иллюстративности этого свойства корреляционной функции вводится понятие нормированной корреляционной функции или коэффициента корреляции Пирсона между сечениями. Коэффициент корреляции получается делением корреляционной функции на произведение стандартных отклонений в соответствующих сечениях:
Для большей иллюстративности этого свойства корреляционной функции вводится понятие нормированной корреляционной функции или коэффициента корреляции Пирсона между сечениями. Коэффициент корреляции получается делением корреляционной функции на произведение стандартных отклонений в соответствующих сечениях:
 .
.
Коэффициент корреляции Пирсона может принимать значения из интервала от –1 до +1. При корреляции, близкой к –1 или +1 значения, принимаемые реализацией случайного сигнала в двух сечениях, тесно взаимосвязаны.
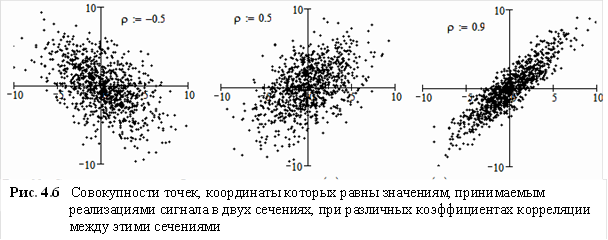
На рис 4.6 представлены три совокупности из 1000 значений, принимаемых тысячей реализаций трех случайных сигналов в двух сечениях при различных коэффициентах корреляции, но одинаковых одномерных плотностях распределения в этих сечениях. Абсцисса каждой точки – это значение, принимаемое одной из тысячи реализаций случайного сигнала в сечении  . Ее ордината – это значение, принимаемое той же реализацией в сечении
. Ее ордината – это значение, принимаемое той же реализацией в сечении  . При малых коэффициентах корреляции ρ=0,5 или ρ=-0,5 зависимость между этими значениями очень слабая, при ρ=0,9 – достаточно сильная, чтобы можно было с уверенностью утверждать – чем больше
. При малых коэффициентах корреляции ρ=0,5 или ρ=-0,5 зависимость между этими значениями очень слабая, при ρ=0,9 – достаточно сильная, чтобы можно было с уверенностью утверждать – чем больше  по сравнению с математическим ожиданием в этом сечении, тем большим будет и
по сравнению с математическим ожиданием в этом сечении, тем большим будет и  по сравнению с математическим ожиданием во втором сечении.
по сравнению с математическим ожиданием во втором сечении.
Если моменты времени  обозначить через
обозначить через  , где
, где  , а τ считать расстоянием по времени между сечениями, то корреляционную функцию можно записать в виде
, а τ считать расстоянием по времени между сечениями, то корреляционную функцию можно записать в виде  . Так записанная корреляционная функция обладает следующими очевидными свойствами:
. Так записанная корреляционная функция обладает следующими очевидными свойствами:
- для совпадающих сечений t=s, то есть при τ=0, корреляционная функция равна дисперсии этого сечения
 ,
,
- при любом расстоянии τ между сечениями имеет место соотношение
 ,
,
- при увеличении расстояния между сечениями корреляционная функция убывает до нуля
 ,
,
- корреляционная функция является четной функцией расстояния между сечениями
 .
.
Случайный сигнал называется нормальным или гауссовым, если двухмерная плотность его распределения для двух любых сечений процесса, разделенных интервалом протяженностью τ, описывается выражением:
 Окончательно по этому разделу можно сделать следующие выводы:
Окончательно по этому разделу можно сделать следующие выводы:
1. Одномерное распределение значений сигнала позволяет определить две числовые характеристики сигнала – его математическое ожидание и дисперсию. Зависимость математического ожидания от времени характеризует в среднем форму развитие сигнала во времени. Дисперсия дает информацию о том, насколько значения отдельных реализаций сигнала в каждом сечении отличаются от соответствующих математических ожиданий.
2. Двухмерная плотность распределения позволяет определить еще одну характеристику сигнала – его корреляционную функцию. Корреляционная функция как функция двух моментов времени определяет степень тесноты зависимости значений, принимаемых реализациями сигнала в одном сечении, от значений, принимаемых ими в другом сечении. Быстрое затухание корреляционной функции с ростом расстояния между сечениями говорит о быстром затухании этой зависимости, о быстрой изменчивости реализаций, о широком частотном спектре сигнала. Наоборот, медленное затухание корреляционной функции свидетельствует о плавности отдельных реализаций сигнала, о малой протяженности его частотного диапазона.
4.2 Стационарные случайные сигналы
Материал предыдущего раздела позволяет сделать вывод о том, что случайный сигнал можно представить себе в виде суммы двух составляющих:
- относительно медленно изменяющееся во времени математическое ожидание сигнала  , характеризующее развитие сигнала в среднем,
, характеризующее развитие сигнала в среднем,
- относительно быстро изменяющийся во времени центрированный случайный сигнал  , структура которого определяется поведением корреляционной функции
, структура которого определяется поведением корреляционной функции  .
.
 На рис. 4.7 представлены три реализации случайного сигнала (верхний график) и его разложение на две составляющие.
На рис. 4.7 представлены три реализации случайного сигнала (верхний график) и его разложение на две составляющие.
Одна составляющая представляет собой медленно изменяющийся процесс, изображенный на среднем графике. Это – математическое ожидание сигнала, относительно которого флуктуируют его отдельные реализации.
 На нижнем графике (в увеличенном масштабе) изображено то, что осталось от реализаций сигнала после вычитания из них математического ожидания. Эти кривые, казалось бы, беспорядочно флуктуируют относительно нуля, но в тоже время подчиняются некоторой общей закономерности, описываемой корреляционной функцией сигнала.
На нижнем графике (в увеличенном масштабе) изображено то, что осталось от реализаций сигнала после вычитания из них математического ожидания. Эти кривые, казалось бы, беспорядочно флуктуируют относительно нуля, но в тоже время подчиняются некоторой общей закономерности, описываемой корреляционной функцией сигнала.
Именно эта разновидность случайных сигналов и заслуживает более внимательного рассмотрения, поскольку как раз в ней сосредоточено то, что делает сигнал случайным.
Случайный сигнал называется стационарным, если его математическое ожидание равно нулю, а корреляционная функция зависит только от одного аргумента – расстояния между сечениями:
 .
.
Такие сигналы имеют форму относительно быстрых или медленных колебаний относительно нулевого уровня. Реализации сигнала протекают равномерно во времени, так что начало отсчета времени не имеет значения. Они обладают бесконечной энергией, но конечной мощностью, равной дисперсии сигнала. Чем быстрее затухает корреляционная функция с ростом расстояния между сечениями сигнала, тем быстрее флуктуируют относительно среднего отдельные реализации сигнала. Чем положе протекает корреляционная функция, тем более гладкими являются и реализации сигнала.
Корреляционная функция случайного стационарного сигнала обладает следующими свойствами:
- при аргументе, равном нулю, корреляционная функция принимает значение, равное дисперсии (мощности) сигнала
 ,
,
- при любом значении аргумента τ значение нормированной корреляционной функции
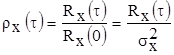
- равно коэффициенту корреляции между сечениями случайного сигнала, расположенными на расстоянии τ друг от друга,
- при любом τ значение корреляционной функции удовлетворяет условию
 ,
,
- для реально наблюдаемых случайных сигналов при больших расстояниях между сечениями значение корреляционной функции убывает до нуля
 ,
,
- корреляционная функция является четной по своему аргументу
 ,
,
поэтому имеет смысл графически изображать только часть корреляционной функции, соответствующую положительным значениям τ.
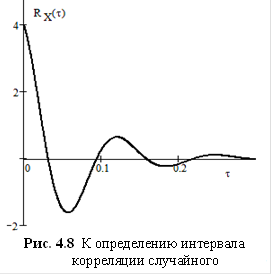
Промежуток времени, в течение которого корреляционная функция убывает до 5% или 10% от своего начального значения, называется интервалом или временем корреляции случайного сигнала.
 |
Для сигнала, корреляционная функция которого изображена на рис. 4.8, интервал корреляции можно принять равным 0,2 секунды. В границах этого интервала сигнал еще как-то «помнит» свои предыдущие значения. Этот факт находит свое выражение в характере протекания его отдельных реализаций, однако уже через 0,2 с сигнал полностью «забывает» свою предысторию и его значения в сечениях, отстоящих друг от друга на большие интервалы времени, уже никак не связаны друг с другом.
Если стационарный сигнал является к тому же и нормальным (гауссовым) сигналом, то его двухмерная плотность распределения имеет вид:
 .
.
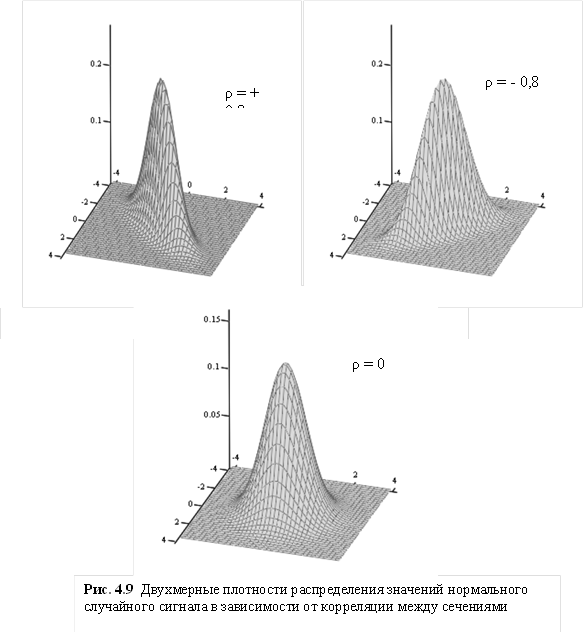
На рис. 4.9 представлены формы поверхностей, заданных этим уравнением при значениях нормированной корреляционной функции  и
и  .
.
На рисунках четко видно, что при положительной корреляции (ρ=0,8) с увеличением значения, принимаемого реализацией случайного сигнала в одном сечении, увеличивается ее значение и в соседнем сечении. При отрицательной корреляции эта тенденция изменяется на обратную зависимость. При отсутствии корреляции поверхность, описывающая двухмерную плотность распределения, становится осесимметричной и взаимосвязь между значениями реализаций сигнала в соседних сечениях исчезает.
Таким образом, корреляционная функция дает нам полное описание нормального случайного стационарного сигнала. Как мы сейчас увидим, характер затухания корреляционной функции теснейшим образом связан со спектром мощности сигнала.
4.3 Эргодические случайные сигналы
Случайный стационарный сигнал называется эргодическим, если каждая его реализация, достаточно протяженная по времени, несет в себе полную информацию о всем ансамбле реализаций. Дело обстоит таким образом, как будто эту длинную реализацию можно разрезать на несколько частей и их совокупность рассматривать как совокупность реализаций. В этом случае множество значений случайного сигнала в различные моменты времени идентично множеству значений, принимаемых множеством реализаций сигнала в одном сечении.
Свойство эргодичности позволяет получить все характеристики сигнала по одной единственной реализации и не рассматривать ансамбль реализаций. По одной реализации сигнала  длительностью Т можно вычислить:
длительностью Т можно вычислить:
- оценку математического ожидания сигнала
 ,
,
- оценку дисперсии сигнала
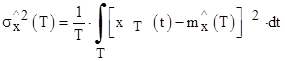
- автокорреляционную функцию сигнала
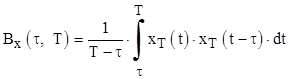
Последняя формула нуждается в некоторых комментариях. Если сигнал  сдвинуть по времени на величину τ, то окажется, что произведение сигнала на его сдвинутую копию существует только на интервале Т-τ, поэтому и пределы интегрирования выбраны соответствующим образом.
сдвинуть по времени на величину τ, то окажется, что произведение сигнала на его сдвинутую копию существует только на интервале Т-τ, поэтому и пределы интегрирования выбраны соответствующим образом.
Будем рассматривать только класс стационарных центрированных случайных сигналов, из состава которых удалено математическое ожидание как детерминированная составляющая сигнала. Тогда при достаточно больших Т для выполнения свойства эргодичности должно иметь место равенство  ,
,
то есть усреднение эргодического сигнала по времени равносильно его усреднению по времени.
Оценка дисперсии эргодического сигнала при больших Т должна приближаться к дисперсии сигнала, определенной по ранее введенным правилам
 .
.
Пределом автокорреляционной функции при больших Т должна стать корреляционная функция случайного эргодического стационарного сигнала
 .
.
Это последнее соотношение является наиболее важным, так как позволяет по одной единственной, хотя и достаточно длинной реализации определить корреляционную функцию сигнала, которая полностью характеризует все его свойства.
4.4 Спектральное представление случайных сигналов
При изучении непериодических сигналов мы пользовались их спектральное представление с помощью интеграла Фурье.
Спектральная функция для сигнала x(t) определялась при этом как комплексная функция частоты
 ,
,
которая характеризовала распределение амплитуд и фаз по частотам гармонических составляющих сигнала x(t).
При изучении случайных процессов так же желательно определять их спектр, но характеризующий не отдельную реализацию процесса, а весь ансамбль реализаций в целом. Однако при попытке использования аппарата преобразования Фурье к анализу случайных процессов возникает ряд трудностей.
1. Интеграл Фурье существует только для абсолютно интегрируемых сигналов или хотя бы для сигналов, интегрируемых в квадрате, т.е. функция x(t) должна быть такой, чтобы выполнялось условие
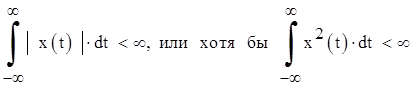
2. Однако последний интеграл представляет собой энергию реализации случайного сигнала. Таким образом, преобразование Фурье существует только для реализаций с конечной энергией. Однако стационарные эргодические центрированные процессы (с нулевым средним значением) имеют конечную мощность реализаций, равную дисперсии сигнала:
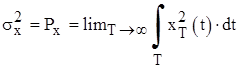
Они задаются на бесконечном интервале времени  , поэтому их энергия должна быть бесконечно велика. Следовательно, преобразования Фурье для них не существует.
, поэтому их энергия должна быть бесконечно велика. Следовательно, преобразования Фурье для них не существует.
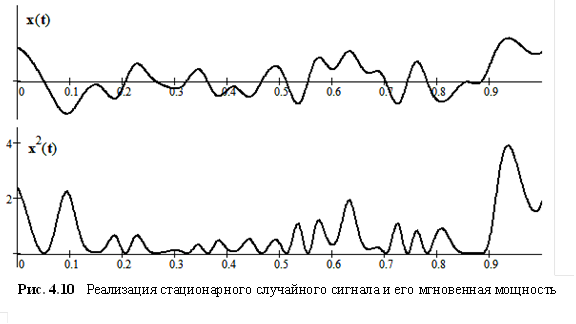 |
3. Реализации таких процессов имеют вид случайных колебаний вокруг среднего (рис. 4.10, верхний график). Площадь под кривой, описывающей квадрат сигнала (мгновенная мощность, нижний график на рис. 4.10), бесконечно велика. Поэтому бесконечно велика и энергия такого сигнала, равная сумме площадей под этими, всегда положительными импульсами.
4. Реализации с конечной энергией должны затухать во времени, то есть должны быть нестационарными. Для каждой такой реализации можно определить спектральную функцию. Однако такая функция почти бесполезна для анализа ансамбля реализаций, поскольку каждая такая реализация для нестационарного, а значит и неэргодического сигнала не является достаточно представительной для описания всего ансамбля.
Выход заключается в отбрасывании спектра фаз и построении функции, характеризующей распределение энергии реализации по ее гармоническим составляющим.
Вначале рассмотрим реализацию  сигнала X(t) с конечной энергией, для которой существует спектральная функция
сигнала X(t) с конечной энергией, для которой существует спектральная функция  . Для каждой реализации сигнала справедлива теорема Парсеваля:
. Для каждой реализации сигнала справедлива теорема Парсеваля:
 ,
,
где f = w/2p — частота в герцах.
Функция  характеризует, таким образом, распределение энергии данной реализации сигнала по оси частот, подобно тому, как спектральная функция
характеризует, таким образом, распределение энергии данной реализации сигнала по оси частот, подобно тому, как спектральная функция  характеризует распределение амплитуд по частотам гармонических составляющих сигнала. Назовем ее спектральной плотностью энергии реализации.
характеризует распределение амплитуд по частотам гармонических составляющих сигнала. Назовем ее спектральной плотностью энергии реализации.
После усреднения этой функции по всем реализациям данного процесса получаем спектральную плотность энергии процесса в целом:
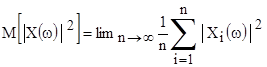
Рассмотрим некоторые свойства спектральной плотности энергии сигнала:
а) Данная функция является неотрицательной функцией частоты.
б) Площадь под кривой, отображающей эту функцию, равна математическому ожиданию энергии процесса.
в) Поскольку x(t) — действительная функция, то  — четная функция частоты. Поэтому о спектральном составе энергии сигнала можно судить лишь по одной половине графика, построенной, например, для положительных частот.
— четная функция частоты. Поэтому о спектральном составе энергии сигнала можно судить лишь по одной половине графика, построенной, например, для положительных частот.
При анализе стационарных эргодических центрированных сигналов X(t) возьмем одну достаточно длинную реализацию xT(t) протяженностью Т. Конечная реализация имеет и конечную энергию, поэтому для нее можно определить спектральную функцию X(ω).
Спектральная плотность энергии после усреднения по реализациям одной и той же длины Т имеет вид
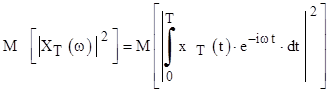
Разделив ее на длину реализации, получим спектральную плотность мощности
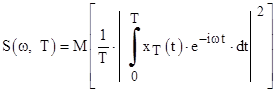
Предел этого отношения при T®¥ определяет спектральную плотность мощности стационарного центрированного случайного сигнала или его энергетический спектр:
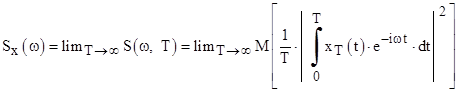
Энергетический спектр характеризует распределение мощности реализации сигнала или его дисперсии (что то же самое) по частотам отдельных гармонических составляющих. Энергетический спектр — это неотрицательная четная функция частоты, ограничивающая фигуру, площадь которой равна средней мощности, то есть дисперсии сигнала
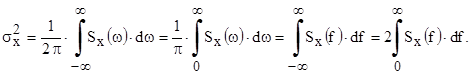


 Часто используются модели случайных сигналов, в которых спектр отличен от нуля только в некоторой ограниченной полосе частот w1 < w < w2 или f1 < f < f2. Такие сигналы называются сигналами с финитным спектром. Разность частот F = f2 – f1 или W = w2 - w1 называется шириной спектра. В реальных условиях спектр жестко не ограничен по протяженности. Тогда под шириной спектра понимают ширину той минимальной полосы частот, в которой сосредоточена подавляющая часть (например, 95%) всей мощности сигнала (рис. 4.11).
Часто используются модели случайных сигналов, в которых спектр отличен от нуля только в некоторой ограниченной полосе частот w1 < w < w2 или f1 < f < f2. Такие сигналы называются сигналами с финитным спектром. Разность частот F = f2 – f1 или W = w2 - w1 называется шириной спектра. В реальных условиях спектр жестко не ограничен по протяженности. Тогда под шириной спектра понимают ширину той минимальной полосы частот, в которой сосредоточена подавляющая часть (например, 95%) всей мощности сигнала (рис. 4.11).
4.5 Теорема Винера - Хинчина
Американским ученым Н. Винером и русским математиком А.Я. Хинчиным одновременно и независимо друг от друга было найдено интересное соотношение между корреляционной функцией стационарного эргодического центрированного случайного процесса и его энергетическим спектром. Спектральная плотность мощности (энергетический спектр или спектр дисперсий) стационарного центрированного случайного эргодического сигнала его корреляционная функция связаны друг с другом преобразованием Фурье:
 .
.
Заменим комплексные экспоненты в этих выражениях по формулам Эйлера через тригонометрические функции. Поскольку функция  являются четными, то и интегралы от произведений
являются четными, то и интегралы от произведений  и
и  в бесконечных пределах обращаются в нуль. Произведения
в бесконечных пределах обращаются в нуль. Произведения  и
и  — функции четные.
— функции четные.
Поэтому интегрирование можно провести только для положительных значений аргументов, а результаты удвоить. В результате получаются более комфортные выражения для связи между корреляционной функцией и спектральной плотность мощности стационарного центрированного случайного эргодического сигнала:
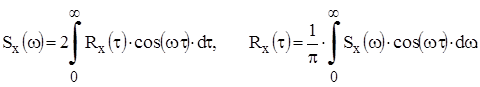
Пример.
 Сигнал со спектральной плотностью мощности, постоянной вплоть до некоторой граничной частоты
Сигнал со спектральной плотностью мощности, постоянной вплоть до некоторой граничной частоты  , называется низкочастотным белым шумом (рис. 4.12). Его спектральная мощность:
, называется низкочастотным белым шумом (рис. 4.12). Его спектральная мощность:
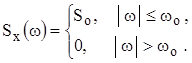
Бесплатная лекция: "15 Системные описания" также доступна.
Графики спектральной плотности мощности двух сигналов с граничными частотами  представлены на рис. 4.12. Оба сигнала имеют одинаковую мощность, равную 190 м
представлены на рис. 4.12. Оба сигнала имеют одинаковую мощность, равную 190 м и определяемую как площадь фигуры, образованной графиком спектральной плотности и осью абсцисс, деленной на π=3,141593.
и определяемую как площадь фигуры, образованной графиком спектральной плотности и осью абсцисс, деленной на π=3,141593.
Согласно теореме Винера – Хинчина, корреляционная функция низкочастотного белого шума должна выглядеть следующим образом:
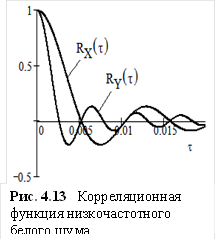
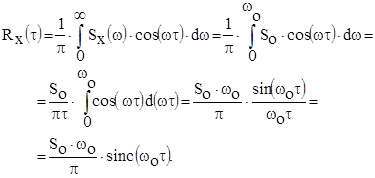
Графики корреляционной функции этих двух сигналов представлены на рис. 4.13. Чем шире частотный спектр сигнала, тем более круто затухает корреляционная функция. В сечениях сигнала, разделенных интервалами времени
 ,
,
 значения реализаций сигнала не коррелированны, то есть, не зависимы друг от друга. По мере расширения частотного диапазона сигнала эти сечения располагаются все чаще и, в конце концов, корреляционная функция превращается в δ – импульс в начале координат.
значения реализаций сигнала не коррелированны, то есть, не зависимы друг от друга. По мере расширения частотного диапазона сигнала эти сечения располагаются все чаще и, в конце концов, корреляционная функция превращается в δ – импульс в начале координат.





















