Помехоустойчивое кодирование, кодеки дискретного канала

ГЛАВА 10. Помехоустойчивое кодирование, кодеки дискретного канала

10.1. Принципы построения корректирующих кодов

         Повышение требований к скорости и достоверности передачи информации, увеличение протяженности линий связи приводит к необходимости применения специальных мер, уменьшающих вероятность появления ошибок. В настоящее время найден ряд возможностей для решения указанной задачи. Одной из них является применение помехоустойчивого кодирования.

         Под помехоустойчивыми понимаются коды, позволяющие обнаруживать и исправлять ошибки, возникающие при передаче из-за действия помех. Идея их построения заключается в том, что из N₀ возможных комбинаций длиной n применяется лишь некоторая часть. Пусть их число равно N. Используемые при передаче кодовые комбинации обычно называются разрешенными, а остальные, число которых N₀-N, - запрещенными.

         Поясним способность кода исправлять ошибки. Разобьем множество кодовых комбинаций на N подмножеств M_i, i=1,2,…,N, и каждому подмножеству поставим в соответствие разрешенную кодовую комбинацию B_i. Зададимся следующим правилом приема: если принятая кодовая комбинация попадает в подмножество M_i, то принимается решение в пользу кодовой комбинации B_i. Очевидно, что при таком правиле приема будут исправляться все те ошибки, которые не выводят передаваемую кодовую комбинацию за пределы принадлежащего ей подмножества.

         При построении кода, работающего в режиме декодирования с исправлением ошибок, основной сложностью является разбиение множества запрещенных кодовых комбинаций на N подмножеств и сопоставление их разрешенным кодовым комбинациям. Очевидно, что для уменьшения вероятности ошибочного декодирования в подмножество M_i следует включать те запрещенные кодовые комбинации  , для которых

где P(B_i) - априорная вероятность передачи кодовой комбинации B_i,  - условная вероятность принятия кодовой комбинации  при передаче кодовой комбинации B_i. Таким образом, в подмножество M_i должны входить кодовые комбинации , при приеме которых наиболее вероятной переданной комбинацией является B_i.

         При декодировании по максимуму правдоподобия решение принимается в пользу кодовой комбинации B_i, если вероятность  максимальна. Для симметричного двоичного канала без памяти

Рекомендуемые материалы

              (10.1)

Где р_ош - вероятность искажения символа,  - число разрядов, в которых комбинации  и B_i отличаются друг от друга (расстояние Хэмминга между B_k и B_i). Из (10.1) следует, что при р_ош<1/2 вероятность  монотонно убывает с возрастанием расстояния , принимая максимальное значение для кодовой комбинации B_i, которая отличается от принятой комбинации  в меньшем числе символов. Таким образом, сформулированное правило декодирования соответствует критерию максимума правдоподобия.

10.2. Классификация кодов

Известно большое число помехоустойчивых кодов, которые классифицируются по различным признакам. Прежде всего помехоустойчивые коды можно разделить на два больших класса: блочные и непрерывные. При блочном кодировании последовательность элементарных сообщений источника разбивается на отрезки и каждому отрезку ставится в соответствие определенная последовательность (блок) кодовых символов, называемая обычно кодовой комбинацией. Множество всех кодовых комбинаций, возможных при данном способе блочного кодирования, и есть блочный код.

         Длина блока может быть как постоянной, так и переменной. Соответственно различают равномерные и неравномерные блочные коды. Помехоустойчивые коды являются, как правило, равномерными. Поэтому неравномерные коды в дальнейшем не рассматриваются.

         Блочные коды бывают разделимыми и неразделимыми. К разделимым относятся коды, в которых символы по их назначению могут быть разделены на информационные (символы, несущие информацию о сообщениях) и проверочные. Такие коды обозначаются как (n, k), где n - длина кода, k - число информационных символов. Число комбинаций в коде не превышает 2^k. К неразделимым относятся коды, символы которых нельзя разделить по их назначению на информационные и проверочные. К ним относятся, например, коды с постоянным весом и коды на основе матриц Адамара.

         Среди разделимых кодов различают линейные и нелинейные. К линейным относятся коды, в которых поразрядная сумма по модулю 2 любых двух кодовых слов также является кодовым словом. Линейный код называется систематическим, если первые k символов его любой кодовой комбинации являются информационными, остальные (n-k) символов - проверочными.

         Среди линейных систематических кодов наиболее простым является код (n, n-k), содержащий один проверочный символ, который равен сумме по модулю 2 всех информационных символов. Этот код, называемый кодом с проверкой на четность, позволяет обнаружить все сочетания ошибок нечетной кратности. Вероятность необнаруженной ошибки в первом приближении можно определить как вероятность искажения двух символов:

         Подклассом линейных кодов являются циклические коды. Они характеризуются тем, что все наборы, образованные циклической перестановкой любой кодовой комбинации, являются также кодовыми комбинациями. Это свойство позволяет в значительной степени упростить кодирующее и декодирующее устройства, особенно при обнаружении ошибок и исправлении одиночной ошибки. Примерами циклических кодов являются коды Хэмминга, коды Боуза - Чоудхури - Хоквингема (БЧХ - коды) и др.

         Непрерывные коды характеризуются тем, что операции кодирования и декодирования производятся над непрерывной последовательностью символов без разбиения ее на блоки. Среди непрерывных наиболее применимы сверточные коды.

10.3. Основные характеристики и корректирующие свойства

 блочных кодов

К числу основных характеристик кода относятся длина кода n, его основание m, мощность N (число разрешенных кодовых комбинаций), полное число кодовых комбинаций N₀, число информационных символов k, число проверочных символов r = n - k, вес кодовой комбинации (число единиц в комбинации), избыточность кода, кодовое расстояние. Из перечисленных характеристик лишь две последние нуждаются в пояснении.

         Избыточность кода в общем случае определяется выражением

или для двоичного кода (m=2) при N=2^k

где величина k/n называется относительной скоростью кода.

         Введем понятие кодового расстояния. Предварительно отметим, что для оценки отличия одной кодовой комбинации от другой можно использовать расстояние Хэмминга d(B_i, B_j), определяемое числом разрядов, в которых одна кодовая комбинация отличается от другой. Для двоичного кода

где b_ik и b_jk -  символы кодовых комбинаций B_i и B_j соответственно, ⊕ - символ суммирования по модулю 2. Наименьшее расстояние Хэмминга для данного кода называется кодовым расстоянием. В дальнейшем его будем обозначать через d.

         Если существует блочный линейный код (n, k), то для него справедливо неравенство

                                      (10.2)

называемое верхней границей Хэмминга, где  означает целую часть числа  .

         Граница Хэмминга (10.2) близка к оптимальной для кодов с большими значениями k/n. Для кодов с малыми значениями k/n более точной является верхняя граница Плоткина:

                               (10.3)

         Можно также показать, что существует блочный линейный код (n, k) с кодовым расстоянием d, для которого справедливо неравенство

                                (10.4)

называемое нижней границей Варшамова - Гильберта.

         Таким образом, границы Хэмминга и Плоткина являются необходимыми условиями существования кода, а граница Варшамова - Гильберта - достаточным.

         Приведенные границы (10.2), (10.3) и (10.4) можно обобщить на недвоичные коды, а границу (10.3) - и на нелинейные.

         Равенство в (10.2) справедливо только для так называемых совершенных кодов. Они исправляют все ошибки кратности [(d-1)/2] и не менее и не исправляют ни одной ошибки кратности  где  - целая часть числа . Следует отметить, что число совершенных кодов невелико. Примером таких кодов являются коды Хэмминга.

         Равенство в (10.3) справедливо только для эквидистантных кодов, в которых расстояние Хэмминга между любыми двумя различными кодовыми комбинациями одно и то же. К ним относятся, например, коды, построенные на основе матриц Адамара.

10.4. Блочные коды. Построение кодеков

10.4.1. Линейные коды

         Из определения следует, что любой линейный код (n, k) можно получить из k  линейно независимых кодовых комбинаций путем их посимвольного суммирования по модулю 2 в различных сочетаниях. Исходные линейно - независимые кодовые комбинации называются базисными.

         Представим базисные кодовые комбинации в виде матрицы

                                (10.5)

         В теории кодирования она называется порождающей. Тогда процесс кодирования заключается в выполнении операции B=AG, где А - вектор размерностью k, соответствующий сообщению, B - вектор размерностью n, соответствующий кодовой комбинации.

         Таким образом, порождающая матрица (10.5) содержит всю необходимую для кодирования информацию. Она должна храниться в памяти кодирующего устройства. Для двоичного кода объем памяти равен двоичных символов. При табличном задании кодирующее устройство должно запомнить  двоичных символов.

         Две порождающие матрицы, которые отличаются друг от друга только порядком расположения столбцов, задают коды, которые имеют одинаковое расстояние Хэмминга между соответствующими кодовыми комбинациями, а следовательно, одинаковые корректирующие способности. Такие коды называются эквивалентными.

         Линейный (n, k) код может быть задан так называемой проверочной матрицей Н размерности . При этом комбинация В принадлежит коду только в том случае, если вектор В ортогонален всем строкам матрицы Н, т.е. если выполняется равенство

                                         (10.6)

где Т - символ транспонирования матрицы.

         Так как (10.6) справедливо для любой кодовой комбинации, то

         Каноническая форма матрицы Н имеет вид

         (10.7)

где Р^Т - подматрица, столбцами которой служат строки подматрицы Р (10.5),   I - единичная  подматрица.

         Подставляя (10.7) в (10.6), можно получить n-k уравнений вида

                 (10.8)

которые называются уравнениями проверки.

         С помощью проверочной матрицы сравнительно легко можно построить с заданным кодовым расстоянием. Это построение основано на следующей теореме: кодовое расстояние линейного (n, k) кода равно d тогда и только тогда, когда любые d-1 столбцов проверочной матрицы этого кода линейно независимы, но некоторые d столбцов проверочной матрицы линейно зависимы.      Заметим, что строки проверочной матрицы линейно независимые. Поэтому проверочную матрицу можно использовать в качестве порождающей для некоторого другого линейного кода (n, n-k), называемого двойственным.

         Кодирующее устройство для линейного кода (n, k) (рис. 10.1) состоит из k- разрядного сдвигающего регистра и r = n - k блоков сумматоров по модулю 2. Информационные символы одновременно поступают на вход регистра и на выход кодирующего устройства через коммутатор К. С поступлением k-го информационного символа на выходах блоков сумматоров в соответствии с уравнениями (10.8) формируются проверочные символы, которые затем поступают на выход кодера.

         Процесс декодирования сводится к выполнению операции

где S - вектор размерностью (n-k), называемый синдромом,  - вектор принятой кодовой комбинации.

         Если принятая кодовая комбинация  совпадает с одной из разрешенных В (это имеет место тогда, когда - либо ошибки в принятых символах отсутствуют, либо из-за действия помех одна разрешенная комбинация переходит в другую), то

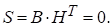
В противном случае , причем вид синдрома зависит только от вектора ошибок е. Действительно

где В - вектор, соответствующий передаваемой кодовой комбинации. При S=0 декодер принимает решение об отсутствии ошибок, а при  - о наличии ошибок. Число различных синдромов, соответствующих различным сочетаниям ошибок, равно 2^n-k-1. По конкретному виду синдрома можно в пределах корректирующей способности кода указать на ошибочные символы и их исправить.

         Декодер линейного кода (рис. 10.2) состоит из k-разрядного сдвигающего регистра, n-k блоков сумматоров по модулю 2, схемы сравнения, анализатора ошибок и корректора. Регистр служит для запоминания информационных символов принятой кодовой последовательности, из которых в блоках сумматоров формируются проверочные символы. Анализатор ошибок по конкретному виду синдрома, получаемого в результате сравнения формируемых на приемной стороне и принятых проверочных символов, определяет места ошибочных символов. Исправление информационных символов производится в корректоре.

Заметим, что в общем случае при декодировании линейного кода с исправлением ошибок в памяти декодера должна храниться таблица соответствий между синдромами и векторами ошибок, содержащая 2^n-k строк. С приходом каждой кодовой комбинации декодер должен перебрать всю таблицу. При небольших значениях n-k эта операция не вызывает затруднений. Однако для высокоэффективных кодов длиной n, равной нескольким десяткам, разность n-k принимает такие значения, что перебор таблицы из 2^n-k строк оказывается практически невозможным. Например, для кода, имеющего кодовое расстояние d = 5, таблица состоит из 2¹² = 4096 строк.

При заданных значениях n и k существует 2^k(n-k) линейных кодов. Задача заключается в выборе наилучшего (с позиции того или иного критерия) кода.

10.4.2. Циклические коды

Циклические коды относятся к классу линейных систематических. Поэтому для их построения в принципе достаточно знать порождающую матрицу.

Можно указать другой способ построения циклических кодов, основанный на представлении кодовых комбинаций многочленами b(x) вида

где b_n-1 b_n-2 … b₀ -кодовая комбинация. Над данными многочленами можно производить все алгебраические действия с учетом того, что сложение здесь осуществляется по модулю 2.

         Каждый циклический код (n, k) характеризуется так называемым порождающим многочленом. Им может быть любой многочлен р(х) степени n-k, который делит без остатка двучлен . Циклические коды характеризуются тем, что многочлены b(х) кодовых комбинаций делятся без остатка на р(х). Поэтому процесс кодирования сводится к отысканию многочлена b(х) по известным многочленам а(х) и р(х), делящегося на р(х), где а(х) - многочлен степени k-1, соответствующий информационной последовательности символов.

         Очевидно, что в качестве многочлена b(х) можно использовать произведение а(х)р(х). Однако при этом информационные и проверочные символы оказываются перемешанными, что затрудняет процесс декодирования. Поэтому на практике в основном применяется следующий метод нахождения многочлена b(x).

         Умножим многочлен а(х) на х^n-k и полученное произведение разделим на р(х). Пусть

                            (10.9)

где m(х) - частное, а с(х) - остаток. Так как операции суммирования и вычитания по модулю 2 совпадают, то выражение (10.9) перепишем в виде

                          (10.10)

Из (10.10) следует, что многочлен  делится на р(х) и, следовательно, является искомым.

         Многочлен a(x)x^n-k имеет следующую структуру: первые n-k членов низшего порядка равны нулю, а коэффициенты остальных совпадают с соответствующими коэффициентами информационного многочлена а(х). Многочлен с(х) имеет степень меньше n-k. Таким образом, в найденном многочлене b(x) коэффициенты при х в степени n-k и выше совпадают с информационными символами, а коэффициенты при остальных членах, определяемых многочленом с(х), совпадают с проверочными символами.

         В соответствии с (10.10) процесс кодирования заключается в умножении многочлена а(х) на x^n-k и нахождении остатка от деления

а(х)х^n-k на р(х) с последующим его сложением по модулю 2 с многочленом

а(х)х^n-k.

         На рис. 10.3. в качестве примера приведена схема кодера для кода (7, 4) с порождающим многочленом . В исходном состоянии ключи К1 и К2 находятся в положении 1. Информационные символы поступают одновременно на вход канала и на выход ячейки х³ сдвигающего регистра (это соответствует умножению многочлена а(х) на х³). В течение четырех тактов происходит деление многочлена а(х)х³ на многочлен . В результате в регистре записывается остаток, представляющий собой проверочные символы. Ключи К1 и К2 перебрасываются в положение 2, и в течение трех последующих тактов содержащиеся в регистре символы поступают в канал.

         Циклический код может быть задан проверочным многочленом h(x): кодовая комбинация В принадлежит данному циклическому коду, если . Проверочный многочлен связан с порождающим отношением

         Задание кода проверочным многочленом эквивалентно заданию кода системой проверочных уравнений (10.8). Характерной особенностью циклического кода является то, что все проверочные уравнения можно получить из одного путем циклического сдвига индексов символов, входящих в исходное уравнение. Так, для кода (7, 4) с порождающим многочленом  проверочный многочлен имеет вид . Проверочные уравнения получаются из условия

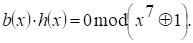
         Осуществив умножение и приравняв коэффициенты при х⁴, х⁵ и х⁶ нулю, получим следующие уравнения

                                      (10.11)

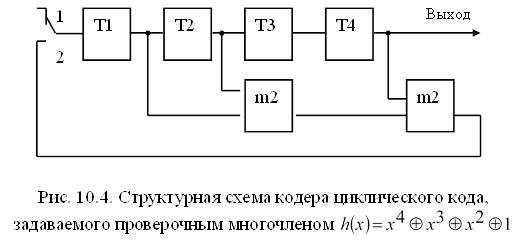
В качестве примера на рис.10.4 показана схема кодера циклического кода (7, 4), задаваемого проверочным многочленом  или, что то же самое, проверочными соотношениями (10.11). в исходном состоянии ключ находится в положении 1. В течение четырех тактов импульсы поступают в регистр, после чего ключ переводится в положение 2. При этом обратная связь замыкается. Начиная с пятого такта, формируются проверочные символы в соответствии с (10.11). После седьмого такта все проверочные символы оказываются сформированными, ключ вновь переключается в положение 1. Кодер готов к приему очередного сообщения. Символы кодовой комбинации поступают в канал, начиная с пятого такта.

         Корректирующая способность кода зависит от порождающего многочлена р(х). Поэтому его выбор очень важен при построении циклического кода. Необходимо помнить, что степень порождающего многочлена должна быть равна числу проверочных символов. Кроме того, многочлен р(х) должен делить двучлен .

         Обнаружение ошибок при использовании таких кодов заключается в делении многочлена , соответствующего принятой комбинации , на р(х). Если остаток s(х) оказывается равным нулю, то считается, что ошибки нет, в противном случае фиксируется ошибка.

         Один из алгоритмов исправления ошибок основан на следующих свойствах циклического кода. Пусть имеется циклический код с кодовым расстоянием d, исправляющий все ошибки до кратности  включительно, где   - целая часть числа . Тогда можно показать, что

¨ если исправляемый вектор ошибок искажает только проверочные символы, то вес синдрома будет меньше или равен , а сам синдром будет совпадать с вектором ошибок;

¨ если вектор ошибки искажает хотя бы один информационный символ, то вес синдрома будет больше ;

¨ если s(х) - остаток от деления многочлена b(х) на р(х), то остатком от деления многочлена b(x)xⁱ на р(х) является многочлен s(x)xⁱmodp(x), другими словами, синдром некоторого циклического сдвига многочлена b(х) является соответствующим циклическим сдвигом синдрома исходного многочлена, взятого по модулю р(х).

         Существуют и другие, более универсальные алгоритмы декодирования.

         К циклическим кодам относятся коды Хэмминга, которые являются примерами немногих известных совершенных кодов. Они имеют кодовое расстояние d=3 и исправляют все одиночные ошибки. Длина кода выбирается из условия 2^n-k-1 = n, которое имеет простой смысл: число различных ненулевых синдромов равно числу символов в кодовой последовательности. Так существуют коды Хэмминга (2^r-1, 2^r-r-1), в частности коды (7,4), (15,11), (31,26), (63,57) и т.д.

         Заметим, что ранее использованный многочлен  является порождающим для кода Хэмминга (7,4).

         Среди циклических кодов широкое применение нашли коды Боуза-Чоудхури-Хоквингема (БЧХ). Можно показать, что для любых целых положительных чисел m и  существует двоичный код БЧХ длины        n = 2^m-1 с кодовым расстоянием , причем число проверочных символов .

         Для кодов БЧХ умеренной длины и ФМ при передаче символов можно добиться значительного выигрыша (4 дБ и более). Он достигается при скоростях . При очень высоких и очень низких скоростях выигрыш от кодирования существенно уменьшается.

10.4.3. Мажоритарные циклические коды

         Иногда целесообразно использовать коды с несколько худшей корректирующей способностью по сравнению с лучшими известными кодами, но простые в реализации. К ним относятся коды, допускающие мажоритарное декодирование. Оно основано на возможности для некоторых циклических кодов выразить каждый информационный символ с помощью Q различных линейных соотношений. Решение о значении символа принимается по большинству значений, даваемых каждым отдельным соотношением. Для исправления всех ошибок до кратности  включительно необходимо иметь  независимых соотношений.

         В некоторой области значений параметров мажоритарные коды имеют корректирующую способность незначительно уступающую корректирующей способности кодов БЧХ. В то же время их реализация сравнительно проста.

         Проиллюстрируем принцип мажоритарного декодирования на примере кода (7.3) с проверочной матрицей

                    (10.12)

         Рассматриваемый код является циклическим с порождающим многочленом . Он имеет кодовое расстояние d = 4.

         Используя матрицу (10.12), можно записать следующие соотношения для символа b₁:

                   (10.13)

         С учетом (10.13) в декодере имеется возможность четырьмя разными способами вычислить первый информационный символ:

                      (10.14)

где  - принятая кодовая комбинация.

         При отсутствии ошибок , т.е. все проверочные соотношения (10.14) дают один и тот же результат. При наличии одного ошибочного символа три проверочных соотношения дают правильное значение, а соотношение, в котором участвует ошибочный символ, дает неверный результат. Принимая решение по большинству, декодер выдает правильный символ b₁.

         Пусть ошибочно приняты два символа. Если они входят в различные проверочные соотношения, то две проверки дадут значение 1, а две проверки - значение 0. В этом случае декодер выдает сигнал отказа от декодирования. Если оба искаженных символа входят в одно проверочное соотношение, то все четыре проверки выдают один и тот же результат. Декодер выдает правильный символ b₁.

         Аналогично определяются остальные информационные символы. Проверочные соотношения для символов  и  получаются из (10.14) циклической перестановкой:

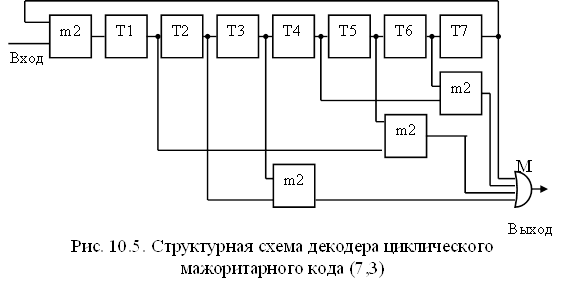
         Схема декодера (рис.10.5) состоит из сдвигающего регистра, сумматоров по модулю 2 и мажоритарного элемента М. Простота ее обусловлена тем, что в данном случае каждый символ кодовой комбинации участвует в одном проверочном соотношении. Код, для которого выполняется это условие, называется кодом с разделенными проверками.

         Мажоритарное декодирование возможно и тогда, когда один и тот же символ участвует в нескольких проверочных соотношениях. Однако алгоритм декодирования усложняется.

10.5. Свёрточные коды

10.5.1. Методы задания сверточных кодов

         Сверточный код - это линейный рекуррентный код. В общем случае он образуется следующим образом. В каждый i-й тактовый момент времени на вход корректирующего устройства поступает k₀ символ сообщения: a_i1a_i2…a_ik0. Выходные символы b_i1b_i2…b_in0 формируются с помощью рекуррентного соотношения из К символов сообщения, поступивших в данный и в предшествующие тактовые моменты времени:

              (10.15)

где  - коэффициенты, принимающие значения 0 или 1.

         Символы сообщения, из которых формируются выходные символы, хранятся в памяти кодирующего устройства. Величина К называется длиной кодового ограничения. Она показывает, на какое максимальное число выходных символов влияет данный информационный символ, и играет ту же роль, что и длина блочного кода. Сверточный код имеет избыточность  и обозначается как ().

Типичные параметры сверточного кода: k₀, n₀ = 1, 2,…, 8; k₀/n₀ = 1/4…7/8; K = 3…10.

         Сверточный код получается систематическим, если в каждый тактовый момент k₀ выходных символов совпадают с символами сообщения. На практике обычно используются несистематические сверточные коды.

         Различают прозрачные и непрозрачные сверточные коды. Первые характеризуются свойством инвариантности по отношению к операции инвертирования кода, которое заключается в следующем: если значения символов на входе кодера поменять на противоположные, то выходная последовательность символов также инвертируется. Соответственно декодированная последовательность символов будет иметь такую же неопределенность в знаке, что и принятая последовательность символов, а следовательно, неопределенность знака последовательности можно устранить после декодирования сверточного кода. Указанное свойство прозрачных кодов особенно важно для СПИ, использующих противоположные фазоманипулированные сигналы, которым свойственно явление обратной работы.

         Для непрозрачного кода неопределенность знака последовательности символов приходится устранять до сверточного декодирования, что приводит к увеличению вероятности ошибок. Нетрудно показать, что сверточный код будет прозрачным, если каждый его порождающий многочлен содержит нечетное число членов.

         Помимо рассмотренного способа задания сверточного кода, возможны и другие. В частности, выходные символы можно рассматривать как свертку импульсной характеристики кодера с информационной последовательностью (отсюда происходит название кода).

10.5.2. Методы декодирования сверточных кодов

         Сверточные коды можно декодировать различными методами. Различают декодирование с вычислением и без вычисления проверочной последовательности.

         Декодирование с вычислением проверочной последовательности применяется только для систематических кодов. По своей сущности оно ничем не отличается от соответствующего метода декодирования блочных кодов. На приемной стороне из принятых информационных символов формируют проверочные символы по тому закону, что и на передающей стороне, которые затем сравнивают с принимаемыми проверочными символами. В результате сравнения формируется проверочная последовательность, которая при отсутствии ошибок состоит из одних нулей. При наличии ошибок на определенных позициях последовательности появляются единичные символы. Закон формирования проверочных символов выбирается таким образом, чтобы по структуре проверочной последовательности можно было определить искаженные символы.

         К числу методов декодирования без вычисления проверочной последовательности относятся декодирование по принципу максимума правдоподобия и последовательное декодирование.

         Декодирование по принципу максимума правдоподобия сводится к задаче отождествления принятой последовательности с одной из 2^N возможных, где N - длина информационной последовательности. Решение принимается в пользу той кодовой последовательности, которая в меньшем числе позиций отличается от принятой. Метод применим для любого сверточного кода. Однако при больших значениях N, он практически нереализуем из-за необходимости перебора 2^N возможных кодовых последовательностей. Существенное упрощение процедуры декодирования по максимуму правдоподобия предложил Витерби. Характерной особенностью его метода является то, что на каждом шаге декодирования запоминается только 2^К-1 наиболее правдоподобных путей.

         Алгоритм Витерби обладает рядом преимуществ. При небольших значениях длины кодового ограничения декодирующее устройство оказывается достаточно простым, реализуя в то же время высокую помехоустойчивость. Так, исследования показывают, что применение сверточных кодов с К = 3, 5 и 7 при фиксированной вероятности ошибки р_ош=10^-5 позволяет получить энергетический выигрыш 4…6 дБ по сравнению с системой, использующей ФМ сигналы без кодирования. Важным преимуществом по сравнению с методом последовательного декодирования является фиксация числа вычислительных операций на один декодированный символ. Декодирование по методу Витерби особенно перспективно в каналах с независимыми ошибками.

10.5.3. Реализация алгоритма Витерби

         Декодер Витерби (рис.10.6) состоит из синхронизатора, устройства управления и тактирования, устройства для вычисления метрики ветвей, устройства для обновления и хранения метрик ветвей, устройства для обновления и хранения гипотетических информационных последовательностей и решающего устройства.

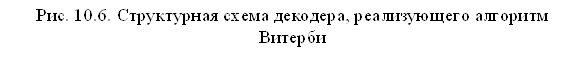Устройство хранения и обновления метрик путей осуществляет сложение метрик ветвей с хранящимися метриками путей, проделывает необходимые сравнение и запоминает новые метрики путей.

         Устройство хранения и обновления гипотетических информационных последовательностей может быть выполнено на сдвигающих регистрах, в каждом из которых хранится полная информационная последовательность символов, соответствующая одному из "выживших" путей. Их число равно числу узлов. После обработки новой ветви регистры обмениваются содержимым в соответствии с тем, какие последовательности "выживают" при сравнении. В последнюю ячейку каждого регистра поступает новый информационный символ, а самый старый символ каждого регистра поступает в выходное решающее устройство.

         Выходное решающее устройство принимает решение о переданных информационных символах. Наилучшие результаты получаются, когда в качестве переданного информационного символа берется наиболее старый символ в последовательности с наименьшей метрикой. Иногда используют мажоритарный принцип: за переданный информационный символ выбирается чаще всего встречающийся символ из самых старых символов всех последовательностей.

         Устройство управления и тактирования задает необходимый ритм работы декодера.

10.6. Использование кодов в системах с обратной связью

         Во многих системах кроме основного (прямого) канала, с помощью которого сообщение передается от источника кпотребителю, имеется обратный канал для вспомогательных сообщений, которые позволяют улучшить качество передачи сообщений по прямому каналу.

         Наиболее распространены системы с обратной связью, в которых для обнаружения ошибок применяют избыточные коды. Такие системы называются системами с решающей обратной связью, или системами с переспросом. В качестве кодов часто используют коды с проверкой на четность, простейшие интерактивные коды, циклические коды и др. Они позволяют хорошо обнаруживать ошибки при сравнительно небольшой избыточности и простой аппаратурной реализации.

         Передаваемое сообщение кодируется избыточным кодом. Полученная комбинация передается потребителю и одновременно запоминается в накопителе-повторителе. Принятая последовательность символов декодируется с обнаружением ошибок. Если при этом ошибки не обнаружены, то сообщение поступает потребителю. В противном случае сообщение бракуется и по обратному каналу передается специальный сигнал переспроса. По этому сигналу производится повторная передача забракованной кодовой комбинации, которая извлекается из накопителя-повторителя.

         Можно показать, что если в обратом канале ошибки отсутствуют, то остаточная вероятность ошибочного приема кодовой комбинации

,

где Р_н.о - вероятность необнаруженной ошибки (вероятность того, что переданная кодовая комбинация перешла в другую разрешенную), Р_о.о - вероятность обнаружения ошибки (вероятность того, что вместо переданной кодовой комбинации принята какая-либо запрещенная кодовая комбинация). Вероятности  и  можно найти, если известны свойства канала и задан код.

         Соответственно эквивалентная вероятность ошибки определяется как

,

где k - число информационных символов в кодовой комбинации.

         Среднее число передач одного сообщения

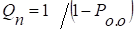
         Хотя обратный канал можно сделать весьма помехоустойчивым (обычно скорость передачи информации в обратном канале значительно меньше, чем в прямом), тем не менее существует конечная вероятность того, что сигнал переспроса будет принят как сигнал подтверждения, и наоборот. В первом случае сообщение не поступает к потребителю, а во втором случае оно поступает дважды.

         Одним из средств борьбы с ошибками в обратном канале, приводящими к потере сообщения, является использование несимметричного правила декодирования, при котором вероятность ошибки приема сигнала переспроса существенно меньше вероятности ошибочного приема сигнала подтверждения. Например, сигнал переспроса передается кодовой комбинацией из n единичных символов, а сигнал подтверждения - комбинацией из n нулей. При приеме кодовой комбинации, содержащей хотя бы одну единицу, решение принимается в пользу сигнала переспроса. Очевидно, что в этом вероятность ошибочного приема сигнала переспроса может быть сделана ничтожно малой.

         Для того чтобы к потребителю не поступали лишние сообщения из-за ошибочного приема сигнала подтверждения, передаваемые кодовые комбинации либо снабжаются номерами, либо дополняются опознавательными символами, по которым можно узнать, передается ли кодовая комбинация в первый раз или она повторяется. При этом принятая повторная комбинация при отсутствии сигнала переспроса стирается и не поступает потребителю. Возможны и другие способы борьбы с такого рода ошибками.

         Системы с решающей обратной связью весьма эффективны в случае каналов с замираниями. При ухудшении состояния канала увеличивается частота переспроса (уменьшается скорость передачи информации), но вероятность ошибочных сообщений, поступающих потребителю, практически не увеличивается. При улучшении состояния канала частота переспроса уменьшается. Таким образом, система как бы автоматически приспосабливается к состоянию канала связи, используя все его возможности в отношении передачи информации.

         Следует заметить, что применение решающей обратной связи, конечно, не увеличивает пропускной способности прямого канала, но позволяет простыми средствами по сравнению с длинными кодами приблизить скорость передачи информации к пропускной способности канала.

10.7. Сигнально-кодовые комбинации

         Как известно, многопозиционные сигналы, такие, как сигналы многократной ФМ, сигналы АФМ, обеспечивают высокую удельную скорость передачи информации (высокую частотную эффективность) при уменьшении энергетической эффективности, а помехоустойчивые коды позволяют повышать энергетическую эффективность при снижении удельной скорости передачи. Сочетание методов многопозиционной модуляции и помехоустойчивого кодирования дает возможность повысить либо энергетическую эффективность без уменьшения частотной, либо частотную эффективность без уменьшения энергетической, а в ряде случаев - оба параметра. Задача заключается в формировании сигнальных последовательностей, которые можно достаточно плотно разместить в многомерном пространстве (для обеспечения высокой частотной эффективности) и в то же время разнести на достаточно большие расстояния (для обеспечения высокой энергетической эффективности). Такие последовательности, построенные на базе помехоустойчивых кодов и многопозиционных сигналов с плотной упаковкой, называют сигнально-кодовыми конструкциями.

         В качестве помехоустойчивого кода обычно используют каскадные, интерактивные и сверточные коды, а в качестве многопозиционных сигналов - сигналы многократной ФМ и сигналы АФМ.

         Для согласования кодека двоичного помехоустойчивого кода и модема многопозиционных сигналов используется манипуляционный код, при котором большему расстоянию по Хэммингу между кодовыми комбинациями соответствует большее расстояние между соответствующими им сигналами. Этому требованию частично удовлетворяет код Грея. Возможны и другие способы такого преобразования.

10.8. Прием кодированных сигналов в целом

         До сих пор предполагалось, что кодовые комбинации принимаются посимвольно, т.е. на приемной стороне вначале выносится решение о каждом символе кодовой комбинации, а затем по совокупности n принятых символов принимается решение о том, какая кодовая комбинация была передана.

         При избыточных кодах такая двухэтапная процедура принятия решения оказывается неоптимальной. Объясняется это тем, что процесс демодуляции является необратимой операцией и может сопровождаться потерей информации. Действительно, после принятия решения о символе ни соответствующий элемент сигнала, ни фактическое значение результата обработки этого символа (значение апостериорной вероятности или функции правдоподобия) в дальнейшем процессе приема (при декодировании) не принимаются во внимание. В то же время их учет мог бы привести к уменьшению вероятности ошибочного декодирования кодовой комбинации.

         Вся информация, содержащаяся в принимаемом сигнале, будет наиболее полно использована, если отказаться от посимвольного приема и демодулировать кодовую комбинацию в целом.

         Можно показать, что при использовании кода с избыточностью помехоустойчивость приема в целом выше помехоустойчивости поэлементного приема с исправлением ошибок, однако уступает помехоустойчивости поэлементного приема с обнаружением ошибок и переспросом по обратному каналу. При использовании кода без избыточности прием в целом не имеет преимуществ по сравнению с поэлементным приемом.

Рекомендуем посмотреть лекцию "11 Аннотирование цикла".

         В общем случае вычислить вероятность ошибочного приема кодовой комбинации трудно. Однако иногда, например, при использовании ортогональных, биортогональных и симплексных кодов, эту вероятность можно вычислить через интегралы, которые можно определить численными методами.

         Недостатком приема в целом является то, что он требует значительно более сложной аппаратуры по сравнению с поэлементным приемом. В частности, для его реализации требуется 2^k корреляторов. Очевидно, что при достаточно эффективном коде (такой код является длинным) прием в целом технически не реализуем. Так, если используется код (n, k) c k=10, то демодулятор, реализующий прием в целом, будет состоять из 1024 корреляторов или согласованных фильтров.

         В связи с трудностями построения оптимального демодулятора для приема в целом большое внимание уделяется алгоритмам приема, которые не используют всю информацию о принятом сигнале, но допускают меньшие потери по сравнению с поэлементным приемом. Такие алгоритмы являются двухэтапными, как и при поэлементном приеме. Однако на первом этапе решение о переданном символе не принимается, а запоминаются значения напряжений на выходах корреляторов или согласованных фильтров, предназначенных для приема различных символов, из которых составляются кодовые комбинации. Такой вид решения  называется "мягким". Как известно, эти напряжения пропорциональны логарифму функций правдоподобия и несут информацию о степени соответствия принятого сигнала тому или иному символу. Их использование при дальнейшей обработке (декодировании) и позволяет получить лучшие результаты по сравнению с поэлементным приемом.

         В реальных системах выходные напряжения обычно квантуются и представляются числами, т.е. вместо оптимального аналогового декодирования по максимуму правдоподобия используют цифровое декодирование. Цифровое декодирование уже при восьми уровнях квантования практически дает те же результаты, что и аналоговое декодирование. В то же время оно значительно проще в реализации.

         Существуют и другие методы приема, занимающие промежуточное положение между поэлементным приемом и приемом в целом, например, прием по наиболее надежным символам. В его основу положен тот факт, что при применении кода с кодовым расстоянием d любую его комбинацию можно декодировать, если "стереть" d-1 символов. Устройство приема состоит из двух решающих схем. Первая из них вычисляет апостериорные вероятности и принимает предварительно решение о переданном символе. Полученная последовательность символов подается на вторую решающую схему, куда также поступает  информация об апостериорных вероятностях. Декодирование выполняется по n-d+1 наиболее надежным (имеющим большие значения апостериорной вероятности) символам.

         Описанный метод дает лучшие результаты, чем поэлементный прием, так как в нем частично используется информация об апостериорных вероятностях, но уступает приему в целом, так как информация о d-1 менее надежных символах не используется.