Нелинейные детерминированные модели

2.4. Нелинейные детерминированные модели

Нелинейные детерминированные модели обладают бóльшей точностью и гибкостью. Они могут быть заданы в виде нелинейной функции одной или нескольких переменных или в виде дифференциальных уравнений (обыкновенных или в частных производных). Наиболее распространенными среди нелинейных моделей при описании ДУ и ДЛА являются:

– полиномиальные функции;

– позиномные функции;

– тригонометрические функции;

– экспоненциальные функции;

– обыкновенные дифференциальные уравнения;

– дифференциальные уравнения в частных производных др.

Нелинейные модели могут быть записаны в виде функционала, зависящего от управляющих переменных х и некоторых функций f(x) всех или части этих переменных:
W = W(x,f(x)). При этом функции f(x) могут представлять собой функционалы, зависящие от промежуточных функций f*(x) и т.д. На класс функций f(x), f*(x) не накладывается никаких ограничений, однако предполагается возможность однозначного перехода от вектора управляющих параметров х к общей характеристике модели W.

Область определения модели может быть ограничена с помощью равенств или неравенств:

Рекомендуемые материалы

x_i = c_i ,           i = 1,…, m;

f(x) = c_j ,         j = 1,…, l;

x_{i min} £ x_i £ x_{i max} , i = 1,…, k;

f_j(x) £ c_j ,        j = 1,…, n.

По существу под определение нелинейной модели подпадает любое математическое описание ДУ и ДЛА, не укладывающееся в рамки более простых моделей.

2.4.1. Полиномиальные модели

Полиномиальные модели основаны на идее приближенного представления модели конечным числом членов ряда Тейлора:

 .

Наиболее простой из моделей этого класса является квадратичная модель:

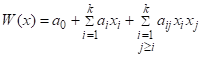
при ограничениях

          

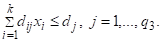
Квадратичные модели широко используются для представления экспериментальных данных при идентификации ДЛА и их элементов.

Квадратичные модели используются для аппроксимации отдельных участков поверхности отклика, когда линейное приближение оказывается недостаточным, например, в окрестности экстремума, и лежит в основе нелинейных методов оптимизации. Если квадратичная модель также оказывается недостаточно точной, то используются полиномиальные модели более высоких порядков.

Исследование полиномиальных моделей частично можно осуществить аналитическими методами. Например, аналитически можно определить степень влияния отдельных переменных на характеристики модели.

2.4.2. позиномные модели

Позиномные модели основаны на представлении модели в виде суммы произведений степенных функций:

,                               (2.14)

где x_i – управляющие переменные, a_ij – произвольные положительные числа, c_j ³ 0 – обеспечивает выпуклость модели.

Величины a_ij, с_j рассчитываются на основе статистических данных, отражающих опыт производства соответствующих узлов и систем.

Позиномные модели можно использовать для описания стоимости сложных систем.

К позиномным моделям сводится задача выбора геометрических характеристик ряда технических устройств, в том числе элементов ДЛА, например, электромагнитов, силовых ферм и т.д.

Исследование позиномных моделей сложнее, чем моделей полиномиального типа, и осуществляется в основном численными методами. Однако, при m = 1 и x₁ > 0, x₂ > 0,…, x_k > 0 в формуле (2.4) существует способ приведения позинома к линейному виду.

В этом частном случае модель (2.4) будет выглядеть в следующем виде:

.

Прологарифмируем обе части этого равенства, получим

.                                 (2.15)

Введем обозначения логарифмов переменных W, x₁, x₂,…,x_k и константы с:

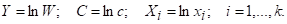
Выражение (2.5) примет линейный вид

Y(X₁, X₂,…, X_k)  = C + a₁x₁ + a₂x₂ + … +a_kx_k.

Для поиска оптимальных решений на основе позиномных моделей разработан специальный аппарат – так называемое геометрическое программирование.

2.4.3. Математическая модель кратчайшего пути

В качестве примера применения нелинейных статических моделей рассмотрим задачу описания двумерного движения точки по ограниченной области (рис. 2.8). Такая задача может возникнуть при определении координат опорных точек движения инструмента на станке с ЧПУ.

Найдем кратчайший путь от точки А с координатами (х_А, у_А) до точки В с координатами (х_В, у_В) на плоскости, из которой исключена область D, определенная неравенством   x² + y² £ R² .

Кратчайшим расстоянием между двумя точками на плоскости является соединяющий их отрезок прямой.

Пусть расстояние между точками А и В равно р и центр окружности, ограничивающий область D, лежит посередине между точками А и В. Тогда

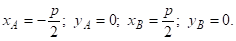
Рассмотрим путь АСВ, где точка С имеет координаты (0, у_С), а у_С – достаточно велико, чтобы отрезки АС и СВ не пересекались с областью D. Тогда по теореме Пифагора

.

Отсюда видно, что при убывании у_С путь сокращается. Будем уменьшать у_С до тех пор, пока АС не коснется окружности в точке Е₁ (С ® С₁). Этот путь является наилучшим среди путей, составленных из двух отрезков прямых линий.

Обозначим через a угол  ÐЕ₁0С₁, тогда  E₁C₁ + C₁F₁ = 2Rtga;

Длина дуги E₁F₁ определяется по формуле  arcE₁F₁ = 2Ra .

Но tga > a для всех a Î .

Следовательно, путь, состоящий из отрезка АЕ₁, дуги E₁F₁ и отрезка F₁B, является более коротким, чем АС₁В.

На этой стадии решения задачи мы выяснили, что кратчайший путь состоит их двух отрезков прямых линий и дуги окружности.

Для окончательного решения задачи рассмотрим путь АЕ₂ , дуга E₂F₂ , F₂B, где ÐА0Е₂ = ÐВ0F₂ = b.

Длину этого пути обозначим через S. Получим математическую модель пути:

.               (2.16)

,                                    (2.16')

где a – угол между прямой Е₁0 и осью 0Y.

Ограничение (2.16') вводится потому, что при  прямая АЕ₁ пересечет область D, а этого не должно быть.

Задача заключается в определении угла b₀, при котором путь S будет минимальным. Необходимым условием минимума функции S(b) является равенство нулю производной:

.                                                             (2.17)

Рассмотрим частный случай:

P = 4;  R = 1.

Тогда          .

Подставив значения p и R в математическую модель (2.6), получим

.

Произведя некоторые преобразования, получим

.

Возьмем производную по b от этого выражения и приравняем ее к нулю.

.

Получили уравнение, решив которое относительно b, найдем значение угла b₀, при котором S минимально. Опустив промежуточные преобразования, получим cosb = 1/2.
То есть b = p/3.

Чтобы убедиться, что найденное значение является точкой минимума, необходимо исследовать вторую производную от (2.16). Если она больше нуля при b = b₀, то S(b) действительно минимальна в этой точке.

Вторая производная от S(b) имеет вид

.

Подставив в нее найденное значение b₀ = p/3, получим

.

Равенство нулю второй производной требует дополнительного исследования критической точки. Необходимо найти первую, не обращающуюся в нуль, производную. Если она нечетного порядка, функция не имеет в исследуемой точке ни максимума, ни минимума. Если она четного порядка и больше нуля, исследуемая точка является минимумом. Проверим третью производную от S(b) по b:

.

Отсюда имеем, что при b = p/3 функция S(b) не имеет ни максимума, ни минимума. Действительно, из графика функции S(b) (рис. 2.9) видно, что на отрезке (2.16') функция (2.16) монотонно убывает. В точке b₀ = p/3, совпадающей с b_огр, кривая имеет точку перегиба. Наименьшее в области определения значение находится на границе этой области. следовательно, путь AE₁GF₁B действительно кратчайший и его длина равна S(p/3) = 4,511.

Покажем, что математическая модель (2.6) для любых p и R  монотонно убывает на отрезке  и, следовательно, имеет наименьшее значение при . Для этого необходимо показать, что вторая производная от S(b) на интересующем нас отрезке не превышает нуля.

Вторая производная от функции (2.6) имеет вид

.

Покажем, что она не превышает нуля:

.

Разделив обе части неравенства на 2R и умножив на корень квадратный (это можно сделать, не нарушив неравенства, так как R > 0, а корень квадратный представляет собой длину отрезка, т. е. тоже больше нуля), получим

.

Возведя обе части в квадрат (на рассматриваемом отрезке sin(b) > 0) и произведя некоторые преобразования, получим

.

В левой части неравенства cos²(b) можно заменить его минимальным значением, т.е. нулем, а в правой части – максимальным значением, т.е. единицей. Тогда получим

0 ³ 4pR – 4R²   или     p ³ R.

Но p действительно больше R (см. рис. 2.5).

Таким образом, аналитическую модель пути (формула (2.6)) мы использовали для доказательства того, что при b = p/2 – a путь является кратчайшим. Зная это, можно определить координаты опорных точек движения инструмента на станке с ЧПУ при любых значениях величин  p и R:

А(–р/2, 0); Е₁(–Rsin(a), Rcos(a)); F₁(Rsin(a), Rcos(a)); B(p/2, 0),

где a = .

Контрольные вопросы к лекции 4

1. Какие виды нелинейных математических моделей Вы знаете?

Лекция "1 Общество, политическая власть, государство" также может быть Вам полезна.

2. Приведите общий вид квадратичного полинома.

3. Приведите формулу позинома.

4. Как привести позином к линейному виду (при каком условии)?

5. К какому типу можно отнести модель кратчайшего расстояния между двумя точками?

6. Является ли найденное значение угла b точкой минимума пути?

7. Является ли путь S при найденном значении угла b кратчайшим?