Системы случайных величин
4. Системы случайных величин
4.1. Понятие о системе случайных величин
В практических применениях теории вероятностей очень часто приходится сталкиваться с задачами, в которых результат опыта описывается не одной случайной величиной, а двумя или более случайными величинами, образующими комплекс или систему. Условимся систему нескольких случайных величин 
обозначать 
.
Свойства системы нескольких случайных величин не исчерпываются свойствами отдельных величин, ее составляющих: помимо этого, они включают также взаимные связи (зависимости) между случайными величинами.
При рассмотрении вопросов, связанных с системами случайных величин, удобно пользоваться геометрической интерпретацией системы. Например, систему двух случайных величин 
можно изображать случайной точкой на плоскости с координатами Х и Y (рис. 4.1). Аналогично система трех случайных величин может быть изображена случайной точкой в трехмерном пространстве. Часто бывает удобно говорить о системе п, случайных величин как о «случайной точке в пространстве п измерений». Несмотря на то, что последняя интерпретация не обладает непосредственной наглядностью, пользование ею дает некоторый выигрыш в смысле общности терминологии и упрощения записей.
Рис. 4.1 Рис. 4.2
Часто вместо образа случайной точки для геометрической интерпретации системы случайных величин пользуются образом случайного вектора. Систему двух случайных величин при этом рассматривают как случайный вектор на плоскости хОy, составляющие которого по осям представляют собой случайные величины X, Y (рис. 4.2). Система трех случайных величин изображается случайным вектором в трехмерном пространстве, система п случайных величин – случайным вектором в пространстве п измерений. При этом теория систем случайных величин рассматривается как теория случайных векторов.
4.2. Функция распределения системы
двух случайных величин
Функцией распределения системы двух случайных величин называется вероятность совместного выполнения двух неравенств 
и 
:
. (4.1)
Если пользоваться для геометрической интерпретации системы образом случайной точки, то функция распределения 
есть не что иное, как вероятность попадания случайной точки в бесконечный квадрант с вершиной в точке 
, лежащий левее и ниже ее (рис. 4.3).
Рекомендуемые материалы
Рис. 4.3
Ранее были приведены основные свойства функции распределения F(х) для одной случайной величины. Сформулируем свойства для функции распределения системы случайных величин.
1. Функция распределения F(х, у) есть неубывающая функция обоих своих аргументов, т. е.
при 
;
при 
.
2. Повсюду на 
функция распределения равна нулю:
.
3. При одном из аргументов, равном 
функция распределения системы превращается в функцию распределения случайной величины, соответствующей другому аргументу:
,
где 
– соответственно функции распределения случайных величин Х и Y.
4. Если оба аргумента равны , функция распределения системы равна единице:
.
При рассмотрении законов распределения отдельных случайных величин приведено выражение для вероятности попадания случайной величины в пределы заданного участка. Эту вероятность выразили как через функцию распределения, так и через плотность распределения.
Аналогичным вопросом для системы двух случайных величин является вопрос о вероятности попадания случайной точки
в пределы заданной области D на плоскости хОy (рис. 4.4).
Рис. 4.4
Условимся событие, состоящее в попадании случайной точки в область D, обозначать символом 
.
Вероятность попадания случайной точки в заданную область выражается наиболее просто в том случае, когда эта область представляет собой прямоугольник со сторонами, параллельными координатным осям.
Выразим через функцию распределения системы вероятность попадания случайной точки в прямоугольник R, ограниченный абсциссами a и b и ординатами g и d (рис. 4.5).
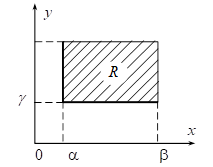
Рис. 4.5
При этом следует условиться, куда мы будем относить границы прямоугольника. Условимся включать в прямоугольник R его нижнюю и левую границы и не включать верхнюю и правую. Тогда событие 
будет равносильно произведению двух событий: 
и 
. Выразим вероятность этого события через функцию распределения системы. Для этого рассмотрим на плоскости хОу четыре бесконечных квадранта с вершинами в точках 
; 
; 
и 
(рис. 4.6).
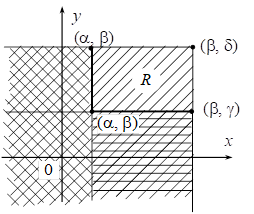
Рис. 4.6
Очевидно, вероятность попадания в прямоугольник R равна вероятности попадания в квадрант 
минус вероятность попадания в квадрант 
, минус вероятность попадания в квадрант 
, плюс вероятность попадания в квадрант 
(т. к. мы дважды вычли вероятность попадания в этот квадрант). Отсюда получаем формулу, выражающую вероятность попадания в прямоугольник через функцию распределения системы:
. (4.2)
В дальнейшем, когда будет введено понятие плотности распределения системы, мы выведем формулу для вероятности попадания случайной точки в область произвольной формы.
4.3. Плотность распределения системы
двух случайных величин
Функция распределения существует для систем любых случайных величин, как прерывных, так и непрерывных. Основное практическое значение имеют системы непрерывных случайных величин. Распределение системы непрерывных величин обычно характеризуют не функцией распределения, а плотностью распределения.
Предположим, что функция 
не только непрерывна, но
и дифференцируема; тогда вторую смешанную частную производную функции по х и у, обозначим 
:
. (4.3)
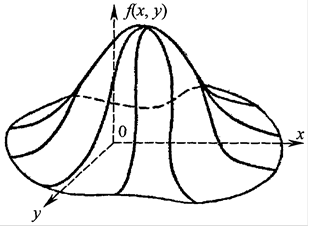
Рис. 4.7
Функция называется плотностью распределения системы.
Если воспользоваться «механической» интерпретацией распределения системы как распределения единичной массы по плоскости хОу, то функция представляет собой плотность распределения массы в точке .
Геометрически функцию можно изобразить некоторой поверхностью. Эта поверхность аналогична кривой распределения для одной случайной величины и называется поверхностью распределения (рис. 4.7).
4.4. Числовые характеристики системы
двух случайных величин
Ранее рассматривались числовые характеристики одной случайной величины X – начальные и центральные моменты различных порядков. Из этих характеристик важнейшими являются две: математическое ожидание тх и дисперсия Dх.
Аналогичные числовые характеристики – начальные и центральные моменты различных порядков – можно ввести и для системы двух случайных величин.
Начальным моментом порядка k, s системы (X, Y) называется математическое ожидание произведения 
на 
:
. (4.4)
Центральным моментом порядка k, s системы (X, Y) называется математическое ожидание произведения k-й и s-й степени соответствующих центрированных величин:
, (4.5)
где 
, 
.
Выпишем формулы, служащие для непосредственного подсчета моментов. Для прерывных случайных величин
, (4.6)
, (4.7)
где 
– вероятность того, что система (X, Y) примет значения 
, а суммирование распространяется по всем возможным значениям случайных величин X, Y.
Для непрерывных случайных величин:
, (4.8)
, (4.9)
где – плотность распределения системы.
Помимо чисел k и s, характеризующих порядок момента по отношению к отдельным величинам, рассматривается еще суммарный порядок момента 
, равный сумме показателей степеней при X и Y. Соответственно суммарному порядку моменты классифицируются на первые, вторые и т. д. На практике обычно применяются только первые и вторые моменты.
Первые начальные моменты представляют собой уже известные нам математические ожидания величин X и Y, входящих в систему:
,
.
Совокупность математических ожиданий mх, my представляет собой характеристику положения системы. Геометрически это координаты средней точки на плоскости, вокруг которой происходит рассеивание точки .
Кроме первых начальных моментов на практике широко применяются еще вторые центральные моменты системы. Два из них представляют собой уже известные нам дисперсии величин X и Y:
,
,
характеризующие рассеивание случайной точки в направлении осей Ох и Оу.
Особую роль как характеристика системы играет второй смешанный центральный момент:
,
т. е. математическое ожидание произведения центрированных величин.
Ввиду того, что этот момент играет важную роль в теории систем случайных величин, введем для него особое обозначение:
. (4.10)
Характеристика Kху называется корреляционным моментом (иначе – «моментом связи») случайных величин X, Y.
Для прерывных случайных величин корреляционный момент выражается формулой
, (4.11)
а для непрерывных – формулой
. (4.12)
Корреляционный момент есть характеристика системы случайных величин, описывающая, помимо рассеивания величин X и Y, еще и связь между ними. Для независимых случайных величин корреляционный момент равен нулю.
Если корреляционный момент двух случайных величин отличен от нуля, это есть признак наличия зависимости между ними.
Корреляционный момент характеризует не только зависимость величин, но и их рассеивание. Действительно, если, например, одна из величин (X, Y) весьма мало отклоняется от своего математического ожидания (почти не случайна), то корреляционный момент будет мал, какой бы тесной зависимостью ни были связаны величины . Поэтому для характеристики связи между величинами в чистом виде переходят от момента 
к безразмерной характеристике
, (4.13)
где 
– средние квадратические отклонения величин X, Y.
Эта характеристика называется коэффициентом корреляции величин X и Y. Очевидно, коэффициент корреляции обращается
в нуль одновременно с корреляционным моментом; следовательно, для независимых случайных величин коэффициент корреляции равен нулю.
Случайные величины, для которых корреляционный момент (а значит, и коэффициент корреляции) равен нулю, называются некоррелированными (иногда – «несвязанными»).
Бесплатная лекция: "37 Образование политических партий" также доступна.
Выясним, эквивалентно ли понятие некоррелированности случайных величин понятию независимости. Две независимые случайные величины всегда являются некоррелированными. Выясним: справедливо ли обратное положение, вытекает ли из некоррелированности величин их независимость? Оказывается – нет. Можно построить примеры таких случайных величин, которые являются некоррелированными, но зависимыми. Равенство нулю коэффициента корреляции – необходимое, но не достаточное условие независимости случайных величин. Из независимости случайных величин вытекает их некоррелированность; напротив, из некоррелированности величин еще не следует их независимость. Условие независимости случайных величин – более жесткое, чем условие некоррелированности.
Коэффициент корреляции характеризует не всякую зависимость, а только так называемую линейную зависимость. Линейная вероятностная зависимость случайных величин заключается в том, что при возрастании одной случайной величины другая имеет тенденцию возрастать (или же убывать) по линейному закону. Эта тенденция к линейной зависимости может быть более или менее ярко выраженной, более или менее приближаться к функциональной, т. е. самой тесной линейной зависимости. Коэффициент корреляции характеризует степень тесноты линейной зависимости между случайными величинами. Если случайные величины X и Y связаны точной линейной функциональной зависимостью:
,
то 
, причем знак «плюс» или «минус» берется в зависимости от того, положителен или отрицателен коэффициент а. В общем случае, когда величины X и Y связаны произвольной вероятностной зависимостью, коэффициент корреляции может иметь значение в пределах:
.
В случае 
говорят о положительной корреляции величин X и Y, в случае 
– об отрицательной корреляции. Положительная корреляция между случайными величинами означает, что при возрастании одной из них другая имеет тенденцию в среднем возрастать; отрицательная корреляция означает, что при возрастании одной из случайных величин другая имеет тенденцию в среднем убывать.
