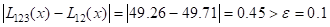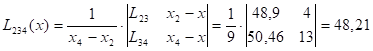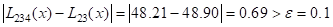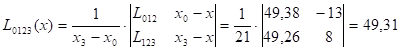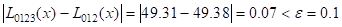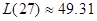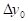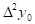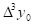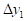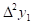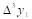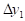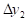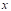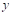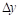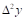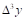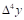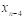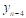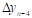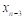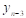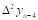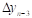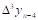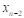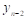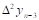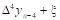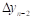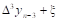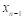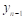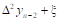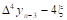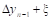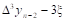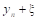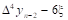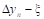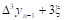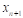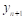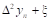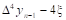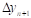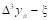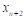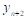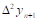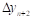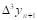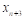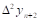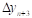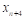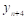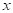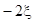Интерполяция функций
Интерполяция функций.
Первый этап работы любого вычисления - числа, приближения, погрешность.
Второй этап работы - функция, вычисления функции, её приближения. В краце о интерполяции. Интерполяция в простейшем случае заключается в следующем:
 Существует какая-то функция, на ней заданы точки (называемые узлами интерполяции), требуется построить (интерполированную) функцию, которая принимала бы в указанных узлах те же значения.
Существует какая-то функция, на ней заданы точки (называемые узлами интерполяции), требуется построить (интерполированную) функцию, которая принимала бы в указанных узлах те же значения.
Постановка задачи.
На отрезке  заданы n значений аргумента x и соответствующие им значения функции f(x0)=y0; f(x1)=y1; …; f(xn)=yn.
заданы n значений аргумента x и соответствующие им значения функции f(x0)=y0; f(x1)=y1; …; f(xn)=yn.
Требуется построить функцию F(x), которая бы принимала в точках x те же значения, что и f(x):
F (x0)=y0; F (x1)=y1… F (xn)=yn
Рекомендуемые материалы
Для чего?
Для того, чтобы:
1. Задача интерполяции. Суметь по полученной функции вычислить значения F(z), где z
 ,
,
z xi при i=0,n
xi при i=0,n
2. Задача экстраполяции. Суметь по полученной функции вычислить F(z), где z
 .
.
Все существующие интерполяционные формулы содержат в себе конечные разности различных порядков.
Введём понятие конечных разностей.
Конечные разности различных порядков.
Пусть: y =f(x) - заданная функция
 - фиксированная величина приращения аргумента
- фиксированная величина приращения аргумента
Тогда  - называется первой конечной разностью функции y, или конечной разностью первого порядка.
- называется первой конечной разностью функции y, или конечной разностью первого порядка.
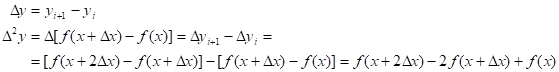
Вторая конечная разность, или конечная разность второго порядка.

Третья конечная разность, или конечная разность третьего порядка.
Т.о., в общем виде:
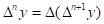
Конечная разность n-го порядка.
Пример: 
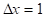
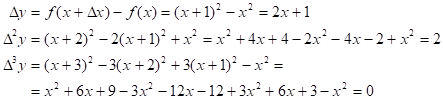
Конечные разности различных порядков удобно располагать в форме таблиц двух видов: горизонтальной и диагональной таблиц разностей
| x | y |
|
|
|
| x0 | y0 |
|
|
|
| x1 | y1 |
|
|
|
| ... | ... | ... | ... | ... |
Диагональная таблица разностей.
| x | y |
|
|
|
| X0 | Y0 | |||
|
| ||||
| X1 | Y1 |
| ||
|
|
| |||
| X2 | Y2 |
| ||
|
| ||||
| X3 | Y3 |
Пример: горизонтальная таблица функции y = f(x) = x2 при
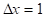 , x0 = 0 начальное значение, x6=5 конечное значение
, x0 = 0 начальное значение, x6=5 конечное значение
| x | y |
|
|
|
| 0 | 0 | 1 | 2 | 0 |
| 1 | 1 | 3 | 2 | 0 |
| 2 | 4 | 5 | 2 | 0 |
| 3 | 9 | 7 | 2 | |
| 4 | 16 | 9 | ||
| 5 | 25 |
Диагональная таблица
| x | y |
|
|
|
| 0 | 0 | |||
| 1 | ||||
| 1 | 1 | 2 | ||
|
|
| 3 | 0 | |
| 2 | 4 |
| 2 | |
|
|
| 5 |
| |
| 3 | 9 |
|
|
|
При составлении таблиц возможные ошибки вычисляются и диагональная таблица наглядно показывает нам, как отразится ошибка  в значении yn.
в значении yn.
|
|
|
|
|
|
|
|
|
| ||||
|
| |||||
|
|
|
| |||
|
|
| ||||
|
|
|
|
| ||
|
|
| ||||
|
|
|
|
| ||
|
|
| ||||
|
|
|
|
| ||
|
|
| ||||
|
|
|
|
| ||
|
|
| ||||
|
|
|
|
| ||
|
|
| ||||
|
|
|
| |||
|
| |||||
|
|
|
Следует заметить, что максимальная ошибка  – в той же горизонтальной строке, где и табличная величина yn.
– в той же горизонтальной строке, где и табличная величина yn.
Пример: исправить ошибку в таблице (неверные цифры взяты в скобки).
|
|
|
|
| Ошибка |
| 15 | 13,260 | 0 | ||
| 884 | ||||
| 16 | 14,144 | 0 | ||
| 884 | ||||
| 17 | 15,912 | 0 | ||
| 884 | ||||
| 18 | 15,028 | (-4)0 | ||
| 88(0)4 | ||||
| 19 | 16,79(2)6 | (8)0 |
| |
| 88(8)4 | ||||
| 20 | 17,680 | (-4)0 |
| |
| 884 | ||||
| 21 | 18,564 | 0 |
| |
| 884 | ||||
| 22 | 19,448 | 0 | ||
| 884 | ||||
| 23 | 20,332 | 0 |
Как видно из таблицы, ход вторых разностей нарушается при x=19. Ошибка распространяется на 3 строки. Находим среднее арифметическое значение второй разности для средней из 3 точек:
 =
= ,
,  =
=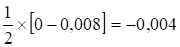
Внося исправление в табличное значение y для x=19, получим верное значение функции:
 n=(yn+
n=(yn+  )-
)-  =16.792-(-0.004)=16.796.
=16.792-(-0.004)=16.796.
Первая интерполяционная формула Ньютона.
Пусть для функции y=f(x) заданы значения yi=f(xi) для равноотстоящих значений независимой переменной xi=x0+i*h (i=0,n) , где h - шаг интерполяции.
Требуется подобрать полином Pn(x) степени не выше n, принимающий в точках xi значения Pn(xi)=yi (i=0,n)
Ньютон решил поставленную задачу:
Pn(x)=y0+q y+
y+ +
+ y0,
y0,
где q= .
.
Эта формула называется первой интерполяционной формулой Нью-тона.
 Каков физический смысл имеет переменная q в первой интерполяционной формулой Ньютона.
Каков физический смысл имеет переменная q в первой интерполяционной формулой Ньютона.
q= ,
,
где k - число шагов, необходимых для достижения точки x , исходя из точки x0.
Рассмотрим частные случаи n=1 или n=2:
n=1 P1(x)=y0+q y0 – линейное интерполирование
y0 – линейное интерполирование
n=2 P2(x)=y0+q y0+
y0+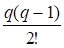
 2y0–параболическое (квадратичное) интерполирование
2y0–параболическое (квадратичное) интерполирование
Пример: необходимо построить интерполяционный полином Ньютона для функции y= на отрезке
на отрезке  c h=1
c h=1
| X | 4 | 5 | 6 | 7 | 8 |
| Y | 0.25 | 0.2 | 0.167 | 0.143 | 0.125 |
Горизонтальная таблица разностей.
| x | y |
|
|
|
|
| 4 | 0.25 | -0.05 | 0.017 | -0.008 | 0.005 |
| 5 | 0.2 | -0.033 | 0.009 | -0.003 | |
| 6 | 0.167 | -0.024 | 0.006 | ||
| 7 | 0.143 | -0.018 | |||
| 8 | 0.125 |
Т.о., при наличии 5 точек максимальный порядок существующей конечной разности =4, максимальная степень полинома =4.
P4(x)=y0+q y0+
y0+ +
+ y0+
y0+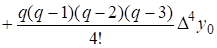
Как пользоваться формулой?
Допустим, необходимо определить значение в точке x=4.4
Узловые точки x0=4, h=1,тогда q=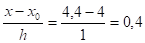
 Точное значение =0.22727.
Точное значение =0.22727.
Вторая интерполяционная формула Ньютона.
Первая интерполяционная формула Ньютона практически неудобна для интерполирования значений вблизи конца таблицы. В этом случае обычно применяется вторая интерполяционная формула Ньютона.
Pn(x)=yn+q yn-1+
yn-1+ +
+ y0,
y0,
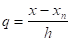
Пример: y= sin x x , h=5
, h=5
Горизонтальная таблица разностей.
| x | y |
|
|
|
|
|
| 30 | 0.5000 | 0.0736 | -0.0044 | -0.0005 | 0 | 0.0002 |
| 35 | 0.5736 | 0.0692 | -0.0049 | -0.0005 | 0.0002 | |
| 40 | 0.6428 | 0.0643 | -0.0054 | -0.0003 | ||
| 45 | 0.7071 | 0.0589 | -0.0057 | |||
| 50 | 0.7660 | 0.0532 | ||||
| 55 | 0.8192 |
Пример: Отыщем sin(51 o), xn=51, x=50o, q=0.2
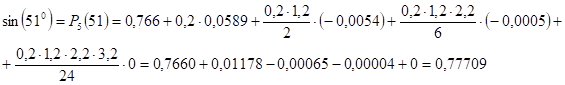
Как первая, так и вторая формула Ньютона может быть использована для экстраполирования функции, т.е. для нахождения значений функции y для значений аргументов x, лежащих вне пределов таблицы.
Если x<x0, то лучше применять первую интерполяционную функцию Ньютона.
Если x>x0, то лучше применять вторую интерполяционную функцию Ньютона.
Т.е., 1ИФН используется для интерполирования вперёд и экстраполирования назад.
2 ИФН используется для интерполирования назад и экстраполирования вперёд.
Как видно из формул 1 и 2 , при интерполяции используется разности: в 1ИФН  ny0 , во 2ИФН
ny0 , во 2ИФН  kyk+_ .
kyk+_ .
Но существуют формулы, называемые формулы с центральными разностями, к ним относятся:
- ИФ Гаусса
- ИФ Стерлинга
- ИФ Бесселя,
которые используют разности, расположенные в горизонтальной строке диагональной таблицы, соответствует начальным значениям xk, yk или в строках близлежащих.
Но все эти формулы работают только для постоянного шага.
Необходимо отметить следующее:
при построении интерполяционных формул Ньютона в качестве начального значения  выбирается первый или последний узел интерполирования; для центральных формул начальный узел является средним.
выбирается первый или последний узел интерполирования; для центральных формул начальный узел является средним.
При  применяют формулу Стирлинга, а при
применяют формулу Стирлинга, а при  - Бесселя.
- Бесселя.
1ИФН и 2ИФН применяют тогда, когда интерполирование производится в начале или в конце таблицы и нужных центральных разностей не хватает.
Общая характеристика интерполяционных
формул с постоянным шагом.
Может быть представлена в виде диагональной таблицы разностей:
| x | y |
|
|
|
| Примечание |
| x-2 | y-2 |
|
|
|
| 2-я ИФН |
|
|
|
|
|
|
|
|
| x-1 | y–1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
| x0 | y0 |
|
|
|
| ф. Стерлинга |
|
|
|
|
|
|
| ф. Бесселя |
| x1 | y1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
| x2 | y2 |
|
|
|
| 1-я ИФН |
Мы рассмотрели интерполяционные формулы для равностоящих узлов интерполирования.
Рассмотрим формулы для произвольно заданных узлов интерполирования.
Наиболее часто используется формула Лагранжа.
Интерполяционная формула Лагранжа.
Пусть на отрезке [a;b] даны n+1 различных значений аргумента x: x0, x1,…, xn и известны соответствующие их значению функции y=f(x) : f(x0)=y0, f(x1)=y1, f(xn)=yn. Требуется построить полином  степени не выше
степени не выше  , имеющий в заданных узлах
, имеющий в заданных узлах  те же значения, что и функция
те же значения, что и функция  , т.е. Ln(xi)=yi при i=1,n
, т.е. Ln(xi)=yi при i=1,n
 ;
;
 ,
,
где Li(n)- коэффициенты Лагранжа.
Следует отметить, если узлы равностоящие, то интерполяционный полином Лагранжа совпадает с интерполяционной формулой Ньютона.
Примечательно то, что формула Лагранжа зависит лишь от yi, а не от разностей.
Частные случаи.
n=1
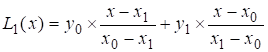
При n=1 имеем 2 точки: (x0;y0) и (x1;y1).
прямая, проходящая через эти точки-
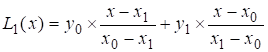
n=2 (x0;y0), (x1;y1), (x2;y2)
 Пример:
Пример:
|
|
|
|
| 0 | 0 | 2 |
| 1 | 1 | 3 |
| 2 | 2 | 12 |
| 3 | 5 | 147 |
 L3(x)=x3+x2-x+2
L3(x)=x3+x2-x+2
Для вычисления лагранжевых подмножеств удобно составлять следующую таблицу разности:
| x-x0 | x0-x1 | x0-x2 | ….. | x0-xn |
| x1-x0 | x-x1 | x1-x2 | ….. | x1-xn |
| x2-x0 | x2-x1 | x-x2 | ….. | x2-x1 |
| ….. | ….. | ….. | ….. | ….. |
| xn-x0 | xn-x1 | xn-x2 | ….. | x-xn |
Обозначим произведение элементов i-ой строки через Di , а произведение главной диагонали Пn+1(x). Отсюда следует, что:
Пn+1(x)=(x-x0)(x-x1)…(x-xn)
 при i=1,n
при i=1,n
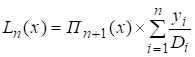
Для упрощения вычислений можно использовать инвариантность (при равноотстоящих точках лагранжевых коэффициентов),если
x= at+b
xj= atj+b при j=0,n
то Li(n)(x)= Li(n)(t)
Схема Эйткена
Чаще всего требуется найти не общее выражение Ln(x) , а значение его при конкретных x , тогда будет удобно пользоваться интерполяционной схемой Эйткена:
Последовательно вычисляются многочлены:
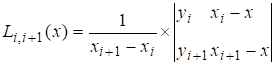
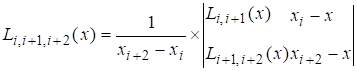
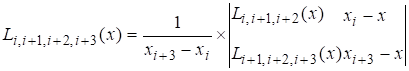
и т.д.

Вычисления по схеме Эйткена удобно расположить в таблице:
| Xi | Yi | Xi-X | Li-1,i | Li-2,i-1,i | Li-3,i-2,i-1,i |
| X0 | Y0 | X0-X | L01 | L012 | L0123 |
| X1 | Y1 | X1-X | L12 | L123 | L1234 |
| X2 | Y2 | X2-X | L23 | L234 |
|
| X3 | Y3 | X3-X | L34 |
|
|
| X4 | Y4 | X4-X |
|
|
|
Вычисления по схеме Эйткена обычно ведутся до тех пор, пока последовательные значения L01…n(x) и L01…n(n+1) не совпадут по заданной точности.
Т.е. процедура является итерационной, легко реализуется и этим обеспечивает возможность автоматического контроля точности вычислений.
Пример: x=27,  =0,1
=0,1
| i | xi | yi | xi-x | Li-1,i | Li-2,i-1,i | Li-3,i-2,i-1,i | Li-4,i-3,i-2,i-1,i |
| 0 | 14 | 68,7 | -13 | 48,33 | 49,38 | 49,31 | |
| 1 | 17 | 64,0 | -10 | 49,71 | 49,26 | ||
| 2 | 31 | 44,0 | 4 | 48,90 | 48,21 | ||
| 3 | 35 | 39,1 | 8 | 50,46 | |||
| 4 | 40 | 32,0 | 13 |
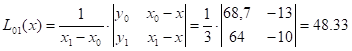
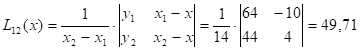
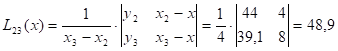
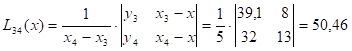
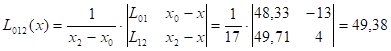
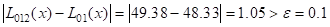
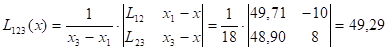
Лекция "60 Внутришлифовальный станок модели за252" также может быть Вам полезна.