Хаос в простых моделях динамических систем

ГЛАВА IV. Хаос в простых моделях динамических систем

                             Основные определения

Одно из фундаментальных понятий, изучаемых в нашем курсе, – это понятие динамической системы. О динамической системе говорят в том слу­чае, если можно ука­зать такой набор величин, называемых динамическими перемен­ными и характеризующих состояние системы, что их значения в лю­бой последующий момент времени получаются из исходного набора по оп­ределенному правилу. Это правило задает оператор эволюции системы. Если состояние системы задается набором N величин, то изменение состояния во времени, или динамику системы, можно представить как движение точки по траектории в N-мерном фазовом пространстве, которую называют фазовой траекторией.

Когда-то в понятие динамической системы вкладывали чисто механи­ческое содержание, имея в виду набор тел, связанных си­ловыми взаимодей­ствиями и подчиняющихся системе дифферен­циальных уравнений, выте­кающих из законов Ньютона. По мере развития науки понятие динамической системы становилось ши­ре, охватывая объекты разной природы. Современ­ное понятие ди­намической системы это результат длительной эволюции на­учных представлений и синтеза достижений многих дисциплин. Оно под­ра­зумевает возможность задания оператора эволюции любым спо­собом, не обязательно дифференциальным уравнением. В последнее время и в теоретических исследованиях, и в рабо­тах прикладного характера рассматривают системы с дискретным временем, называемые каскадами (в отличие от динамических систем с непрерывным временем, называемых потоками), которые описываются рекуррентными ото­бражениями. В этом случае под фазовой траекторией сле­дует пони­мать некоторую дискретную последовательность точек в фазовом пространстве.

Выделяют два класса динамических систем – консервативные и дисси­пативные.

В физике свойство консервативности понимается как сохране­ние энер­гии. В частности, механические колебательные системы в отсутствие трения относятся к консервативным системам. В при­сутствии трения механическая энергия не сохраняется, а посте­пенно рассеивается (диссипирует) и перехо­дит в тепло, т. е., в энергию микроскопического движения молекул, состав­ляющих си­стему и ее окружение. Строго говоря, в этом случае временная эво­люция должна определяться не только состоянием самой системы, но и окружением. Все же и в этой ситуации описание в рамках концепции дина­мических систем, заданных, например, диффе­ренциальными уравнениями, очень часто оказывается разумным и достаточно точным. Это будет уже дис­сипативная динамическая система.

Пусть есть некоторая динамическая система, т.е., за­дано фазовое пространство и указан оператор эволюции. Вместо одной системы рассмот­рим ансамбль, состоящий из большого ко­личества ее идентичных копий, причем все представители ансам­бля могут отличаться друг от друга только лишь начальными усло­виями. В фазовом пространстве ансамбль представля­ется облаком изображающих точек. С течением времени каждая изображаю­щая точка перемещается в фазовом пространстве, как предписано ди­намиче­скими уравнениями системы, так что форма облака и его размеры будут ме­няться.

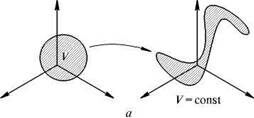
Может случиться, что объем облака в процессе временной эво­люции будет оставаться постоянным. Это характерно для консервативных систем, к которым относятся, в частности, рассматриваемые в классической механике гамильтоновы си­стемы.

Рекомендуемые материалы

Что касается диссипативных систем, то для них характерно, что с тече­нием времени облако изображающих точек «съежива­ется» и концентриру­ется в итоге на одном или нескольких ат­тракторах – подмножествах фазо­вого пространства, обладаю­щих обычно нулевым фазовым объемом. С точки зрения динамики во времени, это означает, что режим, возни­кающий в системе, предоставленной самой себе в течение длительного вре­мени, становится не зависящим от начального состояния (по край­ней мере, при вариации начальных условий в некоторых конечных пределах). 

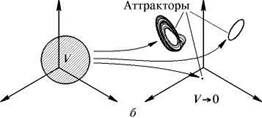
Простые примеры аттракторов – устойчивое состояние рав­новесия и устойчивый предельный цикл – замкнутая фазовая траектория, к которой стремятся с течением времени все близкие траектории. Предельный цикл от­вечает, как известно, режиму пе­риодических автоколебаний.

При наличии в фазовом пространстве двух или более аттрак­торов гово­рят, что имеет место, соответственно, бистабильность или мулътистабиносmъ. Множество точек фазового простран­ства, из которых траектории приходят в конце концов к какому-то одному аттрактору, называ­ется бассейном этого аттрактора.

Одним из важных понятий теории динамических систем явля­ется по­нятие инвариантного множества. Множество точек фа­зового пространства называют инвариантным в том случае, если фазовая траектория, стартующая из любой его точки, целиком при­надлежит этому множеству. Любой аттрак­тор есть инвариантное множество, но не наоборот. Неустойчивые неподвиж­ные точки, не­устойчивые замкнутые орбиты – это тоже инвариантные мно­же­ства.

Следует осознавать, что понятие динамической системы есть теоретическая абстракция, так же как многие другие при­вычные и полезные научные абстракции (материальная точка, аб­солютно твердое тело, несжи­маемая жидкость, идеальный газ). Реальные объекты могут рассматриваться как динамические си­стемы только в определенном приближении, в той мере, в какой при описании динамики можно игнорировать тонкие детали вну­т­ренней структуры системы и ее взаимодействие с окружающим миром.

Успехи классической механики в XVII–XIX вв. были столь впечат­ляющими, что стало казаться возможным представлять себе всю Вселенную как одну гигантскую динамическую систему. Эту позицию четко сформули­ровал Лаплас: «Состояние системы при­роды в настоящем есть, очевидно, следствие того, каким оно было в предыдущий момент, и если мы предста­вим себе разум, который в данное мгновение постиг все связи между объек­тами Вселенной, то он сможет установить соответствующие положения, движения и общие воздействия этих объектов в любое время в прошлом или в будущем» (1776 год). Эта доктрина, получившая название лапласовского детерминизма, выразила в концентрированном виде идеал научного позна­ния, каким он виделся в те времена. Понадо­бился длительный путь развития науки и научного мировоззрения (теория поля, термодинамика и статистиче­ская физика, квантовая механика), чтобы убедиться в несостоятельности та­кого предста­вления о мире.

Идеал лапласовского детерминизма прин­ципи­ально недостижим даже в том случае, если ограничиться рам­ками абстракции динамических систем. Феномен, ярко демон­стрирующий это обстоятельство, был открыт и стал общеизвест­ным в последние несколько десятилетий – это динамический хаос. Хаоти­ческие режимы характеризуются нерегулярным, похожим на слу­чайный процесс, изменением динамических переменных во вре­мени. В дис­сипативных системах хаос ассоциируется с нали­чием в фазовом простран­стве странных аттракторов – сложно устроенных фрактальных множеств, притягивающих к себе все траектории из некоторой прилегающей области –бассейна аттрак­тора.

Возможность хаотического поведения кажется на первый взгляд несо­вместимой с самим определением динамической си­стемы, основанном на ут­верждении о возможности однозначного предсказания конечного состояния по исходному. Цель настоящего курса – пока­зать, что упомянутое противоречие только кажущееся, и продемонстрировать присут­ствие хаоса в динамических системах. Для этого обра­тимся к моделям, представляющим собой искусственно сконстру­ированные «игрушечные» примеры, которые, во-первых, предста­вляют собой динамические системы в смысле общего опре­деления, во-вторых, допускают детальный теоретический анализ и, в-третьих, демонстри­руют хаотическое поведение.

Одномерные отображения

Рассмотрим модельные системы, состояние которых характе­ризуется единственной переменной Х, т. е., фазовое пространство од­номерно, а оператор эволюции задается рекуррент­ным отображением вида , где n – дискретное время.

Отображение «зуб пилы». Рассмотрим систему, оператор эво­люции которой задан следующим правилом определения нового состояния по пре­дыдущему:

                                                                                             

где фигурные скобки обозначают дробную часть числа. В другой общеупот­ребительной форме это соотношение записывают как

                                                                                 

Это дина­мическая система, заданная одномерным ре­куррентным отображе­нием.  На рисунке показан график отображения и по­строена итерационная диаграмма, иллюстрирующая несколько первых шагов динамики, начиная с некоторого начального состояния.

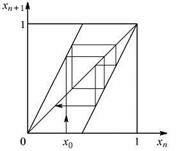
Пусть в качестве начального состояния выбрано некоторое чи­сло x₀, принадлежащее интервалу от 0 до 1. Запишем это число в двоичной системе счисления:

                    x₀ = 0,01011010001010011001010...

Теперь один шаг эволюции во времени согласно уравнению (2.1) или (2.2) состоит в том, что последовательность нулей и единиц сдвигается влево на одну позицию, и цифра, оказавшаяся по левую сторону от запятой, отбрасы­вается. Имеем:

                   x₁ = 0,1011010001010011001010...

                   x₂ = 0,011010001010011001010 ...

                   x₃ = 0,11010001010011001010 ...

и т. д. Ясно, что присутствие цифры 0 или 1 на первой позиции после запятой показывает, в какой половине единичного интер­вала – левой или правой пребывает динамическая переменная x_n в данный момент.

Что же следует из такого представления динамики. Предположим сначала, что двоичная дробь периодическая, это будет так, если х₀ рациональное число. Ясно, что состояние си­стемы будет перио­дически повторять исходное через число вре­менных шагов, равное периоду двоичного кода х₀. Такой харак­тер движения будет соответствовать любому рациональному чи­слу, а эти числа, как известно, образуют на единичном ин­тервале бесконечное счетное множество. Следовательно, система обладает бесконечным счетным множеством периодических орбит (циклов).

Непериодические двоичные дроби, отвечающие иррациональ­ным чис­лам x₀, образуют множество с мощностью континуума. Следовательно система имеет конти­нуум непериодических траек­торий.

Возможно задать начальное условие числом, имеющим произ­вольную последовательность нулей и единиц в своей двоичной записи. Возьмем слу­чайную последовательность, которую можно получить подбрасыванием мо­неты, записывая результаты испыта­ний по правилу орел – 0, решка – 1: 010010... Тогда при зада­нии начального состояния х₀ = 0,010010... динамиче­ская система в процессе своей эволюции будет посещать левую и пра­вую половину единичного интервала, следуя нашей случайной последова­тельности. Получим хаос, причем, в системе, описывае­мой детерминирован­ным уравнением.

Преобразование двоичной последовательности, состоящее в сдвиге всех ее символов на одну позицию, называют сдвигом Бер­нулли. (По ассо­циации с известной в теории вероятности схемой Бернулли, которая заклю­чается в последовательности независи­мых испытаний, когда каждое испыта­ние имеет два возможных исхода с вероятностями р и 1-р.)

Предположим теперь, что взято очень близкое, но другое начальное значение х₀. Очень близкое – это значит, что доста­точно большое количе­ство цифр двоичной записи до некоторой по­зиции, например 25-й, совпадает, а дальнейшие цифры («хвост») какие-то совсем иные. Тогда после 25 вре­менных шагов, т. е., сдвигов Бернулли, начало хвоста как раз придвинется к разде­лительной запятой. Дальнейшая динамика и последовательность посе­щений левой и правой половины единичного интервала бу­дет определяться структурой хвоста и, следовательно, будет совер­шенно другой, нежели это имело место для исходного начального условия. Таким образом, имея воз­можность контролировать точ­ность задания начального условия до 25-го двоичного знака, мы можем правильно предсказывать попадание x_n в левую или пра­вую половину единичного интервала лишь на протяжении первых 25 временных шагов.

Если динамическая система, подобная по своим свойствам рас­сматри­ваемой модели, привлекается для описания какой-либо фи­зически реали­стичной ситуации, то попытка предсказания состояния на N шагов вперед сталкивается при увеличении N с не­обходимостью столь точного задания на­чальных условий, что это становится в конце концов принципиально невоз­можным.

Логистическое отображение. Обратимся к следующему приме­ру – логистическому отображению

                                              ,

где х_n – динамическая переменная, a λ – параметр, от величины которого зависит характер динамики. Это тоже искусственно скон­струированная мо­дель динамической системы, но она имеет до­статочно реалистичную интер­претацию в биологии для описания динамики численности некоторых

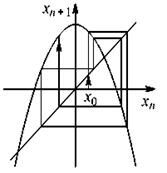
биологических популяций. Логистическое отображение может быть представлено в виде   , обе формы записи эквивалентны и сводятся друг к другу заменой переменной и параметра:

                        ,  .

Рассмотрим хаос в логистическом отображении, следуя заме­чательно простой идее, развитой в конце 40-х годов Уламом и фон Нейманом. Их под­ход применим при частном значении параметра λ = 2. В отображении, которое принимает вид

                                                                     (*)    

выполним замену переменной

                                                                                

После подстановки выражения указанного вида для x_n+1 и х_n в правую и ле­вую часть уравнения получаем

                          .

Используя соотношение   , 

получим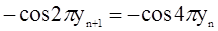                     

Это соотношение справедливо для всех n, если потребовать, чтобы пе­ременная у_n удовлетворяла рекуррентному уравнению

                                  .                            (**)      

Последовательность  будет подчиняться исходному уравнению (*). Соотношение (**) по сути – исследованное в предыдущем разделе отображение «зуб пилы», для которого было установлено присутствие хаоса. Следовательно, хаос имеет место и в логистическом отображении. Зададим у₀ двоичной дробью в виде случайной последовательности нулей и единиц. То­гда динамика у_n будет хаотической; в терминах двоичного кода она пред­ставляется сдвигом Бернулли. Соответственно, хаотической будет и дина­мика х_n при старте из начальной точки . Интересно, что это хаоти­ческое решение рекуррентного уравнения (*) можно записать в явном виде с помощью формулы

                             

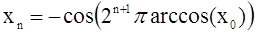
Рассмотрим другой подход к обоснованию хаотической дина­мики ло­гистического отображения при λ = 2. Зададимся вопро­сом: можно ли итери­ровать отображение (*) назад во времени? Выражая с помощью него х_n че­рез х_n+1, получим

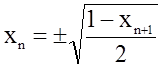
                                            ,                                    (2.7)

т. е., заданному x_n+1 может предшествовать одно из двух зна­чений х_n, отве­чающих разному выбору знака перед квадратным корнем. Обеспечить одно­значность при итерациях в обратном вре­мени можно только указав на каж­дом шаге, какой знак квадрат­ного корня выбрать. Зададим произвольную бесконечную после­довательность из двух символов R и L, например,

                              RLLRLLLRRLLRLRRLL...

и будем на каждом очередном шаге выбирать знак «+», если оче­редной сим­вол R, и «-», если очередной символ L. Соответственно этому, получаемое значение х_n будет располагаться на правом (Right) или на левом (Left) склоне параболы. Заметим, что какой бы ни была RL-последовательность, начав итерации, мы нико­гда не встретимся с появлением под корнем отрицатель­ного чи­сла. Действительно, из из последнего соотношения видно, что неравенство  влечет . Поэтому ничто не мешает взять в качестве RL-кoдa последова­тельность, полученную посредством случайных испытаний. Возьмем теперь точку x, в которую мы по­пали в результате многократных итераций в обрат­ном времени, за начальное условие для уравнения (*). Система будет эво­люцио­нировать хаотически, посещая левый и правый склоны параболы в точном соответствии с символами R и L нашей случайной по­следовательно­сти, читаемой в обратном порядке.

Подчеркнем, что все сказанное справедливо благодаря специ­альному выбору значения параметра λ = 2. Если провести ана­логичные рассуждения для λ < 2, то окажется, что, стартовав от некоторого определенного x, при итерациях в обратном времени можно использовать не все возможные RL-последовательности, a лишь некоторое их подмножество. Причем это под­множество ста­новится все более и более тощим с уменьшением λ. В заключе­ние отметим, что два рассмотренных подхода – по Уламу - фон Нейману и на основе итераций в обратном времени – отвечают разным правилам кодиро­вания траекторий логистического отобра­жения последовательностями двух символов.

 

Двумерные отображения, сохраняющие площадь.

Отображение пекаря.

Построим отображе­ние, отправляясь от рассмотрения динамики типа сдвига Бернулли на множестве последовательностей бесконечных в обе стороны. Запишем такую последо­вательность в виде

                                          (*)

где каждое s_i есть либо 0, либо 1. Обратите внимание на особый разделитель­ный символ – точку с запятой, который встречается в одном-единственном месте; его присутствие позволяет соотносить положение символов с некото­рым «началом отсчета».  

Введем две динамические переменные – действи­тельные числа х и у, при­надлежащие единичному интервалу, определив их через символы s_i следующим образом:

                                  

Пусть трансформация последовательности (*) за один времен­ной шаг со­стоит в том, что все символы сдвигаются на одну по­зицию вправо, так что результатом окажется

                                       .                       

Тогда новые значения x и у будут

                        

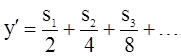
Их можно выразить через старые значения x и у следующим обра­зом:

                                          ,

где фигурные скобки обозначают дробную часть числа, а квадрат­ные – це­лую часть. Другая форма записи тех же соотношений:

                               для     для      

По самому своему построению наша система может демонстри­ровать хаотическую динамику: чтобы получить хаос нужно взять в качестве после­довательности (*) случайный набор символов. Система имеет также бес­конечное множество периодических орбит (циклов) – им отвечают перио­дические последовательности.

В отличие от примеров, приведенных в предыдущем разделе, здесь при­ходим к двумерному отображению, описывающему дина­мику в терминах пе­ременных х и у. Мгновенное состояние на­шей системы определяется зада­нием этих двух величин, причем обе они необходимы для того, чтобы иметь возможность находить последующие состояния по известному начальному.

Можно ли представить себе действие двумерного отображения в на­глядной геометрической форме? Такое представление суще­ствует, и именно оно послужило основанием назвать данную мо­дель отображением пекаря. Рассмотрим единичный квадрат на плоскости (x, у). Разре­заем его пополам, как кусок теста, накладываем одну половинку на другую и раскатываем так, чтобы восстановить исходную форму (см. рисунок).

                       

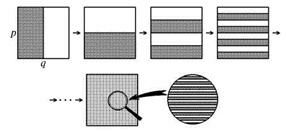
Для наглядности «тесто», оказавшееся слева при пер­вом разрезе, изображено темным, а справа – свет­лым. На ри­сунке показано, как выглядит распределение темного и светлого теста на нескольких последовательных шагах. При большом чи­сле итераций это распределение принимает вид набора тонких и длинных чередующихся темных и светлых полосок. При много­кратном повторении процедуры в конце концов получаем кусок те­ста, который выглядит однородным. Взяв для пробы небольшой кусочек, мы обнаружим в нем присутствующие в рав­ных долях темную и светлую составляющие. Описанное свойство отображе­ния пекаря называется именно так, как мы его и назвали бы на «бытовом»   языке, – перемешивание.

Отображение пекаря является консервативной системой или, используя терминологию, специфическую для двумерных отобра­жений, это отображе­ние, сохраняющее площадь. Если взять некоторую область на плоскости (x, у) и подвергнуть каждую ее точку действию отображения пекаря, то она пе­рейдет в некото­рую другую по форме область, но площадь новой области ос­танется той же самой. Формальное правило для проверки этого свойства со­стоит в том, что должен равняться единице определитель, по­строенный из производных, – якобиан. Для отображения пекаря имеем:

                                                     

В более широком контексте вместо «площадь» говорят «мера». В слу­чае двумерного фазового пространства мера – это площадь, в случае одно­мерного – длина, в случае трехмерного – объем. Мы уже интерпретировали представленную на рисунке динамику как перемешивание слоев двух сортов теста или, если угодно, двух жидкостей – темной и светлой. Сохранение меры отвечает тому, что эти жидкости являются несжимаемыми.

Странные хаотические аттракторы

Рассмотрим примеры, иллюстри­рующие принципиальную возможность хаоса как стационарного ре­жима динамики диссипативных систем. (Имеется в виду стацио­нарность в статистическом смысле, когда постоянны лишь усред­ненные за достаточно большой интер­вал времени статистические характеристики динамики.) Это двумерные и трехмерные модель­ные отображения, в фазовом пространстве которых име­ется притя­гивающее множество сложной структуры, называемое странным хаотическим аттрактором.

Обобщенное отображение пекаря. Модифицируем рассмотренное выше отображение пекаря. Пусть первоначальный разрез «куска те­ста» – единичного квад­рата производится в отношении  к , при этом . Далее оба куска растягиваются по горизонтали до единичной длины, сжимаются по верти­кали, так что их высоты будут соответственно  и , , и располага­ются в преде­лах единичного квадрата у верхнего и нижнего его края.

                                       

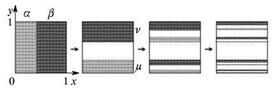
В аналитической форме предлагаемое отображение записывается следующим образом:

          для    для                   

Заметим, что суммарная площадь прямоугольников, образовав­шихся после применения преобразования, уменьшилась на фак­тор , т. е., оно уже не относится к классу сохраня­ющих площадь. Это диссипативная система с двумерным фазо­вым пространством. На рисунке показано, что про­исходит при нескольких последовательных итерациях обобщенного отобра­же­ния пекаря. Образуется характерная система горизонтальных по­лос, сум­марная ширина которых убывает с ростом числа итераций как . Объ­ект, возникающий в пределе бесконечно боль­шого числа итераций, в сечении представляет собой так называе­мое двухмасштабное канторово множество. Процедура его постро­ения состоит в том, что берется единичный отрезок, делится в отношении , и средняя часть исключается. То же са­мое проделывается с двумя оставшимися отрезками, затем с каждым из от­резков, возникших на предыдущем шаге, и т. д. Заметим, что классическое множество Кантора отвечает частному случаю данного построения, а именно, выбору .

Аттрактор имеет нулевую меру, поскольку суммарная площадь полос на n-м шаге дается выражением   и стремится к нулю при , так как .  Все точки исходного единичного квадрата приближаются к ат­трактору. В то же время аттрактор обладает тем свойством, что соседние по горизонтали точки удаля­ются друг от друга при последовательных итера­циях, т. е., имеет место неустойчивость. Отметьте сочетание устойчивости в смы­сле наличия притяжения к аттрактору и неустойчивости в смы­сле разбе­гания точек на аттракторе. Поперечная структура в виде канторова или кан­тороподобного множества очень характерна для странных аттракторов.

Аттрактор Плыкина. Рассмотрим пример двумерного отобра­жения, обладающего свойством непрерывности и имеющего хао­тический аттрактор. Этот пример позволяет уяс­нить важную концепцию гипер­боличности – свойства, наличие которого позволяет строго математически обосновать присутствие хаоса.

Рассмотрим область R на плоскости (x, у), показанную на рисунке. Она состоит из квадрата и трех полудисков с полукруг­лыми вырезами. Об­ласть покрыта штриховкой, показывающей заданное на ней поле направле­ний. Определим двумерное отобра­жение так, чтобы результатом его действия на точки области R была фигура, показанная на рисунке справа. Заметьте, что поле напра­влений, возникающее после применения отображения, совпадает с ис­ходным.

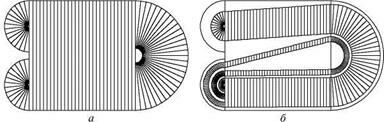На следующем рисунке показано, что получается при многократном дей­ствии опи­санного отображения. Точки, заполнявшие в начальный момент область R, сконцентрирова­лись на аттракторе,  который пред­ставляет собой некоторое сложно и тонко устроенное множество.

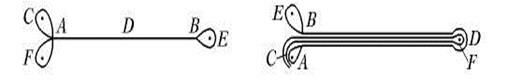Динамика отображения Плыкина проясняется в свете следующего на­блюдения. Рассмотрим точки како­го-либо одного отрезка из числа обра­зующих  штриховку  на предыдущем рисунке. Нетрудно видеть,  что все эти  точки будут демонстрировать одну и ту же динамику в том смысле, что будут одновременно по­сещать каждую из подобластей (квадрат и три полудиска), из которых по­строена область R.  Если отождествить точки, принадлежащие каждому определенному отрезку, то вместо динамики в двумерном фазовом простран­стве можно рассматривать одномерную динамику. Фазо­вым пространством для этой одномерной динамики служит «ре­зиновая нить», имеющая две петли на одном конце и одну петлю на другом (см. рисунок).

 

Представим себе, что эта нить натянута на три гвоздика. Один шаг итераций будет состоять в том, что мы определенным образом растягиваем нить и вновь натягиваем ее на те же гвоздики.

Аттрактор Смейла-Вильямса. Пример хаотического аттрактора, по­лучивший наименование соленоид Смейлa-Вилъямсa, реали­зуется в трех­мерном отображении, которое строится следующим образом. Рассмотрим трехмерную область в форме тора. Представляя его для наглядно­сти как резиновый бублик, растянем его в длину, сложим вдвое и вложим в исходный тор. Чтобы он там поместился, приходится предположить, что в ходе процедуры общий объем «бублика» уменьшается – площадь попереч­ного се­чения должна уменьшиться более чем в два раза.

                         

На следующем рисунке показано, как выглядит поперечное сечение ис­ходного тора после однократного и двукратного применения ото­бражения. Это по­хоже на процедуру построения множества Кан­тора: на каждом шаге в сече­нии имеется некоторое число дис­ков.

                              

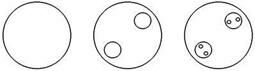
Очередной шаг построения состоит в том, что внутри каждого диска выде­ляются две меньшие области в форме дисков, которые оставляются для сле­дующего шага, а все остальное множество ис­ключается. То, что останется в итоге, и есть сечение аттрактора Смейла-Вильямса.

Имея в виду описанную геометрическую конструкцию, можно предло­жить аналитическую форму отображения. Ее удобно пред­ставить в цилинд­рических координатах , которые связаны с обычными декартовыми координатами (x, у, z) как

                           .                                       (2.22)

Тогда подходящей формой отображения будет

                                (2.23)

где  = 0,2,  = 0,3.  Поверхность исходного тора в параметриче­ской форме задается уравнениями

Люди также интересуются этой лекцией: Эстезиология.

       , ,   ,              (2.24)

Приведенные примеры аттракторов Плыкина и Смейла-Вильямса сконст­руированы так, чтобы они обла­дали свойством, называемым гиперболич­ностью.

Когда говорят, что аттрактор какой-либо динамиче­ской системы гиперболиче­ский, то имеют в виду, что все принадлежа­щие ему траектории гиперболические (седловые), т.е., их ок­рестность устроена так, как показано на рисунке.

                           

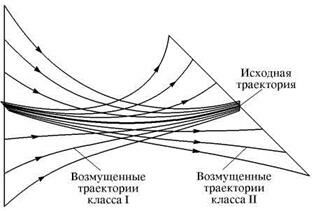
Возь­мем лю­бую траекторию на аттракторе и рассмо­трим все­возможные близкие к ней возмущенные траектории. В линей­ном приближении среди них выделяется класс траекторий (I), которые приближаются к исходной, причем в среднем по экспоненте, и класс тра­ек­торий (II), приближающихся к исходной в обратном времени, тоже в среднем по экспоненте. Поскольку речь идет о рассмотрении дина­мики около исход­ной траектории в линейном приближении, то любой из множества инфините­зимально возмущенных траекторий сопоставляется элемент линейного век­торного пространства (математики называют его касательным пространст­вом), причем все множество исчерпывается всевозможными суперпозициями векторов, ассоциирующихся с упомя­нутыми выше возмущениями класса I и П. Подчеркнем еще раз, что так должна быть устроена окрестность у всех принадлежащих аттрактору траекторий.

Доказано, что системы, обладающие свойством гиперболично­сти, структурно устойчивы, иными словами, это свойство грубое. Если некоторая система имеет гиперболический аттрактор, то это будет справедливо и для систем, полученных произвольным до­статочно малым непрерывным возму­щением исходной системы. Исходя из предположения о гиперболичности ат­трактора, можно строго доказать присутствие всех других свойств, являю­щихся су­щественными атрибутами хаоса.