Теория протекания

ГЛАВА III. Теория  протекания

Решёточные задачи

Термин «протекание» – вольный перевод английского термина percolation (просачивание), впервые употребленного в 1957 г. С. Р. Бродбен­том и Дж. М. Хам­мерсли в связи с новым классом математических задач. Эти задачи естественно возникают при рассмотрении протекания жидкости по случайному лабиринту. Это приложение и дало название всей математиче­ской теории.

Рассмотрим постановку простейших задач теории протекания. Пред­ставим себе бесконечную пространственную или плоскую решетку. Назовем связями отрезки между ближайшими узлами решетки. Пусть по каждой связи в обе стороны может протекать некоторая жидкость, так что каждый смочен­ный узел мгновенно смачивает все соседние узлы. Если в такой решетке смо­чить один узел, то все остальные узлы также оказываются смоченными. Раз­личным образом вводя в условия задачи случайные элементы, можно полу­чить разные задачи теории протекания.

Начнем рассмотрение с задачи связей (bond problem). Предположим, что каждая связь может находиться в двух состояниях. Она может быть разо­рванной (и тогда она не пропускает жидкость) или целой. Пусть вероятность того, что произвольная связь цела, есть х и не зависит от состояния других связей. Тогда мы имеем набор целых и разорванных связей. Концентрация (относительная доля) первых есть х, а концентрация вторых (1 – х). Картина распределения целых и разорванных связей фиксирована и во времени не из­меняется.

Теперь после смачивания одного узла решетки могут возникнуть две разные ситуации: исходный узел может смочить либо конечное, либо беско­нечное число узлов. Какая из этих двух возможностей реализуется, зависит от доли целых связей решетки. Однако в силу случайного расположения це­лых и разорванных связей имеет значение и выбор исходного узла. Для ха­рактеристики системы в целом, удобно гово­рить не об одном конкретном ис­ходном узле, а о вероятности того, что произвольный исход­ный узел смачи­вает бесконеч­ное число узлов. Очень важно, что в бесконечной решетке эта вероятность не зависит от кон­кретной  реализации, т. е., от  того, каким обра­зом легли це­лые и разорванные связи. Для заданной решетки она зависит только от х и обо­значается Р^(b)(х) (индекс b указывает на то, что величина от­носится к задаче связей).

Графики  функций Р^(b)(х),  полученные с помощью численных расчетов, при­ведены для различных решеток на рисунке. Кривые 1, 2, 4 относятся к трехмерным ре­шеткам, а остальные три кривые – к двумерным. При малых х  величина Р^(b)(х) ≡ 0,  так  как  разорванные связи не позволяют жидкости отойти далеко от исход­ного узла. При х, близких к единице, вероятность Р^(b)(х) также близка к единице.

Важнейшее значение имеет вве­денное Бродбентом  и Хаммерсли [1]   понятие порога протекания (критической вероятности). Порогом проте­кания (критической вероятностью) x_с называют верхнюю границу тех значений х, для которых Р^(b)(х) = 0. Общепринятая точка зрения, подтверждаемая чис­ленными расчетами, состоит в том, что за порогом протекания функция  Р^(b)(х) нарастает до единицы, а при (х - х_с) << 1

Рекомендуемые материалы

                                               ^(b)(х) ∞ (х — х_с)^β ,            

где β  — критический индекс, называемый параметром порядка.

Это связано с тем, что поведение Р^(b)(х) с увеличением х напоминает поведение параметра порядка фазового перехода второго рода: при х<х_с про­текания нет, а при х=х_с оно возникает. Существование определенного значе­ния порога протекания х_с, так же как и самой функции Р^(b)(х), возможно лишь на бесконечной решетке, для которой все случайные реализации разорван­ных связей с заданным значением х с точки зрения протекания эквива­лентны.

Наряду с вероятностью соединить бесконечное число узлов Р^(b)(х), можно говорить о вероятности Р_N^(b)(х) того, что данный узел смачивает по крайней мере N узлов, где N — большое, но конечное число. Вероятность Р_N^(b)(х), разумеется, отлична от нуля при всех 0<х<1, хотя при N много боль­ших 1 и х < х_с она очень мала. Вероятность Р^(b)(х) получается из Р_N^(b)(х) пре­дельным переходом к N = ∞:

                                                                        

                                                                                                                                          

Примером задачи связей может быть такая. Пусть проектируется фрук­товый сад, представляющий собой квадратную решетку, в узлах которой рас­тут деревья. Известно, что заболевшее дерево заражает другое дерево, нахо­дящееся от него на расстоянии r, с вероятностью f(r), где f(r) — очень быстро убывающая функция. Требуется найти минимальный период решетки, при котором одно заболевшее дерево способно заразить лишь конечное число де­ревьев, т.е., отсутствует опасность эпидемии. Из условия задачи очевидно, что контактами отдалённых соседей можно пренебречь, а доля контактов между ближайшими деревьями, приводящих к заражению, равна f(h), где h —период решетки. Если таким контактам сопоставить целые связи решетки, а остальным — разорванные, то получим задачу связей, причем х = f(h). По­этому искомый минимальный период h_min определяется равенством

f (h_min) = x_c                       

Вторая основная задача теории протекания – задаче узлов (site problem). В этой задаче все связи считаются целыми, а «портятся» узлы: их называют перекрытыми или открытыми. Перекрытые узлы не пропускают жидкость, ни в какую сторону. Они не могут быть смочены и не смачивают другие узлы. Обозначим через х долю открытых узлов и через P^(s) (х) – ве­роятность того, что произвольный узел смачивает бесконечное число узлов (индекс s означает, что соответствующая величина относится к задаче узлов). Как и в задаче связей, существует порог протекания x_c(s) – верхняя граница значений х, для которых P^(s) (х) = 0.

Задачи узлов и связей удобно сформулировать, введя понятие класте­ров и не используя представление о растекании жидкости. Пусть случайным образом долю х узлов решетки выкрасили в черный цвет, а оставшиеся узлы — в белый. Будем называть связанными любые два черных узла, являющиеся ближайшими соседями. Назовем кластером совокупность черных узлов, свя­занных друг с другом как непосредственно, так и посредством цепочек свя­занных черных узлов. На языке кластеров динамика возникновения протека­ния при увеличении х выглядит следующим образом. При малых х все кла­стеры невелики. Однако по мере приближения к порогу протекания отдель­ные кластеры сливаются и средний размер кластеров возрастает. В точке х = х_с впервые возникает черный бесконечный кластер. Он напоминает собой случайную сетку и пронизывает все пространство. В «порах» бесконечного кластера размещаются конечные изолированные кластеры (см. рисунок).

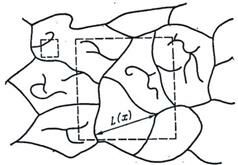
Понятие бесконечного кластера позволяет дать иную трактовку веро­ятности P^(s)(х). Так как только узлы бесконечного кластера смачивают беско­нечное число узлов, вероятность P^(s)(х) равна отношению числа узлов, при­надлежащих бесконечному кластеру, к полному числу узлов решетки. Дру­гими словами, P^(s)(х) есть   плотность   бесконечного   кластера.   Возрастание P^(s)(х) при удалении от порога протекания в сторону больших х означает, что бесконечный кластер, постепенно присоединяя конечные кластеры, из очень редкого, «бестелесного» становится все более плотным. Средний размер его «пор» постепенно убывает. Соответственно убывает среднее число частиц тех конечных кластеров, которые остаются изолированными.

В задаче связей таким же образом можно говорить о конечных и беско­нечных кластерах из целых связей и связанных ими узлов: плотностью бес­конечного кластера связей P^(b)(х) называют отношение числа его связей к полному числу связей решетки.

Считается, хотя и не является строго доказанным, что в системе не мо­жет существовать несколько бесконечных черных кластеров, не связанных друг с другом. Предположим противное, т.е., допустим, что в некоторой об­ласти значений х_с<х<х₁ существуют два бесконечных кластера, пронизы­вающих все пространство. Возьмем значение х=х_с+∆/2, где ∆<x₁—х_с. Соот­ветствующие этому х два бесконечных кластера обладают конечной плотно­стью и везде находятся на конечном расстоянии друг от друга. Увеличим х до значения х_с+∆, вводя дополнительные черные узлы. Вероятность заполне­ния этими узлами любой фиксированной перемычки между двумя бесконеч­ными кластерами окажется малой, но конечной. В то же время число воз­можных перемычек между бесконечными кластерами бесконечно. Поэтому с достоверностью при х = х_с+∆ оба кластера окажутся связанными в один, что противоречит исходному предположению, поскольку х_с+∆< х₁.

Используя язык статистики кластеров, дадим теперь формальные опре­деления Р(х) и других величин теории протекания на примере задачи узлов. Пусть n_s — число кластеров из s узлов в бесконечной решетке, приходящееся на один узел решетки. Тогда сумма  есть доля узлов решётки, принад­лежащих конечным кластерам. Поскольку доля всех чёрных узлов есть х, доля узлов решётки принадлежащих бесконечному кластеру Р(х) равна

Р(х) = х –

Другой важной величиной теории протекания является среднее число узлов конечного кластера

,

где суммирование происходит по всем конечным s. Согласно численным расчетам, при х→х_с+ 0  или  х→х_с– 0  величина S(x) обращается в беско­неч­ность:

                                      S(x) ∞ | x - x_c |^-γ         ( | x - x_c | << 1)       

   где γ – критический индекс теории протекания.

Обащение в бесконечность S(x) при |х — х_с| → 0 не означает ни того, что больших кластеров больше, чем маленьких, ни того, что боль­шим кластерам при­надлежит подавляющее число черных узлов. Действи­тельно, , следовательно,  простое среднее  остается конечным при x= х_с. Таким образом, основ­ная часть черных узлов и при  х = х_с находится в кластерах с s ~ 1.

Согласно численным расчетам, при |х — х_с| << 1 ве­личина n_s как функ­ция s ведет себя следующим обра­зом. Существует некоторое критическое значение числа узлов в кластере s_c, которое растет при х→х_с+0 и х→х_с–0:

S_с∞ | x - x_c | ^{– ∆},         ∆ >0

При s << s_c величина n_s убывает с ростом s по слабому степенному закону, а при s>>s_c –  по более резкому экспоненциальному закону. Обращение в бесконечность величи­ны S(x) при х→х_с является отражением роста числа узлов в критических кластерах, т.е., удаления границы экспонен­циального спада n_s.

Третьей важной характеристикой теории протекания является корреля­ционная функция. Чтобы ввести ее, определим функцию g(r_i,r_j), положив ее равной едини­це, если узлы i и j черные и принадлежат одному конеч­ному кластеру, и равной нулю во всех остальных слу­чаях. После этого введем пар­ную корреляционную функ­цию, усреднив g(r_i,r_j) по всем узлам решетки:

G (r,x) = G( r_i  – r_j, x) ≡ <g ( r_i, r_j )>

При r → ∞ функция G(r, x) стремится к нулю, так как число кластеров n_s размера s убывает с ростом s. На расстояниях r, меньших среднего размера критиче­ских кластеров, который мы обозначим L(x), опреде­ляющую роль в создании корреляции играют кластеры с s<<s_c(x). Следовательно, в этой об­ласти значений r функция G(r, x) убывает степенным образом с ростом r. При r>>L(x) главную роль играют экспоненциально редкие кластеры с s >> s_c(x), и поэтому G(r, x) убывает экспоненциально с ростом r.

Естественно считать, что средний размер критическо­го кластера L(x) является единственной характерной длиной функции G(r, x), и назвать эту длину радиусом корреляции. Поскольку число узлов критического клас­тера при x→x_c ± 0 стремится к бесконечности, радиус корреляции L должен воз­растать при приближении к по­рогу протекания

                                L (x) ≈ | x - x_c|^-ν           ( | x - x_c|<<1),         

где v — критический индекс длины корреляции. Обыч­но считают, что кри­тические индексы γ, ∆, v одинаковы при х>х_с и х<х_с. При х > х_с малая вероят­ность воз­никновения конечных кластеров с размером больше L(x) означает одновременно малую вероятность пор бесконеч­ного кластера такого размера. Поэтому при х > х_с  длину корреляции можно интерпретировать как характерный размер пор сетки бесконечного класте­ра. Можно сказать, что длина корреляции дает пред­ставление о среднем расстоянии между уз­лами сетки, или о ее «периоде». 

Для справки приведены значения порогов протекания задач связей и узлов для трёх типов решёток: 

треугольная             x_c(b) = 0,3473    x_c(s) = 0,500 

квадратная               x_c(b) = 0,5000    x_c(s) = 0,590 ± 0,01

шестиугольная        x_c(b) = 0,6527     x_c(s) = 0,700 ± 0,01

М. Ф. Сайке и Дж. У. Эссам, изучая методом рядов поведе­ние S(x) вблизи х = х_с, впервые вычислили критический индекс γ для задачи узлов и связей. Оказалось, что на всех исследованных ими плоских решетках – квад­ратной, треугольной и шестиугольной – значения γ близки. Аналогичное совпадение было зафиксировано в трехмерном случае для простой, объемно-центрированной и гранецентрированной кубических решеток и решетки ал­маза. Основываясь на этих данных, они предположили, что индекс γ универ­сален, т.е., для фиксированной размерности пространства он не зависит ни от характера задачи, ни от вида решетки Имеющиеся теперь данные не проти­воречат гипотезе о том, что все индексы теории протекания универсальны.

Другим основным методом численного решения за­дач теории протека­ния является метод случайных испы­таний, или метод Монте-Карло.

Величина х_с сильно зависит от ре­шетки и характера задачи. Для задачи связей сущест­вует приближенное эмпирическое правило, по которому х_с(b) выражается через простые характери­стики решеток – размерность d и число ближайших со­седей Z:

    , 

где B = Zx—среднее число узлов, связанных с данным узлом решетки. Это соотношение выполняется с точностью до нескольких процентов при изме­нении вели­чин Z и х_с(b) в 3 раза. Для задачи узлов величина Zx_c не является даже приближенным инвариантом. Однако в этом случае су­ществует другой приближенный инвариант, замеченный  Г. Шером и Р. Залленом.

Построим вокруг каждого узла решетки окружность (сферу) с радиу­сом,  равным  половине расстояния до ближайшего соседа (см. рисунок). Пусть f есть доля пло­щади (объема), попадающая внутрь этих окружностей (сфер). Величину f называют плотностью упаковки. Ее легко вычислить для каждой решетки. Г. Шер и Р. Заллен подсчитали долю площади (объема), ко­торая при х=х_с находится внутри окружностей (сфер), построенных во­круг черных узлов. Для этого надо вычислить произве­дение υ_c = fx_c(s). Оно оказы­вается приблизительно оди­наковым для всех решеток одной размерности:

υ_c = 0,15±0,01 при d = 3  и  υ_c = 0,4±0,02 при d = 2.

Ис­следование решеточных задач началось раньше других, и именно на них отработаны методы и проверены основные идеи теории протекания. Кроме них существуют еще два больших клас­са задач теории протекания: континуальные задачи и за­дачи на случайных узлах.

Континуальные задачи

Континуальные задачи формулируются сле­дующим образом: допустим, что во всем про­странстве задана случайная непрерывная функция V(r), не нарушая общно­сти, будем считать, что сред­нее значение <V(r)> = 0. Зададим веществен­ное число V и  мысленно «покра­сим» чер­ной краской области пространства, где V(r) < V, а ос­тальные области – белой.

При изменении V от - ∞ до + ∞, объем чер­ных об­ластей меняется от нуля до объема всего пространства (см. рисунок). Изолированные вна­чале

                    

                                         

черные «озера» сли­ваются друг с другом и при больших V образуют «океан». Требуется найти нижнюю границу V_c тех значений V, для которых имеется возможность, стартуя из некото­рых черных точек, уходить на бесконечное рас­стояние, двигаясь только по черным областям. Величина V_c называется в этом случае уров­нем протека­ния.

Можно сформулировать задачу и на языке, аналогичном кластерному. Возникновение протекания соответствует на этом языке образованию связ­ной черной области, обладающей бесконечным объемом. Естественно, обоб­щается и формулировка о протекании через конечный объем – здесь нужно говорить о возник­новении путей протекания «по черному» между проти­во­положными сторонами квадрата (гранями куба).

Континуальная задача близка к сформулированным выше решеточным задачам. Пусть есть решетка со столь малым периодом, что функция V(r) практически на нем не меняется. Зафиксируем V и будем считать, что узлы ре­шетки, находящиеся в черных областях, – черные, а в белых – белые. При увели­чении V увеличивается доля черных узлов

    

где υ(V) — доля простран­ства, в которой V(r)<V, a F(V)—функция распреде­ле­ния потенциала V. Уровень протекания V_c, таким обра­зом, может быть найден из того условия, что доля про­странства, занятого черными областями на пороге проте­кания:

   

равна порогу протекания х_с для задачи узлов, отличаю­щейся от сформулиро­ванной ранее тем, что распределе­ние черных и белых узлов коррелированно в соответ­ствии с видом V(r), т. е., черные и белые узлы сгруппированы в кла­стеры.

Наряду с протеканием по черному можно говорить и о протекании по белому. При малых V белое заполняет почти все пространство, образуя «кон­тинент», окружаю­щий своими «берегами» черные «озера». При больших V «континент» разбивается на изолированные «острова» и протекания по бе­лому нет. Назовем уровнем протекания по белому значение V = V`<sub>c</sub>, при ко­тором протека­ние по белому исчезает. Если говорить o случайных по­тенциа­лах V(r), обладающих конечным радиусом корре­ляции, то в двумерном слу­чае существует простая связь между V<sub>c</sub> и V`_c

Действительно, рассмотрим протекание по черному и по белому между противоположными сторонами квадрата с размерами, много большими ра­диуса корреляции потенциала. В этом случае ясно, что отсутствие протека­ния по черному слева направо означает существование протекания по белому сверху вниз. С другой стороны, если имеется протекание по белому, напри­мер, слева направо, то протекание по черному сверху вниз отсутствует.

Поскольку в очень больших квадратах протекание по одному из цветов в обоих направлениях возникает при одинаковом значении V, то в предыду­щих двух фразах можно опустить слова «слева направо» и «сверху вниз», и приходим к следующему заключению. Протекание по черному исчезает при том же значении V, при кото­ром возникает протекание по белому, т. е., V_c = V`_c .

Теперь можно определить V_c для потенциала, статистические свойства  которого симметричны относительно значения V = 0. Для таких потенциалов очевидно, что V_c = - V`<sub>c</sub>   и с учетом V<sub>c</sub> = V`_c= 0  и  θ_с =0,5 , т.е., на пороге про­текания площадь поровну распределена между белым и черным цветом.

Для трехмерного потенциала, как и для двумерного, не может отсутст­вовать протекание по обоим цветам. Здесь, однако, протекания по черному и по белому могут сосуществовать, так как каналы, по которым осуществля­ется протекание по белому и по черному, не обязаны пересекаться. Поэтому в трехмерном случае имеет место лишь неравенствоV_c ≤ - V`_{c  ,} т.е., с точки зрения протекания возможны три различные области значений V:

1) V<V_с – есть протекание по белому, но нет по черному;

2) V_c≤V<V`_c — есть протекание и по белому, и по черному;

3)V≥V_c — есть протекание по черному, но нет по белому.

Для статистически симметричного потенциала выполняется

  и     .

Задачи на случайных узлах

Рассмотрим задачи протека­ния по случайным узлам – это точкам, хао­тически распределенным в пространстве.

Пусть среднее чис­ло узлов в единице объема задано и равно N. И пусть также ξ_ij – некоторая функция вектора r_ij, соединяющего два узла i и j. Зада­дим некоторое число ξ и будем считать, что узлы i и j связаны, если выпол­нено неравенство ξ_ij  ≤ ξ, которое в дальнейшем называется условием связно­сти.

Если два узла связаны непосредственно или с помощью попарно свя­занных узлов, то они принадлежат одному кластеру. Требуется найти порог протекания ξ_c, т.е., нижнюю границу, значений параметра ξ, для которых су­ществует бесконечный кластер.

Простейшей из этого класса является задача с условием связности r_ij ≤ r. Это условие выполняется, если узел j находится внутри сферы радиуса r, описанной вокруг узла i. Поэтому задача имеет следующую геометрическую интерпретацию. Пусть вокруг каждого узла построены сферы одинакового радиуса r. Требуется найти наименьшее значение r = r_с, при котором сущест­вуют бесконечные цепочки узлов, где каждый последующий узел лежит внутри сферы, построенной на предыдущем, а иногда строят сферы с радиу­сом r/2 и определяют значение r, при котором беско­нечный кластер образуют перекрывающиеся сферы (см. рисунок).

                                

Порог протекания, или перколяционный радиус, r_с зависит только от концентрации узлов N и по соображениям размерности пропорционален N^l/3. Часто бывает удобным вместо r_с говорить о пороговом значении безразмер­ного параметра , имеющего смысл среднего числа связей на один узел. Анало­гичную двумерную задачу называют задачей окружностей. В этом случае удобно пользоваться величиной ,

где  – число случайных узлов на единицу площади, а  – двумерный перко­ляционный радиус.

В пределе очень большого r_вз, когда в сферу взаимодействия попадает очень много узлов решетки и дискретность положения частиц больше несу­щественна, возникает задача сфер, с той только разницей, что значение r_вз  теперь задано, а ищется концентрация частиц (случайных узлов). Если обо­значить через Z число узлов решетки, попадающих в сферу взаимодействия, то Zx есть среднее число черных узлов, связанных с данным узлом, и, оче­видно, для всех решеток одной размерности .

В задачах на случайных узлах можно ввести крити­ческие величины, аналогичные параметрам решеточных задач узлов. Пусть n_s — число класте­ров из s узлов в некотором объеме, отнесенное к полному числу узлов объ­ема. Тогда

            

Вблизи порога В_с

Ещё посмотрите лекцию "31 Организация и планирования расследования" по этой теме.

P(B) ∞ (B - B_c)^β,    S (B) ∞ | B - B_c | ^-γ      

По аналогии с решеточными задачами можно ввести корреляционную функцию и радиус корреляции L. Вбли­зи порога

L (B) ≈  N ^-1/3 | B - B_c |^-υ  ,    

где среднее расстояние между узлами N^-1/3 фигурирует в качестве естествен­ного масштаба длины. Радиус кор­реляции имеет смысл характерного разме­ра критических кластеров, т.е., самых больших из тех кластеров, для которых величины n_s еще не экспонен­циально малы. Две последние формулы можно записать, введя вместо разности В — В_с безразмерную перемен­ную (r — r_с) / r_с или, в более общем случае, (ξ — ξ _с) / ξ_с . Например,

 ,      или         

Поскольку критические индексы не зависят от геометрии решетки, ес­тественно считать, что они не изменяются и при переходе от решеток к слу­чайному расположению узлов.