1. Цифровые и дискретные сигналы

Системы цифровой обработки сигналов непосредственно оперируют с последовательностями цифровых кодов (чисел), которые называют цифровыми сигналами. Цифровой сигнал в радиоэлектронных системах образовывается в результате аналого–цифрового преобразования непрерывных (континуальных) сигналов. Аналого-цифровое преобразование (АЦП) включает три этапа: дискретизацию сигнала по времени (пространству), квантование по уровню и цифровое кодирование.

На первом этапе образуется дискретный сигнал x[D], который является функцией дискретной переменной D, принимающей только фиксированные значения. Если эти значения являются равноотстоящими D=nT_¶, (T_¶=const), то выбрав соответствующий масштаб, их можно приравнять натуральным числам. В этом случае дискретный сигнал определяют функцией номера отсчета (выборки) x[n]. Говорят, что T_¶=1/f_¶  это период дискретизации, f_¶  - частота дискретизации, а n- номер отсчета.

Второй этап АЦП дает дискретный квантованный сигнал x_кв[nT_¶], отличающийся конечным множеством принимаемых им значений. На третьем этапе получается цифровой сигнал x_ц[nT_¶] в виде последовательности цифровых кодов с заданным числом разрядов.

Вычислительные средства в соответствии с заданным алгоритмов цифровой обработки F преобразуют сигнал x_ц[nT_¶] в выходной цифровой сигнал y_ц[nT_¶] = F{x_ц[nT_¶]}. В цифровых системах с аналоговым выходом цифровая форма выходного сигнала y_ц[nT_¶] преобразуется в аналоговую y(t) с помощью цифро-аналогового преобразования.

1.1. Дискретизация сигналов и теорема отсчетов

Наиболее удобным с точки зрения организации обработки и естественным способом дискретизации является представление сигналов в виде выборок их значений (отсчетов) в отдельных, регулярно расположенных точках T_¶ = . Практически операция дискретизации осуществляется путем измерения значений сигнала с помощью датчика, действие которого можно описать как свертку с некоторым ядром :

                                            (1)

Набор значений  составляет дискретное представление сигнала. Ядро  называется апертурой дискретизации. Восстановление непрерывного сигнала из приближенных значений  выполняется путем интерполяции

Рекомендуемые материалы

                                              (2)

с помощью интерполирующей функции , которая называется апертурой восстановления.

Если исходить только из точности аппроксимации, то существует важный класс сигналов и соответствующие ему базисные функции, для которых распределения (1) и (2) являются абсолютно точными. Это сигналы, спектр Фурье которых U(f)=F{u(t)} отличен от нуля только в пределах ограниченного участка области определения (сигналы с ограниченным спектром).

Пусть сектор сигналов отличен от нуля на интервале , т.е.

.                                                   (3)

где                            .

Для таких сигналов базисы дискретизации и восстановления образуются из функций отсчетов:

;      ,                      (4)

а (1) и (2) переходят в точные равенства:

                                     (5)

.                                           (6)

Эти соотношения называются теоремой отсчетов. Равенство (5) означает, что отсчетами сигнала являются его значения в точках , полученные после пропускания сигнала через инвариантный к сдвигу «идеальный» фильтр с импульсной и частотной характеристиками:

,                                    (7)

.                                                      (8)

         Равенство (6) означает, что процедуру восстановления непрерывного сигнала  из его отсчетов  можно представить как пропускание через идеальный фильтр нижних частот (7), (8) непрерывного сигнала вида

,                                             (9)

спектр которого  представляет собой периодически продолженный с периодом  спектр  сигнала :

.                                                  (10)

Действительно, при такой фильтрации спектр  умножается на частотную характеристику фильтра (8), выделяющую только один период спектра, соответствующий  и равный спектру сигнала . Периодическое продолжение спектра (10)  возможно, если шаг растрирования  меньше или равен величине, обратной протяженности спектра. В противном случае происходит перекрытие (наложение) соседних периодов спектра сигнала

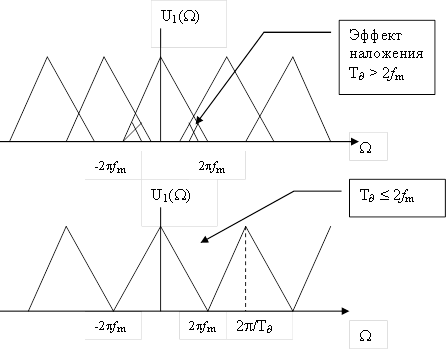, и идеальным фильтром нижних частот уже невозможно выделить спектр сигнала в чистом виде (рис 1).

Рис. 1

В восстановленном сигнале появляются излишние компоненты за счет наложения слева и справа на основной (нулевой) период спектра фрагментов спектра плюс первого, минус первого и следующих порядков. При этом, если в исходном сигнале они имели частоту, скажем, , то в восстановленном сигнале их частота оказывается равной , то есть более низкой. Это влияние снижения частоты периодических составляющих в сигнале при дискретизации с шагом, не соответствующей максимальной частоте сигнала, называется эффектом наложения. Для того чтобы этих искажений не было, очевидно, необходимо перед растрированием с шагом  пропустить сигнал через идеальный фильтр нижних частот (антиэлайсинговый) с полосой пропускания . Сходные по своей природе искажения возникают, если восстанавливающий фильтр имеет полосу пропускания шире, чем .

Теорема отсчетов может быть обобщена на сигналы, содержащие несущую частоту f₀. Это сигналы, спектр которых отличен от нуля на ограниченных интервалах, смещенных относительно нулевой частоты. Дискретизацию сигналов с несущей частотой можно выполнить несколькими способами.

1. Дискретизация с использованием аналитического сигнала. Вместо действительного сигнала u(t) можно рассмотреть аналитический сигнал , где  - преобразование Гильберта u(t). Аналитический сигнал имеет односторонний спектр и к нему теорема отсчетов применима уже в своем обычном виде:

,                               (11)

где  - отсчеты аналитического сигнала,

,

f_l = (f₀ – F) и f_h = (f₀  + F)  – границы частотного интервала в положительной части спектра.

Сигнал на несущей частоте описывается отсчетами своей огибающей и фазы следующим образом:

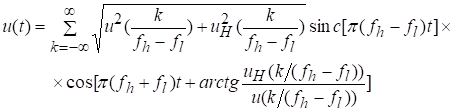
Количество отсчетов определяется только шириной  полосы частот сигнала 2F.

Вещественный узкополосный процесс u(t) может быть представлен посредством ряда с периодически повторяющимися отсчетами после непосредственного выделения вещественной части (11)

.

Заметим, что в том и в другом случае при временной периодической дискре­тизации вещественного узкополосного процесса нужно иметь отсчеты не только самого процесса u(t), но также отсчеты квадратурно сопряженного процесса u_H(t).

2. Другой способ дискретизации состоит в следующем. Попытаемся представить вещественный узкополосный сигнал в виде ряда, коэффициентами которого являются отсчеты самого процесса. Спектр вещественного сигнала с несущей частотой занимает две спектральные полосы. Поэтому при дискретизации такого сигнала с интервалом дискретности, равным величине, обратной ширине спектра периодическое повторение полосы  всегда наложится на полосу  и наоборот. В результате спектр  дискретного, решетчатого процесса не будет совпадать со спектром исходного процесса.

Эта трудность может быть преодолена путем увеличения частоты дискретизации, что приведет к увеличению периода повторения 1/T_¶>2F в спектральной области. Интервал дискретности T_¶ выберем таким образом, чтобы при периодическом повторении спектра U(f) полоса  при любом целом m не накладывалась на полосу .Примем , где b-коэффициент, величину которого нужно определить. Требование неперекрытия полос приводит к неравенству

.

Целое число m выбираем из условия минимизации b с учетом ограничения b³0. Это дает , где - целая часть числа a. Если (f₀/2F)-1/2 – целое число, то b=0 и T_¶=1/4F. Во всех остальных случаях b>0 и период временной дискретизации несколько меньше величины 1/4F.

1.2. Представление дискретных сигналов с помощью функциональных рядов

В системах обработки сигналы задаются на определенном интервале изменения переменной. Для дискретного сигнала – это счетное множество точек, например [0, N-1] или [0, ¥]. В первом случае говорят, что дискретные сигналы определены на конечном интервале [0, N-1], включающем в себя N точек.

Дискретное представление можно рассматривать как аппроксимации аналоговых сигналов с помощью рядов. При этом происходит замена непрерывных значений коэффициентами ряда. Дискретные сигналы представляются в виде линейной комбинации базисных функций. Процесс представления заключается в проектировании сигнала на заданный базис. Коэффициенты представления находятся как скалярные произведения сигнала на соответствующие базисные функции:

                                                                   (12)

Размерность базиса (количество коэффициентов ) ограничивают, основываясь на требуемой точности аппроксимации сигналов , конечной суммой

                                                 (13)

Оптимальные базисы дискретного представления сигналов.

Естественно считать оптимальным такой способ дискретизации, при котором размерность базиса минимальна при заданной точности восстановления сигнала.

Пусть  - сигнал, удовлетворяющий следующим условиям:

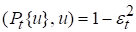
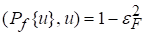
,                                                         (14)

где  – оператор стробирования, выделяющий из сигнала участок протяженностью ;  – идеальный полосовой фильтр, пропускающий только частоты спектра в интервале ;  – ошибки такого усечения по протяжённости и по спектру.

Тогда наилучшим является представление сигнала по функциям, являющимися решением уравнения

,                                (15)

и называемым сфероидальными волновыми функциями (СВФ), причём

,                                (16)

если – наименьшее целое число, превышающее  [3]. При – сфероидальные волновые функции приближаются к отсчётным функциям , и разложение по ним переходит в разложение по теореме отсчётов. При конечном представление (13) по СВФ сигналов, заданных (14), лучше их разложения по отсчётным функциям при том же .

         При статистическом описании сигналов оптимальный – мерный базис для представления отдельных реализаций сигналов обычно определяют как базис, при котором норма ошибки, усреднённая по ансамблю реализаций, минимальна. В этом случае получается результат, известный как теорема Карунена – Лоэва [3]. Минимальное значение нормы ошибки при представлении сигналов на интервале протяженностью достигается при использовании в качестве базиса собственных функций, составляющих  наибольших собственных значений оператора l_k, ядром которого является корреляционная функция сигналов :

.                                   (17)

Минимальное значение нормы ошибки при этом равно

.                            (18)

Такое представление называется разложением Карунена – Лоэва. Коэффициенты разложения Карунена – Лоэва являются некоррелированными (ввиду ортогональности ) случайными величинами).

Для стационарных процессов, когда корреляционная функция зависит только от разности аргументов , при  (становится достаточно большим по сравнения с протяжённостью ) собственные функции  приближаются к комплексным дискретным экспоненциальным функциям с частотами .

В случае бесконечного интервала определения дискретные сигналы представляются с помощью дискретного преобразования Лапласа (ДПЛ)

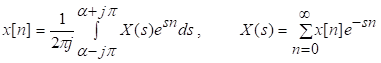
Здесь изображение X(s) есть периодическая функция непрерывной комплексной переменной s=a + jw.. Для удобства ДПЛ часто используют в несколько модифицированном виде, носящим название Z преобразование и получающее путем введения новой переменной z=exp(s).

Z- преобразование дискретной последовательности  имеет вид

    ,

интегрирование осуществляется в области сходимости функции.

В частотно временной области сигнал x[n] может быть описан с помощью дискретного во времени преобразования Фурье

, .

Дискретное во времени преобразование Фурье связано с преобразованием Фурье непрерывного сигнала  соотношением

.

В случае конечного интервала определения, для периодического дискретного сигнала, повторяющегося с периодом NT_¶, x[n] = x[n+lN], удобно использовать базис ортогональных дискретно экспоненциальных функций (ДЭФ). Такое представление называется дискретным преобразованием Фурье (ДПФ) и имеет вид

.

Здесь сигнал x[n] и его спектр X(k) являются дискретными функциями, определенными на конечном интервале N.

Для анализа нестационарных, всплесковых, сигналов часто используют представление с помощью вейвлетных функций в виде коротких, солитоноподобных колебаний  Понятие частоты классического спектрального анализа при этом заменяется масштабом a, а чтобы перекрыть всю временную ось вводится сдвиг функции во времени b.

1.3. Цифровые сигналы

Операция квантования непрерывной величины состоит в том, что континуум ее возможных значений заменяется счетным числом значений. Существующие устройства квантования обычно осуществляют равномерное квантование сигналов, при котором границы интервалов квантования размещаются равномерно в заданном диапазоне значений сигнала, а представители уровней квантования располагаются посередине между этими границами. В случае равномерной процедуры количество порогов квантования оценивается величиной

,

где  и  - максимальная и минимальная амплитуды дискретизируемого сигнала. Пороги квантования разбивают интервал  на (r + 1) интервалов – уровней квантования.

Отсчет непрерывного процесса в АЦП преобразуется в двоичный код из m разрядов, каждый из которых представлен нулем или единицей. Число разрядов определяется числом уровней квантования

.

При когерентной обработке, когда требуется осуществлять цифровую фильтрацию сигналов, когерентную компенсацию помех, число уровней квантования нужно увеличивать, чтобы уменьшить по возможности искажения (из-за квантования) сигналов и помех. На практике часто выбирают , где - дисперсия собственного шума приемника. При этом, число порогов квантования равно , где - динамический диапазон аналоговой части приемника. Отсюда получаем требуемое число разрядов кода  и соответственно число разрядов АЦП:

.

Системы счисления в системах цифровой обработки сигналов. Цифровая система обработки является конечной машиной, работающая с конечным множеством чисел. Невозможно использовать это множество для выполнения арифметических операций в поле вещественных чисел (R, +, ´), поскольку R  - бесконечное множество, большинство элементов которого непредставимо в вычислительной машине.

На практике в процессе обработки осуществляют аппроксимацию арифметики в поле (R,+,´). Часто для такой аппроксимации используется множество F так называемых чисел с плавающей точкой (или машинных чисел). Множество F является частью множества вещественных чисел со следующими свойствами.

1. F – конечное подмножество множества рациональных чисел Q .

2. Элементы F распределены неравномерно на вещественной прямой. Интервал между двумя “соседними” машинными числами очень мал вблизи нуля, а при удалении от него постепенно увеличивается. Интервал между максимально возможным машинным числом и соседним с ним очень велик.

3. Система (F, +, ´) не будет полем (главным образом из-за того, что нет замкнутости относительно обеих указанных бинарных операций.

Практичный выход из возникающих трудностей состоит в представлении вещественного числа x ближайшим к нему машинным числом ; тем самым вводя ошибку округления . Из-за отсутствия замкнутости ошибки округления возникают также в результате арифметических операций над элементами F. Например, если  и  - два соседних элемента F , то число  уже не принадлежит F. Его следует заменить на  - элемент в F, ближайший к z. В этом примере  совпадает либо с , либо с .

Представление целых чисел в системе счисления по смешанным основаниям.

Рассмотрим упорядоченный набор из n целых чисел

,

компоненты которого r₁, r₂,…,r_n называются основаниями. Пусть N есть произведение оснований, т.е. . Известно, что каждое целое число s, такое, что  можно представить в виде

,

где d₀, d₁,…,d_n-1 являются цифрами стандартного представления для смешанного основания и удовлетворяют неравенствам  i = 0,1,…, n-1. Упорядоченный набор цифр d₀, d₁,…,d_n-1 для данного s записывается в виде кода . Например, если r = [2, 3, 5], то N = 30, Следовательно, число 29 можно записать в виде 29 = 1+2(2)+4(2×3) и представление числа по смешанному основанию r имеет вид (29)_r =(1, 2, 4).

В лекции "2.16 Архитектура русского барокко" также много полезной информации.

Стандартной системой счисления со смешанным основанием r называется множество всевозможных наборов цифр типа для целых чисел sÎ[0, N). В частном случае r₁ = r₂ = … = r_n приходим к известному представлению числа в позиционной системе с фиксированным основанием.

Контрольные вопросы и задачи

1. Определить условие наложения спектров для q₁, q₂ двух сигналов  и , если они дискретизируются с интервалом T_¶ = Dt.

2. Показать, что если в предыдущей задаче положить , где m – целое число, то возникает эффект комплексно-сопряженного наложения.

3. Пояснить, в чем различие между преобразованием Фурье непрерывного сигнала, дискретного во времени преобразованием Фурье и дискретным преобразованием Фурье.

4. Определить код представления числа 25 в системе счисления по смешанному основанию N=60.