Основные определения

3.2. Основные определения

Введем операции преобразования СП.

Определение 3.1. Объединением в СП будем называть такую операцию, в результате выполнения которой вершины ni и nj заменяются одной вершиной n, для которой справедливы следующие соотношения: pre(n) = pre(ni) И pre(nj), post(n) = post(ni)  И  post(n j).

Определение 3.2. Разделением в СП будем называть такую операцию, в результате выполнения которой вершина n заменяется двумя вершинами ni и nj , для которых справедливы следующие соотношения:  pre(ni ) И pre(nj) = pre(n),      post(ni) И  post(nj) = post(n).

При вводе основных понятий и определений структур СП будем использовать терминологию работы [7], в  которой  даются  основы  теории  структур.  Обозначим  через

Lm  = {N1, N2,..., Np } множество СП, которое может быть получено путем объединения вершин СП, состоящей из m элементарных сетей.

Определение 3.3. Под частично упорядоченным множеством СП будем понимать систему C = (Lm, Q), в которой на множестве Lm определено бинарное отношение Q = ІіІ (больше или равно), удовлетворяющее следующим свойствам:

 Для всех N О Lm : N  і  N                      (рефлексивность).

 Если Ni  і  Nj   и Nj  і  Ni  , то Ni  =  Nj        (антисимметричность).

Рекомендуемые материалы

 Если  Ni  і Nj  и Nj   і   Nk , то  Ni  і  Nk     (транзитивность).

Под мощностью ЅLmЅ частично упорядоченного множества Lm будем понимать число его элементов.

Определение 3.4 . Выражение "СП Ni покрывает СП Nj" означает, что Ni  > Nj   и что Ni  > Nk > Nj  не выполняется ни для какого Nk .

Рассмотрим физическую сущность отношения ІіІ для множества СП. Каждому элементу Ni множества Lm поставим в соответствие некоторое число ki , которое определяется суммой вершин СП Ni . Число вершин СП Ni будем обозначать как ЅNiЅ (ki = ЅNiЅ). Тогда СП Ni і Nj , если ЅNiЅ іЅNjЅ. Запись Ni = Nj означает, что СП Ni изоморфна СП Nj . Очевидно, что если Ni =Nj, то ЅNiЅ =ЅNjЅ, однако обратное несправедливо.

Очевидно, что операции объединения и разделения влияют на величину ЅNЅ путем изменения числа вершин в СП N . Отсюда следует:

Утверждение 3.1. СП Ni  покрывает СП Nj тогда и только тогда, когда

 ЅNiЅ -ЅNjЅ = 1 .

То есть, Nj может быть получена из Ni в результате выполнения только одной операции объединения, либо Ni  может быть получена из Nj в результате выполнения только одной операции разделения.

Проверим, удовлетворяет ли наша интерпретация отношения ІіІ свойствам определения 3.3.

1). Если число вершин в СП N обозначить через k , т.е. k = ЅNЅ, то очевидно, что  k  і  k . Следовательно, рефлексивность соблюдается.

2). Пусть задана некоторая СП  N . Рассмотрим СП Ni  и Nj , причем Ni  получена из N в результате объединения двух позиций, а Nj  получена из N путем объединения двух переходов. Следовательно, можно составить следующие соотношения: ЅNiЅ= ЅNЅ- 1, ЅNjЅ =ЅNЅ - 1, ЅNi Ѕ =ЅNj Ѕ .

Отсюда Ni і Nj  и  Nj і Ni  , но Ni  № Ni по условиям построения СП Ni и Nj . Следовательно, свойство антисимметричности не выполняется.

3). Доказательство выполнения свойства транзитивности очевидно.

Математические системы, обладающие отношением, для которого выполняются только свойства 1 и 3 определения 3, а свойство 2 не выполняется, называются квазиупорядоченными [7].

Используя определение 3.3 и утверждение 3.1, можно построить графическое представление любой системы C. Для этого каждому элементу множества Lm поставим в соответствие вершину графа ai . При этом вершины графа расположим таким образом, чтобы вершина, соответствующая СП Ni, располагалась выше вершины, соответствующей СП Nj, если Ni > Nj. Вершины ai и aj соединим направленной дугой от ai к aj, если Ni покрывает Nj. Фигура, полученная таким образом, называется диаграммой.

Наименьшим элементом некоторого  квазиупорядоченного  подмножества СП

Lў М Lm будем называть такой элемент No О Lў, что No Ј Ni  для всех Ni О Lў. Наибольшим элементом подмножества Lў будем называть такой элемент NI О Lў, что

 NI  і  Ni   для всех Ni О Lў .

Утверждение 3.2. Минимальным элементом некоторого квазиупорядоченного подмножества СП Lў М Lm является такой элемент Nmin О Lў, что ни для какого Ni О Lў не имеет места Nmin  і  Ni .

Аналогично максимальным элементом подмножества Lў является такой элемент Nmax, что ни для какого Ni О Lў не имеет места Nmax Ј   Ni.

Доказательство. Представим квазиупорядоченное подмножество Cў диаграммой. Рассмотрим любой самый нижний элемент No  данной диаграммы. Очевидно, что для него справедливо No Ј Ni  для всех Ni О Cў, т.к. это следует из правил построения диаграмм. Следовательно, элемент No является наименьшим.

Предположим, что No  не является минимальным элементом Cў, т.е. существует такой элемент Noў О Cў, для которого справедливо No > Noў. Из полученного неравенства следует: либо No не является наименьшим элементом (что противоречит правилам построения диаграммы), либо элемента Noў  не существует.

Аналогично можно доказать существование максимального элемента.

Под верхней гранью k-го уровня подмножества Lў квазиупорядоченного множества СП Lm будем понимать подмножество СП LI М Lm такое, что ЅNi  ½  = k для всех Ni О LI и k >ЅNj  ½ для всех Nj О Lў. Наименьшая верхняя грань (наим.в.гр.) есть верхняя грань с минимальным уровнем. Под нижней гранью l-го уровня подмножества Lў будем понимать подмножество СП Lo М Lm такое, что ЅNiЅ = l для всех Ni О Lo и

l <ЅNjЅ для всех Nj О Lў. Наибольшая нижняя грань (наиб.н.гр.) есть нижняя грань с максимальным уровнем.

Определение 3.5. Структура СП  есть  квазиупорядоченное  подмножество СП

Lў Н Lm , любой элемент которого, удовлетворяющий условию NI > Ni > No , имеет наим.в.гр., содержащую элементы, полученные в результате выполнения одной операции разделения, и наиб.н.гр., которая содержит элементы, полученные в результате выполнения одной операции объединения.

Если Lў = Lm , то структура называется полной.

Теорема 3.1. Полная структура СП обладает только одним наибольшим и только одним наименьшим элементами.

Доказательство. Предположим, что полная структура СП обладает несколькими наибольшими элементами NI1, NI2,..., NIq. Рассмотрим элемент NI1. Из определения наибольшего элемента следует, что NI1 > Ni для всех Ni О Lm ; кроме того, не существует такого элемента Nў, чтобы |N’|>|NI1|. Из этого можно заключить, что NI1 является максимальным. Так как мы рассматриваем полную структуру, то она включает СП, состоящую из элементарных сетей. Обозначим эту СП через NPR. Особенностью данной СП является то, что над ее вершинами невозможно выполнить ни одной операции разделения, т.к. все вершины данной сети являются простыми. Отсюда NPR не имеет ни одной покрывающей СП, т.е. NPR также является максимальной. Однако для заданного числа переходов примитивную систему можно построить единственным образом. Следовательно, NPR эквивалентна NI1.

Аналогичные рассуждения можно привести для всех NIi , где 1 Ј i Ј q. Следовательно, полная структура СП имеет единственный наибольший элемент, который является максимальным и представляет собой примитивную систему NPR . Предположим, что полная структура СП обладает несколькими наименьшими элементами NO1, NO2,..., NOs . Рассмотрим элемент NO1. Из определения наименьшего элемента следует, что NO1 Ј Ni для Ni О Lm ; кроме того, не существует такого элемента Nўў,  чтобы ЅNўўЅ <ЅNO1Ѕ. Из этого можно сделать вывод, что NO1 является минимальным элементом. Рассмотрим элемент NO, который включает только две вершины (переход и позицию), связанные друг с другом циклически. Так как мы рассматриваем полную структуру СП, то данный элемент принадлежит множеству Lm . Особенностью данной СП является то, что в ней нельзя выполнить ни одной операции объединения. Следовательно, данный элемент не является покрывающим ни для какого другого элемента. Отсюда NO является минимальным элементом полной структуры СП.

Очевидным является тот факт, что для двух вершин (позиция и переход) без учета кратности дуг можно построить только одну СП, которая описывается следующими соотношениями: pre(p) = post(p) = {t}, pre(t) = post(t) = {p} . Следовательно, элемент NO эквивалентен элементу NO1. Аналогичные рассуждения можно привести для всех элементов NOi . Следовательно, полная структура обладает одним минимальным элементом, который обозначим Nmin.

Из доказанной теоремы следует, что ЅNЅ= m + n = m + 2m = 3m , где m - число переходов, n - число позиций в примитивной системе; ЅNminЅ= 1 + 1 = 2 .

В дальнейшем элементы структур СП будем называть СП-структурами, а число элементарных сетей, которое включает максимальный элемент полной структуры - рангом структуры.

Теорема 3.2. Полная структура СП ранга  r включает все структуры СП с рангом

ri  <  r .

Доказательство. Для доказательства данной теоремы необходимо показать, что полная СП-структура ранга r  содержит примитивные СП-структуры, включающие по r-1, r-2,...,2 элементарных сетей, которые в свою очередь являются максимальными элементами структур СП ранга r-1,...,2.

Докажем включение в структуру СП ранга r примитивной СП с r-1 элементарными сетями. Очевидно, что , так как NPR ранга r содержит на одну элементарную сеть больше NPR ранга r-1. Следовательно, для перехода от к  необходимо выполнить три операции объединения между двумя элементарными сетями, например, ti и tj :

1) pre(ti)  И pre(tj) = pre(tij) ,

2) post(ti)  И  post(tj) = post(tij) ,                                                                  (3.1)

3) ti  И  tj  =  ti j .

В результате данных преобразований мы получили элемент полной структуры ранга r , но содержащей только  r-1 элементарных сетей.

Аналогично можно построить ,  и т.д.

Следовательно, теорема доказана.

Операцию понижения ранга структуры в соответствии с выражением (3.1) в дальнейшем будем называть сверткой.

            Рассмотрим пример. Пусть дана СП N, представленная на рис.3.1. Построим для данной СП все возможные нижние и верхние грани. Для этого при построении элементов, принадлежащих нижним граням, будем выполнять операцию принадлежащих верхним граням - операцию разделения. Движение от СП N вверх и вниз на рис.3.2 отображено пунктирными дугами. Очевидно, что элемент, имеющий значение k=2 (|N20|=2), является минимальным (N20 = Nmin ), а элемент, имеющий k=6 (ЅN1Ѕ= 6 ) - максимальным (N1 = Nmax ). Следовательно, структура СП, изображенная на рис.3.2, является полной. Наименьшей нижней гранью для N1 является грань 5-го уровня, которая включает СП-структуры с N2  по

Обратите внимание на лекцию "2.10 Антициклон".

N6 . Все данные структуры могут быть получены из СП-структуры Nmax путем выполнения одной операции объединения. Наибольшей нижней гранью для элемента Nmin является грань 3-го уровня, которая включает СП-структуры с N15 по N19 . Все данные структуры могут быть получены из Nmin  путем выполнения одной операции разделения. Из рис.3.2 видно, что ранг построенной структуры равен 2. Как подмножество в данную структуру входит структура с рангом 1 (элементы N19 и N20). Элементы данной структуры характеризуются тем, что они имеют либо наим.верхн. грань, либо наиб.нижн. грань. Такую структуру будем называть вырожденной.

На рис.3.2 приняты следующие обозначения: Spi - число головных позиций; Spj - число хвостовых позиций; s1=1 и s2=2 - веса головных и хвостовых  позиций, соответственно.

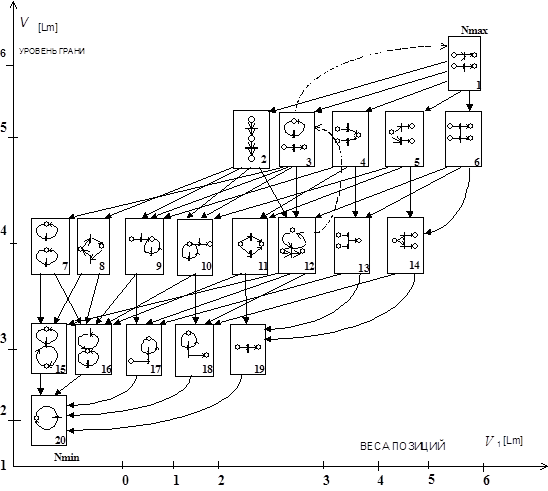
 Рис.3.2. Диаграмма множества СП-структур ранга 2:

                                 n[ Lm ] = | N | ; n₁ [ Lm ] = s₁ Sp_i + s₂ S p_j .