Теорема - Задача достижимости сводится к задаче активности

Теорема  Задача достижимости сводится к задаче активности.

Для доказательства основного утверждения раздела покажем следующее.

Теорема 5.6. Задача активности одного перехода сводится к задаче достижимости.

Доказательство того, что задача активности одного перехода сводима к задаче достижимости, опирается на проверку достижи­мости любой из конечного множества максимальных пассивных для t_j подмаркировок. Сеть Петри не активна для перехода t_j тогда и только тогда, когда достижима некоторая маркировка, в которой переход t_j не запускаем и не может стать запускаемым. Марки­ровка такого вида называется пассивной для t_j. Для любой марки­ровки μ можно проверить, является ли она пассивной для t_j, по­строением дерева достижимости с корнем μ и проверкой, можно ли

где-либо в дереве запустить переход t_j. Если нельзя, то μ массивна для t_j. Проверка активности t_j в таком случае требует проверки достижимости какой-либо пассивной для t_j маркировки.

В общем случае, однако, может существовать бесконечное число пассивных для t_j маркировок и бесконечное множество маркиро­вок, в котором находятся пассивные для t_j маркировки. Заметив два свойства, сведем множество маркировок, которые необходимо проверить для достижимости, к конечному числу. Во-первых, если маркировка μ пассивна для t_j, то и любая маркировка μ' μ пас­сивна для t_j. (Любая последовательность запусков, возможная из μ', возможна также из μ, поэтому если μ' может привести к запуску t_j , то это может и μ.) Во-вторых, маркировки некоторых позиций не будут влиять на пассивность для t_j данной маркировки, поэтому маркировки этих позиций являются «несущественными», они могут быть произвольными. Заимствуя прием из построения дерева дости­жимости, заменим «несущественные» компоненты на ω, показывая, что в этих позициях может быть произвольно большое число фишек, не влияющих на пассивность маркировки для t_j. Теперь, поскольку любая μ'  μ пассивна для t_j, если μ пассивна для t_j, нам не нужно рассматривать позиции p_i с μ(p_i)=. Это означает, что мы приме­няем задачу достижимости подмаркировки с P^’ = P_i |μ(P_i) ω}

Рассмотрим в качестве примера сеть Петри на рис. 5.7. Марки­ровки (2, 0), (1, 0), (0, 0), (0, 1), (0, 2), (0, 3),... являются пассивными для t₂ , но их можно представить конечным образом множеством {(2, 0), (1, 0), (0, ω)}.

Рекомендуемые материалы

Хэк  показал, что для сети Петри С существует такое конечное множество D_t маркировок (расширенных, т. е. включающих ω), что С активна тогда и только тогда, когда никакая марки­ровка из D_t недостижима. Если маркировка из D_t содержит ω, тогда подразумевается достижимость подмаркировки.

Более того, D_t можно эффективно вычислять. Поскольку D_t конечно, не- ω -компоненты имеют верхнюю границу b. Граница b определяется как такое наименьшее число, что если пассивна для t_j любая маркировка μ, такая, что μ(p_i)  b + 1 для всех p_i то является пассивной для t_j и подмаркировка μ', такая, что μ'(p_i) = μ(p_i), если μ(р_i) < b, и μ'(p_i) = ω, если μ(р_i) = b + 1. При таком определении b можно построить D_t следующим образом.

Вычислить b. Начать с b = 0, увеличивать b до тех пор, пока не окажется, что b удовлетворяет описанному определению границы. Проверка каждого b требует проверки всех (b + 2)n маркировок с компонентами, меньшими или равными b+1.

Вычислить D_t проверкой всех маркировок и подмаркировок с компонентами, не превышающими b или равными ω. D_t — это множество пассивных для t_j маркировок из множества (b + 2)n маркировок.

Построив D_t, можно рассматривать задачу достижимости под­маркировки для каждого элемента D_t. Если какой-либо элемент D_t достижим из начальной маркировки, сеть Петри неактивна, если же никакой элемент D_t недостижим - сеть Петри активна.

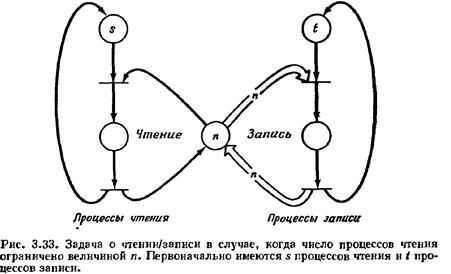
Существует несколько вариантов задачи о чтении/записи , однако основная структура их остается неизменной. Имеются про­цессы двух типов: процессы чтения и процессы записи. Все процес­сы совместно используют общий файл или переменную или элемент данных. Процессы чтения не изменяют объект в отличие от процес­сов записи. Таким образом, процессы записи должны взаимно ис­ключать все другие процессы чтения и записи, в то время как не­сколько процессов чтения могут иметь доступ к разделяемым дан­ным одновременно. Задача состоит в определении структуры управ­ления, которая не приведет к тупику и не допустит нарушения критерия взаимного исключения.

Лекция "Насосная эксплуатация скважин" также может быть Вам полезна.

На рис. 3.33 иллюстрируется решение задачи в том случае, когда количество процессов чтения ограничено величиной n. Если в системе количество процессов чтения не ограничено, то только n процессов могут выполняться в одно и то же время.

Проблема возникает в том случае, если количество процессов чтения не ограничено и мы хотим предоставить возможность не­

ограниченному количеству процессов читать одновременно.

В этом случае можно утверждать, что возникает необходимость хранения количества читающих процессов. При инициализации каждого процесса чтения в счетчик добавляется единица, а по окончании про­цесса единица

вычитается. Это легко моделируется позицией, в которой количество фишек равно количеству процессов чтения. Однако, для того, чтобы предоставить процессу записи возможность приступить к записи, необходимо, чтобы счетчик был нулевым, т. е. соответствующая позиция была бы пустой. В сетях Петри нет механизма, который бы осуществлял проверку на нуль неограни­ченной позиции [1]К Таким образом, оказывается, что задача о чтении/записи с неограниченным числом процессов чтения не может быть решена с помощью сетей Петри. Это первый случай, когда мы столк­нулись с тем, что сети Петри не способны моделировать все системы.