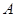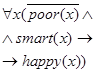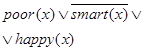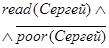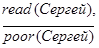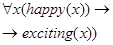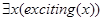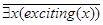Методы поиска решений
6.1. Методы поиска решений на основе
исчисления предикатов
Традиционной логикой называют формальную систему, предложенную Аристотелем более 2500 лет назад. Аристотель стремился установить и формально записать способы, с помощью которых можно было бы установить правильность рассуждений в разумной полемике. Множества правил, определяющих, какие умозаключения могут быть получены из множества суждений, он назвал силлогизмом. В данном случае под суждением понимается законченная мысль, которую можно выразить на естественном языке в одной из следующих четырех форм:
• все X являются Р — ("Х)Р(Х);
• никакой X не является Р — ("Х)ØР(Х);
• некоторые из X являются Р — ($Х)Р(Х);
• некоторые из Х не являются Р — ($Х)ØР(Х).
Каждое правило силлогизма определяет переход от предпосылок к заключению, являющемуся интуитивно очевидным. Силлогизм изначально предназначен для управления разумной дискуссией на естественном языке. Как формальная теория, он чрезмерно сложен и неполон. Силлогизм можно назвать логикой классов, которая не содержит понятия дополнения класса. Например, определив класс А (допустим, субъекты, являющиеся водителями автомобилей), мы не можем построить его дополнение (т.е. установить всех лиц, которые не являются водителями).
Будучи тесно связанным с естественным языком, силлогизм иногда приводит к абсурдным результатам, в частности, не допуская логическую эквивалентность двух способов выражения одной и той же мысли. Силлогизм неполон в том смысле, что он не позволяет осуществлять логические выводы, в которых затрагиваются вопросы существования элемента некоторого класса.
Рекомендуемые материалы
Последователи Аристотеля, основываясь на силлогизме, сформулировали принципы дедуктивного вывода для высказываний, которые находятся на более высоком уровне абстракции по сравнению с суждениями. Наиболее известными из этих правил являются следующие:
1. Modus Ponendo Ponens: «Если истинна импликация  и А истинно, то В истинно».
и А истинно, то В истинно».
2. Modus Tollendo Tollens: «Если истинна импликация  и В ложно, то А ложно».
и В ложно, то А ложно».
3. Modus Ponendo Tollens: «Если А истинно и конъюнкция  имеет результатом ложь, то В ложно».
имеет результатом ложь, то В ложно».
4. Modus Tollendo Ponens: «Если А ложно и дизъюнкция  истинна, то В является истиной».
истинна, то В является истиной».
На основе этих правил сформулировано правило «цепного заключения», весьма удобное для вывода в системе исчисления высказываний.
5. Цепное заключение: «Если истинна импликация  и истинна импликация
и истинна импликация  , то импликация
, то импликация  является истинной».
является истинной».
Рассмотрим пример вывода с применением этих правил. Пусть заданы следующие посылки:
1.  «Если растут мировые цены на топливно-энергетические ресурсы, то увеличиваются поступления в бюджет».
«Если растут мировые цены на топливно-энергетические ресурсы, то увеличиваются поступления в бюджет».
2.  «Если наблюдается рост производства или увеличиваются поступления в бюджет, то следует увеличение производства или укрепление рубля».
«Если наблюдается рост производства или увеличиваются поступления в бюджет, то следует увеличение производства или укрепление рубля».
3.  «Если растут мировые цены на топливно-энергетические ресурсы, то увеличиваются поступления в бюджет, из чего следует, что при росте цен на сырье или при увеличении поступлений в бюджет происходит рост производства или увеличение бюджета».
«Если растут мировые цены на топливно-энергетические ресурсы, то увеличиваются поступления в бюджет, из чего следует, что при росте цен на сырье или при увеличении поступлений в бюджет происходит рост производства или увеличение бюджета».
Используя Modus Ponendo Ponens, из посылок 1 и 3 можно вывести следующее заключение.
4.  «Если растут мировые цены на топливно-энергетические ресурсы или увеличиваются поступления в бюджет, то происходит рост производства или увеличение бюджета».
«Если растут мировые цены на топливно-энергетические ресурсы или увеличиваются поступления в бюджет, то происходит рост производства или увеличение бюджета».
Из посылок 4 и 2 с помощью цепного заключения можно получить посылку 5.
5.  «Если растут мировые цены на топливно-энергетические ресурсы или увеличиваются поступления в бюджет, то происходит рост производства или укрепление рубля».
«Если растут мировые цены на топливно-энергетические ресурсы или увеличиваются поступления в бюджет, то происходит рост производства или укрепление рубля».
Таким образом, применяя правила логического вывода, получаем новые логические формулы на основании исходных. При значительном количестве исходных данных возможно получение большого количества цепочек вывода, результаты которых могут противоречить друг другу. Подобные проблемы должны быть корректно решены в конкретных интеллектуальных системах при организации управления стратегией логического вывода.
Проблема доказательства в логике состоит в нахождении истинностного значения заключения В, если предполагается истинность исходных посылок  , что записывается в виде:
, что записывается в виде:  |–В. Знак |– в доказательствах и выводах следует читать «верно, что» или «можно вывести».
|–В. Знак |– в доказательствах и выводах следует читать «верно, что» или «можно вывести».
Существуют два основных метода решения проблемы доказательства в логике: семантический и синтаксический.
Семантический метод состоит в следующем. Можно перечислить все атомы, входящие в формулы  , В, и составить таблицу истинности для всевозможных комбинаций значений этих атомов. Затем следует осуществить просмотр полученной таблицы, чтобы проверить, во всех ли ее строках, где формулы
, В, и составить таблицу истинности для всевозможных комбинаций значений этих атомов. Затем следует осуществить просмотр полученной таблицы, чтобы проверить, во всех ли ее строках, где формулы  имеют значения «истина», формула В также имеет значение «истина». Этот метод применим всегда, но может оказаться слишком трудоемким.
имеют значения «истина», формула В также имеет значение «истина». Этот метод применим всегда, но может оказаться слишком трудоемким.
При синтаксическом методе доказательства сначала записывают посылки и, применяя к ним правила вывода, стараются получить из них другие истинные формулы. Из этих формул и исходных посылок выводят последующие формулы, и этот процесс продолжают до тех пор, пока не будет получено требуемое заключение (заметим, что это не всегда возможно). Этот процесс, по сути дела, и является логическим выводом.
Исчисление предикатов (ИП) обеспечивает основу для формализации теории логического вывода. Возможность логически выводить новые правильные выражения из набора истинных утверждений – это важное свойство ИП.
Говорят, что интерпретация, которая делает предложение истинным, удовлетворяет этому предложению. Если интерпретация удовлетворяет каждому элементу набора выражений, то говорят, что она удовлетворяет набору. Выражение Х логически следует из набора выражений S ИП, если каждая интерпретация, удовлетворяющая S, удовлетворяет и Х. Это утверждение делает основание для проверки правильности правил вывода: функция логического вывода должна производить новые предложения, которые логически следуют из данного набора предложений ИП.
Важно верно понимать значения слов «логически следует»: логическое следование выражения Х из S означает, что оно должно быть истинным для каждой интерпретации, которая удовлетворяет первоначальному набору выражений S. Это означает, например, что любое новое выражение ИП, добавленное к «миру блоков» должно быть истинным в этом мире. Оно должно быть истинным и при любой другой интерпретации, которую мог бы иметь этот набор выражений.
Термин «логически следует» вовсе не означает, что Х выведено из S, или что его можно вывести из S. Это просто означает, что Х истинно для каждой интерпретации, которая удовлетворяет S. Однако системы предикатов могут иметь бесконечное число возможных интерпретаций, поэтому практическая необходимость проверять все интерпретации возникает очень редко. В вычислительном отношении правила вывода позволяют определить, когда выражение как компонент интерпретации логически следует из этой интерпретации.
Понятие «логически следует» обеспечивает формальное основание для доказательства разумности и правильности правил вывода.
Иногда значение конкретной логической формулы не зависит от значений входящих в них атомов. Правильно построенные логические формулы, значением которых будет «истина» при любых значениях входящих в них атомов, называются тавтологиями. Тавтологии, или теоремы логики, обладают следующим свойством: если вместо всех вхождений некоторого атома в тавтологию подставить произвольную логическую формулу, то снова будет получена истинная формула. Эта новая формула называется частным случаем исходной формулы, или результатом подстановки.
Правило подстановки. Если  — тавтология и вместо всех вхождений формулы А в С подставить формулу В, то
— тавтология и вместо всех вхождений формулы А в С подставить формулу В, то  — тавтология. Для обозначения тавтологий используется символ
— тавтология. Для обозначения тавтологий используется символ  |=, который читается «общезначимо» или «всегда истинно».
|=, который читается «общезначимо» или «всегда истинно».
Примеры тавтологий:
|=  ;
;
|= ;
;
|= .
.
Докажем то, что первая приведенная тавтология (Modus Ponendo Ponens) всегда будет иметь значение «истина», для чего построим сокращенную таблицу истинности (табл. 6.1).
Таблица 6.1
Таблица истинности для доказательства тавтологии
|
|
|
|
|
| F F T T | B B T T | B B F F | T T T T |
В приведенной таблице Т — истина, F — ложь. Значение импликации совпадает со значением второго аргумента в том случае, если первый аргумент имеет значение Т, поэтому в первых двух строках второго столбца присутствует второй аргумент — В, значение которого может быть произвольным. Конъюнкция  при истинном А также будет иметь результат, совпадающий со значением В. Последний столбец таблицы комментариев не требует, так как приведенные в нем результаты очевидны.
при истинном А также будет иметь результат, совпадающий со значением В. Последний столбец таблицы комментариев не требует, так как приведенные в нем результаты очевидны.
Попробуем установить является ли эта же формула тавтологией синтаксическим методом. Для этого раскроем все скобки и убедимся, что результат упрощается до формул с очевидными значениями истинности:
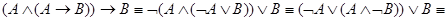
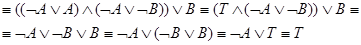
Помимо использования тавтологий и подстановок полезным средством для вывода является эквивалентность. Необходимо уметь правильно осуществлять замену взаимно эквивалентных формул. Например, можно подставить  вместо
вместо  , так как
, так как  .
.
Эквивалентность  можно заменить двусторонней импликацией
можно заменить двусторонней импликацией  , так как эти выражения имеют одну и ту же таблицу истинности. Отсюда можно сделать вывод, что логическая эквивалентность — это импликация в обоих направлениях. Эквивалентность можно привести в конъюнктивную нормальную форму (КНФ), которая имеет вид:
, так как эти выражения имеют одну и ту же таблицу истинности. Отсюда можно сделать вывод, что логическая эквивалентность — это импликация в обоих направлениях. Эквивалентность можно привести в конъюнктивную нормальную форму (КНФ), которая имеет вид:  . Если в этом выражении раскрыть скобки, получим дизъюнктивную нормальную форму (ДНФ):
. Если в этом выражении раскрыть скобки, получим дизъюнктивную нормальную форму (ДНФ):  . Другими словами, если А и В эквивалентны, то они либо оба истинны, либо оба ложны.
. Другими словами, если А и В эквивалентны, то они либо оба истинны, либо оба ложны.
Примеры тавтологий с эквивалентностями:
|=  ;
;
|= ;
;
|= ;
;
|= .
.
В процедурах логического вывода эквивалентности можно использовать двумя способами:
1) расписывать в виде двух отдельных импликаций;
2) использовать при заменах.
При этом важно понимать отличие замены от подстановки, которое состоит в следующем: если  , то А можно заменить на В в любом вхождении в формулу С, не меняя ее значения, причем замену не обязательно осуществлять во всех вхождениях.
, то А можно заменить на В в любом вхождении в формулу С, не меняя ее значения, причем замену не обязательно осуществлять во всех вхождениях.
В противовес тавтологиям в логике существуют противоречия — формулы, значением которых всегда будет «ложь» независимо от значений входящих в них атомов. Примером является выражение  при любом значении В.
при любом значении В.
Множество ППФ для некоторой предметной области называется теорией заданной области знаний, а каждая отдельная ППФ именуется аксиомой. Цель построения теории заключается в описании нужных знаний наиболее экономичным способом. Если удается построить теорию, которая адекватно описывает заданную область знаний, то все истинные факты из области интерпретации будут следствиями аксиом этой теории, другими словами, их можно будет вывести из множества ППФ. Соответственно ложные факты не будут следствиями теории, следовательно, их нельзя будет получить путем логического вывода на основании аксиом данной теории. Теорию называют полной, если все истинные факты являются следствиями этой теории. Это означает, что каждая истинная для данной теории ППФ может быть доказана на основании ее аксиом.
Про теорию говорят, что она является синтаксически последовательной (непротиворечивой), если из аксиом теории невозможно вывести противоречие. Теория, в которой можно доказать и Р, и  , непоследовательна.
, непоследовательна.
В качестве примера рассмотрим построение теории и ее проверку на полноту и непротиворечивость для следующего фрагмента знаний:
«Если у Вас нету дома,
Пожары ему не страшны,
И жена не уйдет к другому,
Если у Вас нет жены».
Постараемся обойтись средствами логики высказываний и начнем с формирования области интерпретации. Для этого введем обозначения:
А — «У Вас есть дом»
B — «Дом может сгореть»
С — «У Вас есть жена»
D — «Жена может уйти к другому»
На основе этих четырех высказываний построим логические формулы:
 ,
,
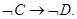
Кроме логических формул, выражающих связь фактов, любая теория содержит истинные факты, на основе которых становится возможным конкретная интерпретация ППФ. Допустим, что в нашей теории такими фактами являются А, В,  ,
,  .
.
Полученная теория является полной и последовательной, поскольку каждый факт этой теории выводится из остальных аксиом, при этом не возникнет противоречия. Доказать это несложно как семантическим, так и синтаксическим способом, однако для более сложных областей знаний необходимо использовать определенные стратегии доказательства, позволяющие преодолеть хаотичность процессов логического вывода.
Кратко рассмотрим три основные стратегии доказательства:
• доказательство с введением допущения;
• доказательство методом «от противного» (приведение к противоречию);
• доказательство методом резолюции.
Доказательство с введением допущения. Для доказательства импликации вида  допускается, что левая часть импликации истинна, т.е. А принимается в качестве дополнительной посылки, после чего делают попытки доказать правую часть В. Такая стратегия доказательства часто применяется в геометрии при доказательстве теорем.
допускается, что левая часть импликации истинна, т.е. А принимается в качестве дополнительной посылки, после чего делают попытки доказать правую часть В. Такая стратегия доказательства часто применяется в геометрии при доказательстве теорем.
Теорема 1. А ├ В тогда и только тогда, когда ├ .
.
Эта теорема утверждает, что доказуемость заключения В при допущении истинности А эквивалентна доказуемости импликации  без дополнительных допущений. Справедливость данной теоремы следует из приведенной ранее таблицы истинности (см. табл. 2.2).
без дополнительных допущений. Справедливость данной теоремы следует из приведенной ранее таблицы истинности (см. табл. 2.2).
Теорема 2.  ├ В тогда и только тогда, когда ├
├ В тогда и только тогда, когда ├ .
.
Эта теорема выводится из предыдущей и того факта, что посылки  истинны только тогда, когда истинна их конъюнкция.
истинны только тогда, когда истинна их конъюнкция.
Пример. Требуется доказать  ,Р├Q. В соответствии с теоремой 2 получим ├
,Р├Q. В соответствии с теоремой 2 получим ├ . Применив эквивалентность вида
. Применив эквивалентность вида  , откуда имеем в силу теоремы 2 ├
, откуда имеем в силу теоремы 2 ├ ├
├ .
.
Приведение к противоречию. Этот метод доказательства, предложенный К. Робинсоном в 1960-х гг., вывел исследования в области искусственного интеллекта на новый уровень. Метод обусловил появление обратных выводов и эффективных способов выявления противоречий. Суть его состоит в следующем. Например, требуется доказать  . Вместо этого можно попытаться доказать
. Вместо этого можно попытаться доказать  , используя эквивалентность. Такое доказательство можно провести двояко, а именно: или допустить А и доказать затем В (это будет прямой вывод), или сделать допущение о том, что В — ложно, после чего сделать попытку опровергнуть посылку А (обратный вывод). Приведение к противоречию — комбинация прямого и обратного вывода, т. е. для доказательства
, используя эквивалентность. Такое доказательство можно провести двояко, а именно: или допустить А и доказать затем В (это будет прямой вывод), или сделать допущение о том, что В — ложно, после чего сделать попытку опровергнуть посылку А (обратный вывод). Приведение к противоречию — комбинация прямого и обратного вывода, т. е. для доказательства  можно одновременно допустить А и
можно одновременно допустить А и  (посылка истинна, а заключение — ложно):
(посылка истинна, а заключение — ложно):
 .
.
В процессе доказательства можно двигаться по пути, который начинается от А или от  . Если В выводимо из А, то, допустив истинность А, мы доказали бы В. Поэтому, сделав допущение
. Если В выводимо из А, то, допустив истинность А, мы доказали бы В. Поэтому, сделав допущение  , получим противоречие. Если вывод приведет к успеху (т.е. противоречие не будет получено), это будет свидетельствовать о несовместимости либо противоречивости исходных посылок. Мы также не получим противоречия, если доказываемое предложение
, получим противоречие. Если вывод приведет к успеху (т.е. противоречие не будет получено), это будет свидетельствовать о несовместимости либо противоречивости исходных посылок. Мы также не получим противоречия, если доказываемое предложение  является ложным.
является ложным.
Правила вывода обеспечивают создание новых предложений ИП на основе данных предложений. Следовательно, правила вывода производят новые предложения, основанные на новой синтаксической форме данных логических утверждений. Если каждое предложение Х, полученное с помощью некоторого правила вывода на множестве логических выражений S, также логически следует из S, то говорят, что правило вывода обосновано.
Доказательство методом резолюции. Этот метод считается более трудным для понимания, однако имеет важное преимущество перед другими: он легко формализуем. В основе метода лежит тавтология, получившая название «правило резолюции»:
|=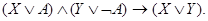
Теоремы 1 и 2 позволяют записать это правило в следующем виде:
 ,
,  |–
|– ,
,
что дает основания утверждать: из посылок  и
и  можно вывести
можно вывести  .
.
В процессе логического вывода с применением правила резолюции выполняются следующие шаги.
1. Устраняются операции эквивалентности и импликации.
2. Операция отрицания продвигается внутрь формул с помощью законов де Моргана
3. Логические формулы приводятся к дизъюнктивной форме.
Правило резолюции содержит в левой части конъюнкцию дизъюнктов, поэтому приведение посылок, используемых для доказательства, к виду, представляющему собой конъюнкции дизъюнктов, является необходимым этапом практически любого алгоритма, реализующего логический вывод на базе метода резолюции. Метод резолюции легко программируется, это одно из важнейших его достоинств.
Предположим, нужно доказать, что если истинны соотношения  ,
,  и
и  , то можно вывести формулу
, то можно вывести формулу  . Для этого нужно выполнить следующие шаги.
. Для этого нужно выполнить следующие шаги.
1. Приведение посылок к дизъюнктивной форме:
 ,
,  ,
,  .
.
 .
.
Полученная конъюнкция справедлива, когда  и
и  одновременно истинны.
одновременно истинны.
3. Применение правила резолюции:
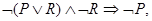
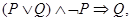
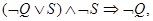
 (противоречие или «пустой дизъюнкт»).
(противоречие или «пустой дизъюнкт»).
Итак, предположив ложность выводимого заключения, получаем противоречие, следовательно, выводимое заключение является истинным, т.е.  выводимо из исходных посылок.
выводимо из исходных посылок.
Именно правило резолюции послужило базой для создания языка логического программирования PROLOG. По сути дела, интерпретатор языка PROLOG самостоятельно реализует вывод, формируя ответ на вопрос пользователя, обращенный к базе знаний.
В логике предикатов для применения правила резолюции предстоит осуществить более сложную унификацию логических формул в целях их приведения к системе дизъюнктов. Это связано с наличием дополнительных элементов синтаксиса, в основном кванторов, переменных, предикатов и функций.
Унификация. Чтобы применять правила вывода, система вывода должна уметь определять, когда два выражения являются эквивалентными (равносильными). В исчислении высказываний это тривиально: два выражения равносильны тогда и только тогда, когда они синтаксически идентичны. В ИП определение равносильности двух предложений усложняется наличием переменных. Существуют правила, позволяющие заменять переменные под знаком квантора всеобщности (") термами из области определения. Необходимо определить процесс замены переменных, при которых несколько выражений могут стать идентичными. Унификация определяет условия, при которых два (или больше) выражения ИП могут быть эквивалентными (равносильными).
Унификация – это алгоритм определения необходимых подстановок с целью приведения в соответствие двух выражений ИП. Унификация и такие правила вывода как modus ponens, позволяют делать выводы на множестве логических утверждений. Для этого база данных должна быть выражена в соответствующей форме. Важный аспект этой формы заключается в требовании, чтобы все переменные стояли под знаком квантора всеобщности. Это обеспечивает в выполнении подстановок. Переменные, стоящие под квантором существования ($) можно устранить из предложений, заменив их константами, обеспечивающими истинность предложения. Например, $х родитель (х, Олег) может быть заменено выражением родитель (Роман, Олег) или (Надежда, Олег), принимая во внимание, что Роман и Надежда являются родителями Олега в этой интерпретации.
Процесс удаления переменных, связанных квантором существования, усложняется тем, что значение этих подстановок может зависеть от значения других переменных. Например, в высказывании  мать (х,у) значение переменной у под квантором $ зависит от значения х. Сколемизация – это замена каждой переменной, связанной квантором существования, функцией нескольких переменных, которая возвращает соответствующую константу. В примере у можно заменить сколемовской функцией f от х, получаем предикат "х мать (х, f(x)). Сколемизация также позволяет связывать переменные, стоящие под квантором всеобщности, с константами.
мать (х,у) значение переменной у под квантором $ зависит от значения х. Сколемизация – это замена каждой переменной, связанной квантором существования, функцией нескольких переменных, которая возвращает соответствующую константу. В примере у можно заменить сколемовской функцией f от х, получаем предикат "х мать (х, f(x)). Сколемизация также позволяет связывать переменные, стоящие под квантором всеобщности, с константами.
При создании алгоритма унификации, который вычисляет подстановки, возникают следующие проблемы.
1. Так как константу можно использовать в качестве подстановки для переменной, любая константа рассматривается как «базовый экземпляр» и не может быть заменена. Нельзя также два различных «базовых экземпляра» использовать в качестве подстановки для одной и той же переменной.
2. Переменная не может быть унифицирована с термом, содержащим ее. Поэтому переменная х не может быть заменена на f(x).
Процесс решения задачи требует ряда выводов и, следовательно, ряда последовательных унификаций. Логические решающие устройства задач должны поддерживать согласованность установок для переменных. Важно, чтобы любая унифицирующая подстановка была сделана, согласовано по всем вхождениям этой переменной во все выражения. А выражения должны быть приведены в соответствие друг другу.
3. Если переменная связана, все последующие унификации и процедуры вывода должны учитывать это. Если переменная связана с константой, ее уже нельзя связывать с другим термом при последующих унификациях. Если переменная х1 использовалась в качестве подстановки для х2, а затем была заменена константой, то в х2 тоже необходимо отразить это связывание.
4. Унификатор должен быть максимально общим, т.е. для любых двух выражений должен быть найден наиболее общий унификатор. Это очень важно, так как при потере общности в процессе решения уменьшается вероятность достижения окончательного решения или такая возможность исчезает.
Алгоритм унификации предикатных логических формул включает следующие шаги.
1. Исключение операций эквивалентности.
2. Исключение операций импликации.
3. Внесение операций отрицания внутрь формул.
4. Исключение кванторов существования. Это может произойти на шаге 3 вследствие применения законов де Моргана, а именно: в результате отрицания $ меняется на ", но при этом может произойти и обратная замена. Тогда для исключения $ поступают следующим образом: все вхождения некоторой переменной, связанной квантором существования, например ($X), заменяются в формуле на новую константу, например а. Эта константа представляет собой некоторое (неизвестное) значение переменной X, для которого утверждение, записанное данной формулой, истинно. При этом важно то, что на все места, где присутствует X, будет подставлено одно и то же значение а, пусть оно и является неизвестным в данный момент. Такие константы называются сколемовскими, а операция — сколемизацией (по имени известного математика Сколема).
5. Кванторы общности выносятся на первые места в формулах. Это также не всегда является простой операцией, иногда при этом приходится делать переименование переменных.
6. Раскрытие конъюнкций, попавших внутрь дизъюнкций, т.е. бескванторную часть формулы привести к конъюнктивной нормальной форме (КНФ).
После выполнения всех шагов описанного алгоритма унификации можно применять правило резолюции. Обычно при этом осуществляется отрицание выводимого заключения, и алгоритм вывода можно кратко описать следующим образом: Если задано несколько аксиом (теория Тh) и предстоит сделать заключение о том, выводима ли некоторая формула Р из аксиом теории Тh, строится отрицание Р и добавляется к Тh, при этом получают новую теорию Тh1. После приведения  и аксиом теории к системе дизъюнктов можно построить конъюнкцию
и аксиом теории к системе дизъюнктов можно построить конъюнкцию  и аксиом теории Тh. При этом существует возможность выводить из исходных дизъюнктов дизъюнкты-следствия. Если Р выводимо из аксиом теории Тh, то в процессе вывода можно получить некоторый дизъюнкт Q, состоящий из одной литеры, и противоположный ему дизъюнкт
и аксиом теории Тh. При этом существует возможность выводить из исходных дизъюнктов дизъюнкты-следствия. Если Р выводимо из аксиом теории Тh, то в процессе вывода можно получить некоторый дизъюнкт Q, состоящий из одной литеры, и противоположный ему дизъюнкт  . Это противоречие свидетельствует о том, что Р выводимо из аксиом Тh. Вообще говоря, существует множество стратегий доказательства, нами рассмотрена лишь одна из возможных — нисходящая.
. Это противоречие свидетельствует о том, что Р выводимо из аксиом Тh. Вообще говоря, существует множество стратегий доказательства, нами рассмотрена лишь одна из возможных — нисходящая.
Пример. Представим средствами логики предикатов следующий текст:
«Если студент умеет хорошо программировать, то он может стать специалистом в области информационных технологий».
«Если студент хорошо сдал экзамен по технологии программирования, значит, он умеет хорошо программировать».
Представим этот текст средствами логики предикатов первого порядка. Введем обозначения: X — переменная для обозначения студента; хорошо — константа, соответствующая уровню квалификации; Р(Х) — предикат, выражающий возможность субъекта X стать специалистом в области информационных технологий; Q(X, хорошо) — предикат, обозначающий умение субъекта X программировать с оценкой хорошо; R(Х, хорошо) — предикат, задающий связь студента X с экзаменационной оценкой по технологии программирования.
Теперь построим множество ППФ:
("Х)Q(Х, хорошо)®Р(Х).
("Х)R(Х, хорошо) ®Q(Х, хорошо).
Дополним полученную теорию конкретным фактом R(ива-нов, хорошо).
Выполним логический вывод с применением правила резолюции, чтобы установить, является ли формула Р(иванов) следствием вышеприведенной теории. Другими словами, можно ли вывести из этой теории факт, что студент Иванов станет специалистом в области информационных технологий, если он хорошо сдал экзамен по технологии программирования.
Доказательство.
1. Выполним преобразование исходных формул теории в целях приведения к дизъюнктивной форме:
($Х)  Q(Х,хорошо)ÙР(Х);
Q(Х,хорошо)ÙР(Х);
($Х)  R(Х,хорошо)ÚQ(Х,хорошо);
R(Х,хорошо)ÚQ(Х,хорошо);
R(иванов, хорошо).
2. Добавим к имеющимся аксиомам отрицание выводимого заключения
 Р(иванов).
Р(иванов).
3. Построим конъюнкцию дизъюнктов
($Х)  Q(Х, хорошо) Ú Р(Х) Ù
Q(Х, хорошо) Ú Р(Х) Ù Р(иванов) Þ
Р(иванов) Þ Q(иванов, хорошо),
Q(иванов, хорошо),
заменяя переменную X на константу иванов.
Результат применения правила резолюции называют резольвентой. В данном случае резольвентой является  Q(иванов).
Q(иванов).
4. Построим конъюнкцию дизъюнктов с использованием резольвенты, полученной на шаге 3:
($Х)  R(Х, хорошо)Ú(Х, хорошо) /
R(Х, хорошо)Ú(Х, хорошо) /  Q(иванов, хорошо) Þ
Q(иванов, хорошо) Þ  R(иванов, хорошо).
R(иванов, хорошо).
5. Запишем конъюнкцию полученной резольвенты с последним дизъюнктом теории:
 R(иванов, хорошо) / R(иванов, хорошо) ® F (противоречие). Следовательно, факт Р(иванов) выводим из аксиом данной теории.
R(иванов, хорошо) / R(иванов, хорошо) ® F (противоречие). Следовательно, факт Р(иванов) выводим из аксиом данной теории.
Для определения порядка применения аксиом в процессе вывода существуют следующие эвристические правила:
1. На первом шаге вывода используется отрицание выводимого заключения.
2. В каждом последующем шаге вывода участвует резольвента, полученная на предыдущем шаге.
Рассмотрим пример применения методов поиска решений на основе исчисления предикатов. Пример «интересная жизнь» взят из [6]. Заданы утверждения 1-4 в 1-м столбце таблицы 6.2. Требуется ответить на вопрос: «Существует ли человек, живущий интересной жизнью?» В виде предикатов эти утверждения записаны во 2-ом столбце таблицы. В третьем столбце таблицы записаны дизъюнкты.
Таблица 6.2
| Утверждения и заключение | Предикаты | Дизъюнкты |
| 1 | 2 | 3 |
| 1. Все небедные и умные люди счастливы |
|
|
| 2. Человек, читающий книги, - неглуп |
|
|
| 3. Сергей умеет читать и является состоятельным человеком |
|
|
| 4. Счастливые люди живут интересной жизнью |
|
|
Продолжение табл. 6.2
| 1 | 2 | 3 |
| 5. Заключение: Существует ли человек, живущий интересной жизнью? |
|
|
| 6. Отрицание заключения |
|
|
Одно из возможных доказательств (их более одного) дает следующая последовательность резольвент:
1.  Резольвентой дизъюнктов
Резольвентой дизъюнктов  и
и  является
является  .
.
"Опухолевые заболевания органов мошонки" - тут тоже много полезного для Вас.
2.  и
и  дают резольвенту
дают резольвенту  .
.
3.  и
и  -
-  .
.
4. Унифицируем  .
.
Резольвентой дизъюнктов  и
и  является
является  .
.
5. Дизъюнкты  и
и  дают пустую резольвенту.
дают пустую резольвенту.
Получение пустой резольвенты означает, что база данных выражений содержит противоречие и поэтому предположение о том, что существует человек, живущий интересной жизнью, верно.