Функции порождения

Лекция 11

4.6 Функции порождения для недетерминированных систем

            Параметрически инвариантное ограничение на множество вы­борочных переменных может быть охарактеризовано разными способами. Простое описание, рассмотренное в разд. 3.3, может ограничиться заданием функции выбора, определенной на соот­ветствующем множестве состояний. Хотя функция выбора явля­ется, вероятно, наиболее подходящим формальным аппаратом для задания ограничений в детерминированных системах, в которых порождение данных удобно описывать с помощью функции (4.20), для работы с недетерминированными системами функции выбора не годятся.

Традиционно с недетерминированными системами работают методами теории вероятностей. При этом основным понятием при описании ограничений на переменные является понятие вероятностной меры.

Из теории вероятностей хорошо известно, что любая веро­ятностная мера, скажем мера р, однозначно определяется функ­цией распределения

, (4.21)

При этом порождающая функция поведения  имеет вид

Рекомендуемые материалы

,(4.22)

где — условная вероятность при условии .    Чтобы    подчеркнуть, что  задает условные    вероятности, для обозначения вероятности   при заданном  вместо   используется стандартное обозначение .

4.7 Направленные системы с поведением

До сих пор мы рассматривали только нейтральные системы с поведением (базовые и порождающие). Для описания их направленных аналогов необходимо разбить соответствующее мно­жество выборочных переменных на два подмножества:

1) выборочные переменные, определяемые средой, т. е. вход­ные переменные [переменные , для которых ];

2)   остальные выборочные переменные, связанные с рассмат­риваемой маской.

Эти два подмножества выборочных переменных можно опре­делить, разбив заданную маску М на две подмаски. Пусть подмаска   определяет выборочные переменные, задаваемые сре­дой, а подмаска   — остальные. Тогда тройка

, (4.23)

для которой справедливо, что

(4.24)

определяет маску направленной системы с поведением.

D Согласно разбиения на  и  множество  идентификаторов выборочных переменных, определяемых М, разобьется на подмноже­ства  и . Кодирующая функция (3.6) будет заменена соответ­ственно на две функции

 (4.25)

и будут определены следующие два множества состояний:

(4.26)

необходимые для направленных систем. Функция поведения на­правленных систем имеет вид

,(4.27)

где  — это условная вероятность и,   следовательно,    вместо    записи можно использовать стандартную форму . Теперь можно определить направленную систему    с    поведением    как тройку

.(4.28)

Порождающая функция поведения для направленных систем может быть введена с помощью   разбиения  на два подмножества и , соответствующих порождаемым и порождающим переменным. Делается это точно так же, как было описано для М. Таким образом, порождающая маска для направленных систем задается четверкой

,(4.29)

где  — это разбиение М.    Снова   определяются   кодирующие функции (4.15), но  рассматривается   теперь   как разбиение . Множества  и  определяются формулами (4.16).

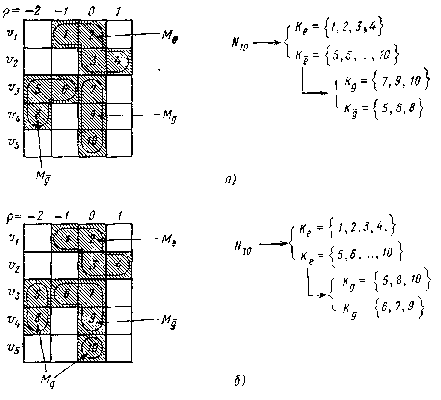
Рис. 4.4. Разбиения маски для направленной представляющей системы с полностью упорядоченным параметрическим множеством и  для обоих возможных порядков порождения данных

Теперь

,(4.30)

где  — это условная    вероятность, и, следовательно, в соответствии с традицией ее можно записать в виде . Для детерминированных систем  можно переписать в более удобном виде

,(4.31)

Люди также интересуются этой лекцией: 5. Автоматизация добычных процессов.

который представляет собой направленный аналог порождающей функции поведения, определенной (4.20). Если предположить, что смысл   определен, то направлен­ная порождающая система с поведением определяется тройкой

.(4.32) ▲

На рис. 4.4 показано разбиение маски    на    три подмаски  ,, (и соответствующее разбиение идентификаторов выборочных переменных) в предположении, что и — это входные переменные. На рис. 4.4,а и б показаны два варианта, соответст­вующие порождению данных в порядке возрастания и убывания значений параметра.

К.Р. № 11

            Опишите функции поведения для недетерминированных направленных систем.