Прямые методы решения СЛАУ, основанные на факторизации симметричной матрицы

ПРЕДОБУСЛАВЛИВАТЕЛИ.

1. Прямые методы решения СЛАУ, основанные на факторизации симметричной матрицы.

Как уже не раз отмечалось, лучшим предобуславливателем была бы матрица , однако для нахождения поправки  пришлось бы решать задачу , что так же трудно, как построить решение исходной задачи . Довольно просто решаются задачи с диагональными и треугольными матрицами. Например, задача  решается так: . А вот решение задачи с верхней треугольной матрицей , или

                                            .                                  (1)

Вначале из последнего уравнения находим , подставляем результат в ()-ое уравнение и выражаем . Из i-го уравнения найдем

                                                              (2)

Аналогично решается система  с нижней треугольной матрицей:

                                                                        (3)

Люди также интересуются этой лекцией: Лекция №5 Характеристика человека как элемента системы «Человек-среда» .

В формулах (2), (3) сумма полагается равной нулю, если нижний предел изменения индекса больше верхнего.

Другой, более сложный пример: задача  с матрицей, представленной в виде произведения нижней треугольной  и верхней треугольной . Эта задача решается в два этапа. Вначале по формуле (3) находим решение задачи , а затем по формуле (2) определяем  как решение задачи .

Заметим, что решение здесь строится за конечное число шагов, значит это прямые методы решения СЛАУ. Из-за легкости обращения диагональных и треугольных матриц возникает соблазн использовать их для конструкции предобуславливателя , и решать задачу для поправки прямым методом.

Отвлечемся на время от проблемы предобуславливания в итерационных схемах и рассмотрим прямые методы решения задачи , основанные на факторизации матрицы , т.е. на представлении ее в виде произведения легко обратимых матриц. Наиболее популярны два способа факторизации:

1) Разложение Холецкого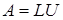

2) Тройная факторизация .