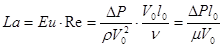Критериальные уравнения. Критерии и числа подобия

Критериальные уравнения. Критерии и числа подобия.

После приведения уравнения Навье-Стокса к следующему виду они стали содержать следующие типы переменных: 1) безразмерные независимые переменные ; 2) безразмерные зависимые переменные ; 3) безразмерные критерии – комплексы, состоящие из величин заданных по условиям однозначности  .

После приведения к безразмерному уравнению изменился характер уравнений. Уравнения приобрели обобщенный вид, т.к. одно и то же значение любого критерия может быть получено путем бесконечного варьирования входящих величин. Уравнения могут быть записаны в виде:

Критерии подобия могут быть двух видов: 1) состоящие из разноименных параметров;  2) имеющие периодический вид, т.к. представляют собой отношение одноименных параметров. Пример: для труб: .

Относительные переменные также могут быть двух видов:

1) отношение переменной к одноименной величине, заданной по условию однозначности: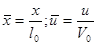

2) если по условию однозначности нельзя задать одноименную величину, то строится комплекс приводящий величину к безразмерному виду – число подобия: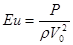

В  числа подобия входят определяемая величина. Критерий подобия состоит из заранее известных величин, заданных по условиям однозначности..

Рекомендуемые материалы

1) Критерий Рейнольдса  - определяет соотношение сил инерции и вязкости в однородном потоке. Это важнейший гидродинамический критерий для вынужденного движения. При движении потока в нем возникают возмущения, которые исходят от стенок канала или вносятся в поток извне. Влияние возмущений зависит от соотношения сил. Если преобладают силы вязкости возмущения гаснут и поток не меняет своей структуры. Если преобладают силы инерции возмущения развиваются дальше, поток меняет течение, изменяется его структура. Граница соотношения сил определяется по значению Re_кр. Если Re<Re_кр преобладают вязкие силы, Re>Re_кр – силы инерции. Re характеризует движение при соизмеримости инерции и вязкости. Если в потоке преобладает какой-то один вид сил характер перестает зависеть от величины Re. В этом случае говорят, что течение автомодельно относительно критерия Re.

2) Критерий гидродинамической гомохронности  - определяет соотношение между периодом темпа внешних воздействий на поток и периодом перестройки скоростного поля. Используют только для нестационарных задач. - время, за которое проходит частица, движущаяся со скоростью V₀, путь l₀. Если в задаче время подлежит определению, то рассматривается не критерий, а число Струхала: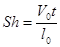

3) Критерий Фруда  - определяет соотношение между силами инерции и тяжести в потоке. Используется только в задачах, в которых гравитационные эффекты имеют важное значение. Однако в таких задачах часто сложно задать характерную скорость (при естественной конвекции), поэтому строится критерий, в котором исключается скорость:  - критерий Галилея.                                          При гравитационном движении важное значение имеет параметрический критерий: .

Причем ρ и ρ₀ – плотности не только в разных точках, но и в различных фазах.                                 - критерий Архимеда.

Люди также интересуются этой лекцией: 12 Процедуры.

При гравитационном течении однофазной жидкости движение возникает в результате расшире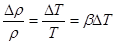ния:

 - коэффициент объемного расширения.

 - критерий Гросгофа.

4) Число Эйлера 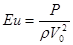 - определяет соотношение сил давления и сил инерции; определяемая величина; т.к. часто давление в потоке неизвестно, то больший интерес представляет определение перепада давления на рассматриваемом участке .

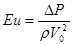
 - безразмерный коэффициент сопротивления при очень низких скоростях, когда течение ламинарное , , в этих случаях рассматривают число Лагранжа, которое принимает постоянное значение: