Линейный гармонический осциллятор

Линейный гармонический осциллятор

Линейным гармоническим осциллятором называется система, потенциальная энергия которой квадратично зависит от координаты:

.

Здесь m — масса частицы, а ω — собственная частота осциллятора. На рис. 11.1 зависимость (1)

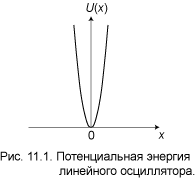
изображена графически. Кривая U(x) своей крутизной и бесконечно большой высотой напоминает потенциальную яму. Ниже мы увидим, что линейный осциллятор, действительно, проявляет некоторые свойства частицы в бесконечно высокой потенциальной яме. Например, он имеет бесконечное число дискретных уровней. Но в отличие от отвесных стенок ямы, потенциал осциллятора растёт плавно, и, как следствие, появляется некоторая вероятность обнаружить частицу достаточно далеко от начала координат. Плавная форма потенциала позволяет осциллятору при определённых условиях проявить свойства классической (не квантовой) частицы. Для этого достаточно, чтобы длина волны де Бройля была меньше характерных размеров области изменения потенциала. В случае потенциальной ямы, либо потенциального барьера, такая возможность полностью исключена, так как там потенциал меняется скачком в одной точке. Перейдём к количественному решению задачи.

Напишем одномерное уравнение Шредингера с потенциальной энергией (1):

.

У него нет естественных граничных условий. Дискретные уровни энергии получаются как следствие ограниченности волновой функции.

Рекомендуемые материалы

Преобразуем уравнение (2): вместо координаты x введём безразмерный аргумент

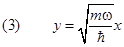
и вместо E — безразмерную энергию осциллятора

.

Легко убедиться, что обратная величина подкоренного выражения в (3) равна произведению комптоновской длины волны электрона  (1.3.1) и длины волны D = l/(2p) =c/w, соответствующей собственной частоте осциллятора. С принятыми обозначениями уравнение Шредингера принимает вид:

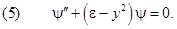
Здесь штрихами обозначено дифференцирование по координате y.

Квантовые свойства осциллятора имеют многочисленные приложения в атомной физике. Ниже мы рассмотрим два из них: влияние нулевых колебаний электромагнитного вакуума на функцию Планка и связанный с ними лэмбовский сдвиг метастабильного уровня атома водорода.

11.1 Решение волнового уравнения

Уравнение (5) решаем методом разложения в ряд с предварительным выделением множителя, быстро убывающего на больших расстояниях от начала координат. Обозначим посредством ψ_∞ волновую функцию при больших значениях аргумента: y ? ε. Ей соответствует асимптотическая форма уравнения Шредингера

.

Множитель  перед функцией появляется при двукратном дифференцировании экспоненты , а именно:

.

В области больших значений аргумента можно пренебречь единицей по сравнению с y² в множителе . Следовательно, рассматриваемая экспонента может служить асимптотическим приближением точного решения:

.

Решение уравнения (5) при произвольных значениях аргумента будем искать в виде

.

Согласно (5), функция f(y) удовлетворяет уравнению

.

Ищем решение в виде ряда:

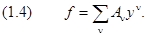
Дважды продифференцируем искомую функцию

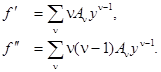
Подставив эти разложения в (1.3), получим бесконечную цепь линейных уравнений для коэффициентов разложения A_ν:

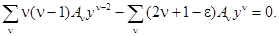
Соберем степени с одинаковыми показателями, для чего индекс первой суммы увеличиваем на два:

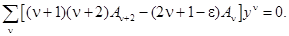
Сумма тождественно равна нулю, когда исчезает каждый коэффициент при y^ν. Отсюда вытекает рекуррентное соотношение для коэффициентов разложения (1.4):

.

Задав A₀ и A₁, мы получим все коэффициенты A_n, соответственно, с чётными и с нечётными номерами. Формальное решение задачи получено.

Теперь покажем, что условию ограниченности волновой функции удовлетворяет только конечная сумма, но не бесконечный ряд. Для этого покажем, что ряд, коэффициенты которого подчиняются условию (1.5), растёт быстрее, чем . Разложим экспоненту в ряд Тейлора:

.

Здесь ν принимает только чётные значения. Мы ввели обозначение

.

Отношение

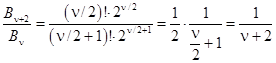
при больших значениях ν стремится к 1/ν. В то же время из (1.5) следует:

.

Теперь ясно, что функция, описываемая соотношением (1.5), растёт быстрее, чем экспонента (1.6). Следовательно, произведение (1.4) при больших значениях аргумента неограниченно возрастает. Поэтому физический смысл имеет только такое решение (1.3), в котором сумма (1.4) содержит лишь конечное число слагаемых.

Покажем, как требование конечности числа слагаемых приводит к дискретному спектру уровней осциллятора. Пусть n — номер последнего члена ряда (1.4), не равного нулю:

.

Из (1.5) вытекает связь между величиной энергетического уровня и его номером:

.

Итак, мы снова получили дискретные уровни энергии. Каждому уровню с номером n соответствует ровно одна волновая функция:

,

где

,

причём нижний предел равен нулю при чётном n и единице — при нечётном. Уровни энергии, согласно (4) и (1.7), принимают дискретный ряд значений:

.

Обратим внимание на то, что наименьшее из возможных значений энергии, равное

,

отлично от нуля. Это состояние соответствует так называемым нулевым колебаниям.

Рекуррентное соотношение (1.5) с учётом (1.7) принимает вид

.

Оно позволяет восстановить все коэффициенты суммы (1.8а) с точностью до общего множителя; последний может быть найден из условия нормировки волновой функции (1.8). Поскольку , то сумма (1.8а) — знакопеременная. Функция f_n является чётной при чётных значениях её номера n, и нечётной — при нечётных n. Она пропорциональна известным в математике полиномам Эрмита H_n(y). Выпишем для справки нормированную волновую функцию состояния осциллятора с номером n:

.

Приведём несколько первых полиномов Эрмита:

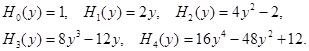
В общем случае

.

Исследуем полученное решение.

11.2 Свойства квантового осциллятора

Линейный осциллятор имеет эквидистантную систему уровней: разность энергий двух соседних уровней постоянна и равна . Именно такой квант энергии излучается или поглощается при переходе между соседними уровнями. На рис.11.2.1 слева приведены графики волновой функции для трёх первых значений n. По горизонтальной оси отложены значения безразмерного аргумента y.

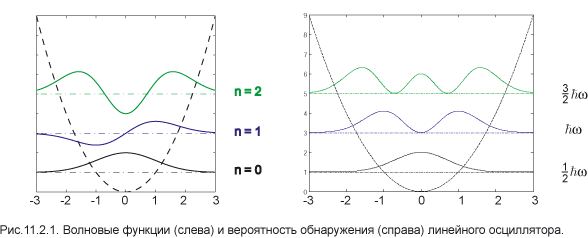
Парабола изображает потенциальную функцию, а горизонтальные прямые — значения энергетических уровней. Для удобства восприятия волновые функции сдвинуты по вертикальной оси.

Волновые функции линейного осциллятора и рассмотренной выше задачи о прямоугольной потенциальной яме имеют некоторые сходные черты. Во–первых, у них одинаково количество узлов. Здесь мы ещё раз встречаемся с проявлением осцилляционной теоремы, упомянутой в девятой главе. Так, волновая функция основного состояния ψ₀ не обращается в нуль ни в одной точке на прямой, а графики функций ψ₁ и ψ₂ пересекают горизонтальную ость, соответственно, один и два раза. Для остальных состояний имеет место тот же самый результат. Действительно, из теории специальных функций известно, что полином Эрмита n–го порядка H_n имеет ровно n корней. Во–вторых, квантовую частицу можно обнаружить и в области, запрещённой для движения в классической механике, что иллюстрирует график на рис.11.2.1 справа.

В состояниях с сильным возбуждением квантовый осциллятор приобретает свойства классической частицы. На рис. 11.2.2 схематически изображён график вероятности в

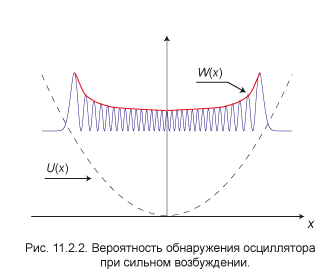
пределе . Пунктиром, как и выше, отмечена потенциальная кривая, а синим цветом — вероятность обнаружения. Функция W(x) быстро осциллирует, причём её огибающая (она обозначена на рисунке красным цветом) монотонно растёт от центра к периферии. Такой рост имеет аналогию в классической механике, когда вероятность обнаружения частицы на отрезке длиной Δx обратно пропорциональна её скорости V:

.

В точках поворота скорость обращается в нуль, поэтому там легче всего найти частицу. В самом деле, рассмотрим движение частицы по закону

.

Классическую вероятность обнаружения частицы на отрезке от x до x + dx определим как отношение времени прохождения отрезка

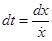
к половине периода колебаний:

.

Вероятность значительно увеличивается вблизи точек поворота . Для достаточно больших значений n в апертуру прибора с конечной разрешающей способностью попадает много горбов, поэтому осцилляции волновой функции в классическом пределе незаметны. Но для основного состояния квантовая теория и классическая механика дают принципиально разные ответы, что иллюстрирует рис.11.2.3. Зелёная линия на нём

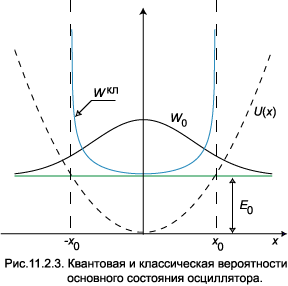
обозначает уровень нулевых колебаний E₀ из (1.10). Классическая вероятность увеличивается по мере приближения к точке x₀, определяемой условием U(x₀) = E₀, но не может перейти через эту границу. Квантовая теория предсказывает уменьшение вероятности при приближении к границе, причём частица может быть обнаружена в классически недоступной области x > x₀.

11.3. Нулевые колебания

В самом низком состоянии осциллятор имеет отличную от нуля энергию (1.10), определяемую его собственной частотой. Нулевые колебания осциллятора имеют чисто квантовую природу и находят своё объяснение в соотношении неопределённостей. Полная энергия осциллятора равна сумме кинетической и потенциальной

.

Если частица локализована внутри области размером x, то, согласно принципу Гайзенберга, её импульс не может быть меньше, чем

.

Таким образом, первое слагаемое в (3.1) уменьшается по мере увеличения x, а второе — растёт:

.

Полная энергия как функция x имеет минимум в точке

,

равный

.

Полученное значение в два раза отличается от результата точного расчёта. Это не удивительно, так как принцип неопределёности имеет характер оценки по порядку величины. Правильное выражение для энергии нулевых колебаний получается на основе формулы, содержащей точное неравенство для дисперсий момента и координаты:

.

Формально она выводится следующим образом. Пусть состояние частицы описывается функцией y(x), причём средние значения импульса и координаты для простоты вывода предполагаются равными нулю. Напишем очевидное неравенство

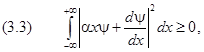
где a — действительная постоянная. Далее вычислим три полезных выражения:

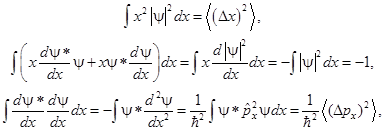
Они позволяют преобразовать левую часть (3.3) в квадратичный по a трёхчлен:

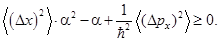
Этот трёхчлен не меняет знака ни при каких значениях a, если его дискриминант отрицателен, либо равен нулю. Отсюда вытекает условие

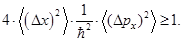
Легко видеть, что оно тождественно (3.2).

Плотность энергии нулевых колебаний

При выводе формулы Планка (2.4.7) мы представили спектральную плотность энергии излучения U_ω dω как произведение частоты мод колебаний dN_ω в единице объёма на среднюю энергию осциллятора <E>. Вычисление средней энергии выполнялось в рамках гипотезы Планка. Планк исходил из правила квантования осциллятора (2.4.1) – (2.4.3), не учитывающего нулевые колебания осциллятора. Повторим вычисления второй главы, заменив в определении средней энергии (2.4.4) выражение для энергии осциллятора E_n (2.4.1) – (2.4.3) на выведенное в этой главе правило квантования (1.9):

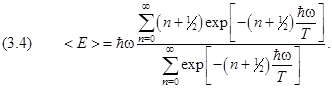
Сократим числитель и знаменатель на постоянный множитель :

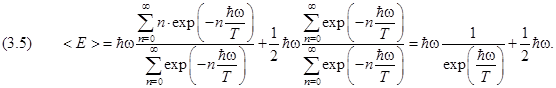
Первая сумма в правой части (3.5) уже была вычислена в разделе 2.2.4 второй главы, когда при расчёте средней энергии осциллятора из (2.4.4) мы получили (2.4.6). Вынесем за скобки множитель ћω и напишем окончательный результат:

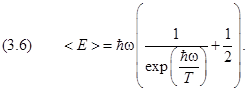
Его, конечно, можно было предвидеть: усреднение постоянной величины ћω, добавляемой к энергии (2.4.2), может дать только саму добавку.

Учёт нулевых колебаний приводит к переопределению чисел заполнения n_ω: вместо (2.4.7) теперь надо писать

Если Вам понравилась эта лекция, то понравится и эта - Воздействие территориальной организации населения на факторы промышленного производства.

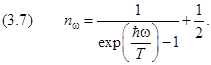
Подставляя среднюю энергию (3.6) и спектральную плотность числа осцилляторов (2.2.8) в (2.2.1), получим новое выражение для плотности энергии излучения чёрного тела с учётом нулевых колебаний:

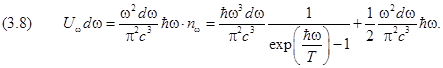
Последнее слагаемое в правой части и есть плотность энергии нулевых колебаний:

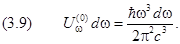
Нулевые колебания имеют хаотический характер и поэтому не дают вклада в вектор Умова–Пойнтинга. Попытка проинтегрировать формулу (3.9) по всему диапазону частот даёт расходящуюся величину. Такого рода расходимости часто возникают в квантовой электродинамике, и предложены различные рецепты их устранения. В вопросах, рассматриваемых в данном учебном пособии, положение спасает то обстоятельство, что нулевые колебания проявляются только во взаимодействии с другими физическими объектами. При этом всегда находится способ устранения расходимостей, поскольку интервал частот, участвующих во взаимодействии, ограничивается по естественным физическим причинам. Далее мы увидим, как это делается при решении задачи о сдвиге атомных уровней под влиянием нулевых колебаний — в задаче о лэмбовском сдвиге.