Связь квантовых и классических распределений Гиббса

2.7. Связь квантовых и классических распределений Гиббса

Для перехода от квантовых распределений к классическим распределениям надо заменить суммирование по всем возможным микросостояниям квантовой макроскопической системы интегрированием в многомерном фазовом пространстве. Чтобы осуществить такой переход надо определить элементарную ячейку в фазовом пространстве.

Рассмотрим движение одной частицы в потенциальном поле. Каждое состояние в этом случае характеризуется набором трех квантовых чисел: . При этом каждому состоянию в трехмерном фазовом пространстве отвечает объем , т.к. ввиду соотношения неопределенностей  точнее положение точки определить нельзя. Таким образом, на одну степень свободы приходится объем .

В квантовой теории показано, что в произвольной системе с N степенями свободы (при рассмотрении только поступательных степеней свободы) при переходе к классическому приближению в качестве элементарной ячейки надо использовать .

Поэтому заменим суммирование по квантовым числам интегрированием по фазовому пространству:  (движение атома как целого).

Штрих означает, что интегрирование проводится не по всему фазовому пространству, а лишь по тем его областям, которые соответствуют физически различимым состояниям.

В классической системе одинаковых частиц они считаются различимыми, то есть их можно перенумеровать и проследить за их траекториями. В квантовой механике показано, что частицы являются тождественными (неразличимыми), а проследить за траекториями частиц невозможно. То есть если рассмотреть возможные варианты распределения, например, трех частиц по трем ячейкам, то в классической механике состояния, отвечающие разным номерам частиц, считаются разными, а в квантовой механике все они представляют собой одно состояние.

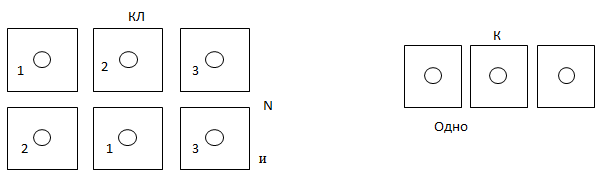
Рис.2.1

Рекомендуемые материалы

При вычислении статистического интеграла удобно распространить интегрирование на всю область фазового пространства. При этом состояния, отличающиеся лишь перестановкой частиц (неразличимых в квантовой механике) будут учитываться N! раз. Поэтому разделим статистический интеграл на N!. Это означает, что условием перехода к классической статистической теории будет замена:

,

а статистическая сумма примет вид

.

Заметим, что это выражение безразмерно (в отличие от ранее полученного в классической статистической физике).

Тогда можно ввести безразмерную функцию распределения в классической теории

.

Ещё посмотрите лекцию "Формирование в подсознании потребителя эффективного рекламного образа товара" по этой теме.

Условие её нормировки: .

Во многих случаях (например, для нахождения уравнений состояний) это различие на  не является существенным. Однако, при расчете энтропии оно оказывается принципиальным.

Решение парадокса Гиббса.

Воспользуемся формулой Стирлинга для больших величин N:

 .

При подстановке этого выражения в энтропии газов, получим, что парадокса Гиббса не возникает. То есть учет тождественности частиц в квантовой теории позволяет устранить противоречия в классических выражениях для термодинамических функций. Таким же образом можно найти и все остальные термодинамические функции.