Вращательное движение. Равномерное движение точки по окружности. Вектор угловой скорости

Вращательное движение. Равномерное движение точки по окружности. Вектор угловой скорости. Угловое ускорение. Связь угловых и линейных величин

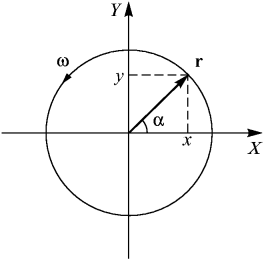
При равноускоренном движении частица движется все время в одной плоскости, образуемой начальным вектором скорости и постоянным ускорением a. Однако очевидно, что далеко не всякое плоское движение является равноускоренным. Пример плоского неравноускоренного движения, известный вам из школьного курса физики, — это равномерное движение по окружности. Давайте рассмотрим его здесь. Поскольку это движение плоское, выберем в качестве этой плоскости, плоскость XY. Начало координат выберем в центре окружности (pис. 1).

Координаты частицы выразим через величину радиуса окружности r и угол :

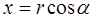
                                                                                            (1)

Поскольку движение происходит по окружности, r от времени не зависит. Функцией времени является только угол . Производная от угла по времени называется угловой скоростью вращения :

                                                                                                 (2)

Рекомендуемые материалы

При равномерном вращении по окружности  и можно проинтегрировать это уравнение. В результате

                                                                                          (3)

Константа интегрирования выбирается из условия. Таким образом,

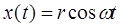
                                                                                           (4)

Это полностью определяет движение. Так, скорость материальной точки определяется производными по времени от координат:

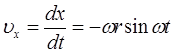
                                                                                 (5)

Скалярное произведение pавно

           (6)

что означает перпендикулярность векторов r и , то есть скорость действительно направлена по касательной к окружности. Абсолютная величина скорости равна

           (7)

она не зависит от времени, движение действительно равномерное (но по окружности).

Дифференцируя по времени скорость, мы можем определить ускорение:

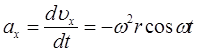
                                                                           (8)

откуда следует, что ускорение зависит от времени, то есть движение не является равноускоренным. Абсолютная величина ускорения (модуль), тем не менее, остается постоянной:

                                                                         (9)

или, так как, то мы получаем

                                                                                                   (10)

— известную из школьного курса физики формулу для центростремительного ускорения. Почему центростремительного? Да потому, что вектор a направлен к центру. В этом нетрудно убедиться, подсчитав скалярное произведение:

                                                                                                                     (11)

С другой стороны,

                                                 (12)

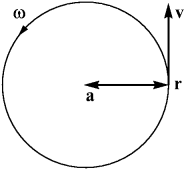
Из сравнения двух этих выражений получаем, что . Таким образом, вектор ускорения антипараллелен вектору r, то есть направлен к центру. В результате картина направлений векторов выглядит, как показано на рис. 2.

До сих пор при рассмотрении вращательного движения мы оперировали проекциями векторов на оси координат. Между тем, часто бывает полезно иметь соотношения, не зависящие от выбора системы координат, или, как говорят, записанные в векторной форме. Примером таких соотношений является выражение для координаты и скорости частицы при равноускоренном движении.

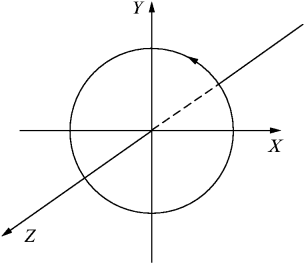
При рассмотрении вращательного движения мы ввели угловую скорость вращения  как производную по времени от угла поворота : . Давайте теперь зададимся вопросом, какой величиной, скалярной или векторной, является угол поворота. Ведь когда говорят о повороте, нужно указывать не только величину угла поворота, но и то, вокруг какой оси происходит вращение (поворот) и в какую сторону (по часовой стрелке или против). В разобранном выше примере осью вращения была ось z и, поскольку мы использовали правую систему координат, вращение происходило по часовой стрелке (если смотреть в положительном направлении вдоль оси z) (pис. 3).

С этой точки зрения угол поворота должен быть величиной векторной. Однако, как мы убедимся на следующей лекции, произвольный угол поворота вектором, вообще говоpя, не является. Понятие вектора применимо лишь по отношению к бесконечно малым углам поворота.

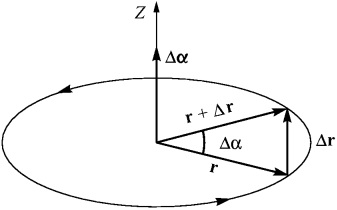
Поэтому, говоря о повороте на какой-то малый угол , можно приближенно говорить о векторе , величина которого равна углу поворота, а направление показывает направление оси вращения так, чтобы поворот происходил по часовой стрелке, или в соответствии с правилом буравчика. В нашем конкретном случае вектор коллинеарен с направлением оси z. Зададимся вопросом, как связано перемещение материальной точки  при повороте ее радиус-вектора r на малый угол  (pис. 4).

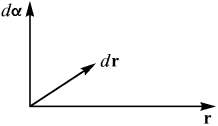
На этот вопрос легко ответить, если речь идет о бесконечно малых поворотах . Тогда бесконечно малым является и перемещение dr. Его величина (равная длине хорды) совпадает теперь с длиной дуги, то есть

                                                                                                 (13)

а по направлению вектор dr совпадает с касательной, то есть перпендикулярен r. В результате мы имеем три взаимно перпендикулярные вектора r, dr и , образующие правую тройку (pис. 5),

Причем . Те, кто помнят из школьного курса о векторном произведении векторов, без труда сообразят, что искомое соотношение можно записать в виде векторного равенства

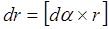                                                                                           (14)

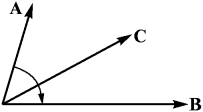
Действительно, по определению, векторным произведением двух векторов  называется вектор

                                                                                           (15)

который направлен перпендикулярно плоскости, в которой лежат (или которую образуют) два вектора A и B, в сторону от этой плоскости, соответствующую правилу буравчика (см. рис. 6).

Величина же вектора C равна произведению модулей векторов на синус угла между ними:

                                                                                       (16)

В нашем случае угол между векторами  и r равен 90^°, так что синус равен единице. А поскольку, как мы уже писали, 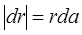, то мы убеждаемся в справедливости векторного соотношения .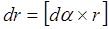

Разделив обе стороны этого равенства на бесконечно малый временной интервал dt, в течение которого произошло изменение вектора r на dr, мы получим

                                                                                       (17)

Но величина, стоящая в левой части равенства, есть не что иное, как скорость частицы , а производная

                                                                                                  (18)

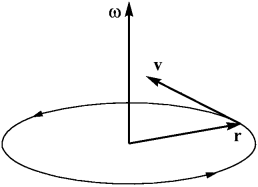
называется вектором угловой скорости. Ее мы вначале ввели по абсолютной величине, а теперь показали, что имеет смысл говорить об угловой скорости вращения как о векторе. Ее величина определяет величину угловой скорости (скорость вращения, или скорость изменения угла), а направление параллельно оси вращения, причем так, что имеет место правило буравчика. Итак, мы получили, что

                                                                                                                (19)

Оpиентация этих тpех вектоpов показана на pис. 7.

Чтобы получить ускорение a, надо от обеих частей взять производную по времени. Если  постоянно (как по величине, так и по направлению), то

                                                                          (20)

то есть ускорение оказывается перпендикулярным угловой скорости вращения  и скорости движения . А поскольку последняя направлена по касательной, то, значит, ускорение направлено либо параллельно r, либо антипараллельно. Как именно, можно выяснить, подставив в вышеприведенную формулу значение :

           (21)

Поскольку в рассматриваемом нами примере начало кооpдинат выбpано в центpе окpужности, то угловая скорость  и радиус-вектор r перпендикулярны друг другу а, следовательно, их скалярное произведение равно нулю (вообще говоря, как мы сейчас увидим, далеко не всегда ) и мы получаем

                                                                                                (22)

то есть антипараллельность векторов a и r (вспомните термин «центростремительное ускорение»). По величине они таковы: , то есть имеем уже знакомый результат.

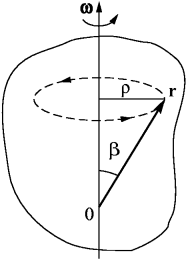
Записанные нами соотношения справедливы и в более общем случае, когда мы рассматриваем вращение системы материальных точек или твердого тела как целого (pис. 8).

Имея в виду эту картину, нетрудно показать, что здесь, хотя  и r не перпендикулярны друг другу, тем не менее, выполняется прежнее соотношение для скорости движения некоторой выбранной нами точки с радиус-вектором r:

                                                                                              (23)

Действительно, как следует из рис. 8, точка движется по окружности радиуса  со скоростью . Но поскольку — это угол между векторами  и r, мы убеждаемся в справедливости этой формулы.

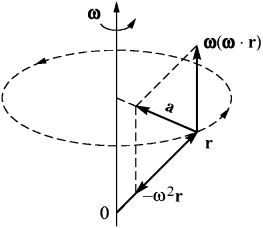
Теперь нам понятно происхождение дополнительного слагаемого в центростремительном ускорении (см. pис. 9):

                                                                                            (24)

Таким образом, ускорение a на самом деле направлено не к центру, а к оси вpащения, поэтому его можно было бы называть осестремительным. Но, pазумеется, дело не в названиях.

В пользу соотношения  говорит и то, что оно справедливо в более общем случае, когда вектор угловой скорости  не является постоянным и зависит от времени: . Тогда формула для ускорения изменится — в ней появится дополнительное слагаемое:

                                (25)

Величина  называется угловым ускорением. Оно появляется, если меняется по величине угловая скорость (замедляется, например, вращение вокруг фиксированной оси) либо поворачивается с течением времени сама ось вращения (либо и то и другое).

В заключение для справок приведем выражение для декартовых компонент векторного призведения :

,       

,       

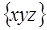
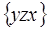
,                                                                (26)

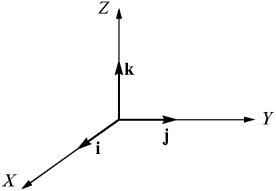
Здесь для запоминания следует использовать указанные выше циклические перестановки. Эти соотношения легко доказываются, если записать каждый вектор в виде

                                                                              (27)

и, аналогично, вектор B. Затем следует учесть, что векторные призведения единичных ортов i, j и k между собой равны соответственно (см. pис. 10)

Ещё посмотрите лекцию "10.11 Основные богословско-юридические школы ислама" по этой теме.

,                    ,                                                           (28)

и что при изменении порядка сомножителей изменяется знак векторного произведения:

 и т. д.                                                                            (29)

Далее нужно произвести векторное умножение

                                  (30)

воспользовавшись приведенными выше правилами.