Определение внутренних усилий при изгибе

6.2 Определение внутренних усилий при изгибе

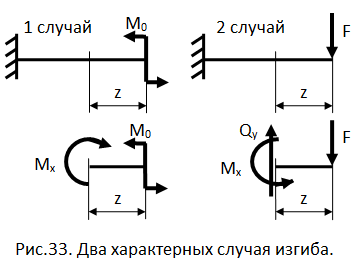
Рассмотрим два характерных случая изгиба: в первом - консольная балка изгибается  сосредоточенным  моментом М₀; во втором - сосредоточенной силой F.

Мысленно рассекая стер-жень сечением, перпенди-кулярным продольной оси и составляя уравнения равно-весия для отсеченных час-тей балки, определим внут-ренние усилия в том и другом случае:

1 случай:  

 : ;   (6.1)

:  (6.2)

2 случай:

 ;     (6.3)

   (6.4)

Рекомендуемые материалы

Остальные уравнения равновесия, очевидно, тождественно равны нулю.

Таким образом, в общем случае плоского изгиба в сечении балки из шести внутренних усилий возникает два - изгибающий момент М_z и поперечная сила Q_y (или при изгибе относительно другой главной оси - изгибающий момент M_y и поперечная сила Q_x).

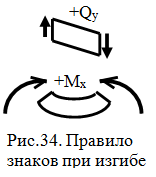
При определении внутренних усилий будем придерживаться следующего правила знаков:

Информация в лекции "Команды ОС для компиляции" поможет Вам.

- поперечная сила считается положительной, если она стремится повернуть рассматриваемый элемент балки по часовой стрелке;

- изгибающий момент считается положительным, если при изгибе элемента балки верхние волокна элемента оказываются сжатыми, а нижние - растянутыми.

Таким образом, решение задачи по определению внутренних усилий при изгибе будем выстраивать по следующему плану:

1) на первом этапе, рассматривая условия равновесия конструкции в целом, определяем, если это необходимо, неизвестные реакции опор (отме­тим, что для консольной балки реакции в заделке можно и не находить, если рассматри­вать балку со свободной стороны;

2) на втором этапе выделяем характерные участки балки,
принимая за границы участков точки приложения сил, точки изменения формы или размеров балки; 3) на третьем этапе в сечениях балки, рассматривая условия равновесия элементов балки на каждом из участ­ков определяем внутренние усилия.