Малые свободные колебания системы

Малые свободные колебания системы.

Свободными колебаниями называется колебательное движение системы, выведенной из положения равновесия и предоставленной самой себе.

Составим уравнение Лагранжа для консервативной системы:

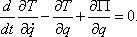
Используя (4) и (5), получим дифференциальное уравнение свободных колебаний или, обозначив

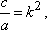
(6)

Решение этого однородного линейного дифференциального уравнения второго порядка с постоянными коэффициентами известно:

(7)

или, использовав другие постоянные и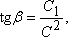

Рекомендуемые материалы

(8)

Следовательно, малые свободные колебания – гармонические колебания, причем амплитуда колебаний и начальная фаза определяются начальными условиями (q и при t = 0), а частота колебаний k и период Т не зависят от начальных условий, определяются только конструкцией системы.

Обычно частоту колебаний находят сравнением полученного дифференциального уравнения с уравнением (6).

Пример 27. Тело весом Р подвешено на нити, перекинутой через блок и прикрепленной к пружине (рис.82). Вес блока G, радиус - r; жесткость пружины с. Определим период свободных колебаний системы.

Рис.82

Назначим обобщенной координатой смещение z груза по вертикали от положения равновесия, при котором пружина была растянута на величину .

Тогда потенциальная энергия относительно положения равновесия Где - полная деформация пружины, а - потенциальная энергия пружины в положении равновесия, которую вычитаем из потенциальной энергии полностью деформированной пружины. Раскрыв скобки, получим

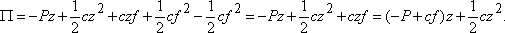
В положении равновесия должно выполняться условие . Отсюда значит,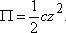

Кинетическая энергия системы

Вместе с этой лекцией читают "8 Вывод на знаниях".

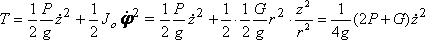
Составив уравнение Лагранжа, получим или Сравнивая с (6), находим частоту колебаний и затем период

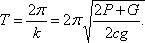
Пример 28. Определим период малых колебаний балочки АВ на цилиндрической поверхности (см. пример 26).

Потенциальная и кинетическая энергии определены. Разложим их в ряд с точностью до малых величин второго порядка. Для этого достаточно положить а Получим Кинетическая энергия получится такой (отбросив член четвертого порядка - ):

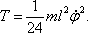
Составляем уравнение Лагранжа. Определив производные

получим уравнение Приводим его к форме (6): Поэтому частота малых колебаний и период