Свободные колебания системы с учетом сил сопротивления движению

Свободные колебания системы с учетом сил сопротивления движению.

Известно, что свободные колебания не длятся очень долго. Как правило они, как говорят, затухают и довольно скоро. Причиной этому является чаще всего – сопротивление среды, в которой движутся части колебательной системы.

Обычно считают это сопротивление пропорциональным скорости. Пусть на каждую точку материальной системы действует сила сопротивления Обобщенная сила, соответствующая этим силам,

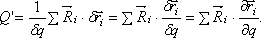
Скорость точек так как - сложная функция, а Поэтому Значит,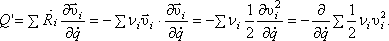

Обозначим Тогда обобщенная сила сопротивления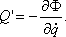

Заметим, что по форме эта функция аналогична кинетической энергии Т. Поэтому, если разложить ее в ряд Маклорена и учесть члены лишь второго порядка малости, результат получится тоже аналогичным (5): (коэффициент b также будет положительным). И тогда обобщенная сила сопротивления движению

(9)

Функция называется диссипативной или функцией рассеивания энергии системы.

Рекомендуемые материалы

После подстановки в уравнение Лагранжа , получим дифференциальное уравнение или

(10)

где - коэффициент сопротивления, - частота свободных колебаний без сопротивления.

Найдем решение уравнения (10). Характеристическое уравнение: Корни его могут быть и комплексными, и вещественными в зависимости от сопротивления, от величины коэффициента n.

а) Случай малого сопротивления (n < k).

Корни получаются комплексными где 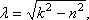. Решение дифференциального уравнения ищем в виде

(11)

или

(12)

где постоянные и или и находятся по начальным условиям.

Сравнивая решение (12) с (2), делаем вывод, что это будут колебания, но не гармонические, так как амплитуда колебаний, равная , не постоянная, уменьшается с течением времени. Поэтому такие колебания и называются затухающими.

График таких колебаний дан на рис. 83.

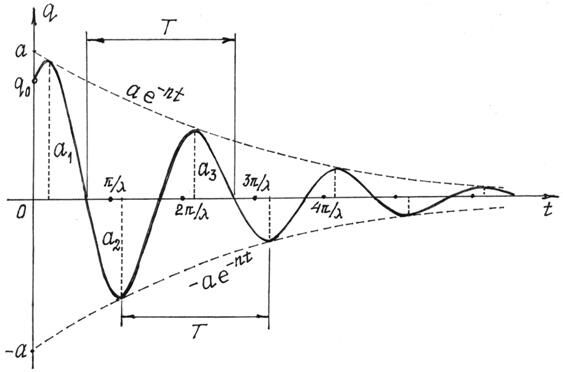
Рис.83

Следует заметить, что колебательный процесс не будет периодическим. Но, так как система проходит через положение равновесия через равное время, все-таки вводят понятие периода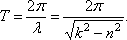

Если сравнить этот период колебаний с периодом колебаний системы без сопротивления (3), увидим, что сопротивление увеличивает период колебаний и уменьшает их частоту.

Интересна закономерность изменения амплитуды. Найдем отношение соседних амплитуд (через полпериода ):

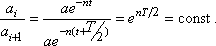
То есть амплитуды уменьшаются по закону геометрической прогрессии, знаменателем которой является величина .

Натуральный логарифм ее, равный называется логарифмическим декрементом колебаний.

Конечно, через период амплитуда уменьшится в раз, а через m периодов – в раз.

б) Случай большого сопротивления (n>k).

Корни характеристического уравнения получатся вещественными: В этом случае, как известно из курса математики, решение дифференциального уравнения (10):

(13)

Решение явно неколебательное, непериодическое.

Графики таких движений показаны на рис.84. Вид движения зависит от начальных условий и величины коэффициента сопротивления n.

"Основные черты развития Византийской империи" - тут тоже много полезного для Вас.

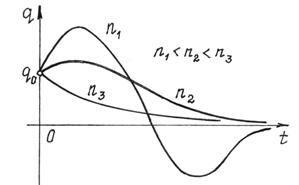
Рис.84

в) Случай равного сопротивления (n = k).

Корни характеристического уравнения получаются равными: . Поэтому решение дифференциального уравнения

(14)

Движение и в этом случае не будет колебательным.