Условная энтропия, сжатие классических данных, двоичный симметричный канал связи, коды, исправляющие ошибки
Лекция 3.
1. Условная энтропия. Взаимная информация. Канал связи.
2. Сжатие классических данных. Типичные слова. Теорема Шеннона для незашумленного канала связи.
3. Двоичный симметричный канал связи. Емкость канала.
4. Коды, исправляющие ошибки. Код Хамминга. Теорема Шеннона для зашумленного канала.
Обратимые логические операции. Универсальные ЛЭ Тоффоли и Фредкина.
(Из прошлой лекции - не успел)
Связь энтропии и информации.
Итак, информационная энтропия - это мера недостатка (или степень неопределенности) информации о действительном состоянии физической системы.
Рекомендуемые материалы
Информационная энтропия Шеннона:
 , где
, где  (1)
(1)
(это относится к двухуровневым системам, типа бит: “0” и “1”. Если размерность равна n, то H = lognDG. Так, для n = 3, Н = log3DG, причем, DG = 3.)
В идеальном случае, когда отсутствуют шумы и помехи, создаваемые внешними источниками в канале связи, конечное распределение вероятностей после измерения сводится к одному определенному значению pn = 1, т.е. H = 0, а максимальное значение полученной при измерении информации будет определяться : Imax = H0. Таким образом, информационная энтропия Шеннона системы имеет смысл максимальной информации, заключенной в системе; она может быть определена в идеальных условиях измерения состояния системы в отсутствие шумов и помех, когда энтропия конечного состояния равна нулю:
H = 0.
Часто величину (1) называют информационным содержанием
Пусть Х - случайная величина, принимающая значения X = {x1,x2...xn}, а p(x) - ее функция распределения. Тогда информационное содержание или информационная энтропия величины Х:
 . (2)
. (2)
Рассмотрим три примера.
Пример 1. Если мы знаем, что Х = 2, то p(2) = 1 и в сумме (2) нет других слагаемых, то H = 0, т.е. информационное содержание величины Х равно нулю.
Пример 2. Если величина Х получается при подбрасывании кости с равновероятным распределением p(x) = 1/6 для x Î {1, 2, 3, 4, 5, 6}. Тогда  Если Х может принимать N различных значений, то информационное содержание величины Х максимально, когда распределение вероятностей равномерное, т.е. p(x) = 1/N. Таким образом, для честной кости Н @ 2.58, а для нечестной, когда, например, p(6) = 1/2, P(1, 2,...5) = 1/10 получаем Н = 2.16. Это утверждение можно строго доказать. Заметим, что оно сочетается с нашим пониманием физического смысла энтропии в том смысле, что информационное содержание (энтропия) максимально, если априорное знание об Х минимально. Это свойство используется, например, в криптографии, где необходимо выбирать (неортогональные) базисы равновероятным образом.
Если Х может принимать N различных значений, то информационное содержание величины Х максимально, когда распределение вероятностей равномерное, т.е. p(x) = 1/N. Таким образом, для честной кости Н @ 2.58, а для нечестной, когда, например, p(6) = 1/2, P(1, 2,...5) = 1/10 получаем Н = 2.16. Это утверждение можно строго доказать. Заметим, что оно сочетается с нашим пониманием физического смысла энтропии в том смысле, что информационное содержание (энтропия) максимально, если априорное знание об Х минимально. Это свойство используется, например, в криптографии, где необходимо выбирать (неортогональные) базисы равновероятным образом.
Пример 3. Какое количество информации содержится в утверждении: “зимой холодно”? С одной стороны для жителей России в этом сообщении не содержится ничего нового - информация равна нулю. Однако, рассмотрим его с информационной точки зрения. Закодируем буквы русского алфавита (32 штуки с пробелом, без “ё”и без “й”) с помощью символов  . Например, с помощью таблицы:
. Например, с помощью таблицы:
| а | б | в | г | д | е | ж | з | и | к | л | м | н | о | п | р | с |
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | x11 | x12 | x13 | x14 | x15 | x16 | x17 |
| т | у | ф | х | ц | ч | ш | щ | ъ | ы | ь | э | ю | я | _ |
| x18 | x19 | x20 | x21 | x22 | x23 | x24 | x25 | x26 | x27 | x28 | x29 | x30 | x31 | x32 |
Тогда наше сообщение принимает вид
 (*)
(*)
Длина последовательности символов  равна 13. Буква “о” (
равна 13. Буква “о” ( ) встречается 4 раза, поэтому
) встречается 4 раза, поэтому  . Будем рассматривать последовательность (*) как функцию
. Будем рассматривать последовательность (*) как функцию  случайной величин, где
случайной величин, где  принимает 32 значения с некоторыми вероятностями
принимает 32 значения с некоторыми вероятностями  . (Здесь ошибка - буква “и” встречается два раза!)
. (Здесь ошибка - буква “и” встречается два раза!)
Таким образом если в некотором сообщении, состоящем из n букв алфавита, содержащего N символов заданы вероятности  найти ту или иную букву
найти ту или иную букву  , то количество информации вычисляется как произведение число букв n на информацию, содержащуюся в одной букве S(X):
, то количество информации вычисляется как произведение число букв n на информацию, содержащуюся в одной букве S(X):
 .
.
В нашем примере n = 13,  , поэтому
, поэтому
 .
.
Если бы мы взяли равновероятное распределение для появления буквы по всему алфавиту  (что, конечно, не так!), то получили:
(что, конечно, не так!), то получили:
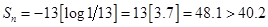
Заметим, что приведенный пример не вполне корректен. Мы использовали вероятность встретить ту или иную букву в коротком сообщении для малого числа n букв. На самом деле, необходимо брать длинные сообщения и использовать вероятности  , характерные для всего русского языка.
, характерные для всего русского языка.
Максимальная информация, которая может быть, в принципе, запасена в переменной, принимающей N различных значений, составляет  и достигается при равномерном распределении вероятностей. Выбор основания “2” у логарифма в теории информации обусловлен требованием Н(Х) = 1, когда Х может принимать два значения с одинаковой вероятностью (N = 2). Двухуровневые переменные, таким образом, содержат единицу информации - бит, а величина Х, принимающая два значения, называется бинарной.
и достигается при равномерном распределении вероятностей. Выбор основания “2” у логарифма в теории информации обусловлен требованием Н(Х) = 1, когда Х может принимать два значения с одинаковой вероятностью (N = 2). Двухуровневые переменные, таким образом, содержат единицу информации - бит, а величина Х, принимающая два значения, называется бинарной.
Пусть для двухуровневой переменной Х, вероятность того, что Х = 1, равна р, а вероятность того, что Х = 0 равна 1 - р. Тогда информационная энтропия есть функция только р:
 (3)
(3)
Далее в этой лекции под Н(р) понимается именно энтропия бинарных сигналов.
Условная энтропия.
Рассмотрим условную вероятность p(y|x) - вероятность того, что величина Y принимает значение y при условии, что величина Х принимает значение х. Условной энтропией называется величина S(Y|X):
 (4)
(4)
где во втором равенстве использовано понятие совместной вероятности
 - есть вероятность того, что Х принимает значение х, а Y принимает значение y. Также использовалось правило усреднения совместного распределения по лишним “переменным”:
- есть вероятность того, что Х принимает значение х, а Y принимает значение y. Также использовалось правило усреднения совместного распределения по лишним “переменным”:  . Аналогично можно показать, что
. Аналогично можно показать, что  . Кроме того, мы ввели энтропию совместного распределения:
. Кроме того, мы ввели энтропию совместного распределения:
 , (4а)
, (4а)
Из определения (4) следует, что S(Y|X) есть мера того, сколько информации, в среднем, оставалось бы в Y при условии, что мы бы знали Х. Заметим, что всегда S(Y|X) £ S(Y) и обычно S(Y|X) ¹ S(Х|У).
Понятие условной энтропии служит краеугольным камнем для другой величины - взаимной информации, определяемой как
 . (5)
. (5)
По определению величина I(X:Y) есть мера того сколько информации содержат Х и Y друг о друге. Например, если Х и Y - независимые величины, то p(x,y) = p(x)p(y), так что I(X:Y) = 0. Соотношения между основными мерами классической информации показаны на рисунке.
Можно показать, что S(X,Y) - информационное содержание величин Х и У (информация, которую мы бы получили, если бы не зная ничего изначально, мы бы узнали значения Х и Y) удовлетворяет
 :
:
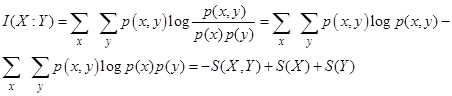
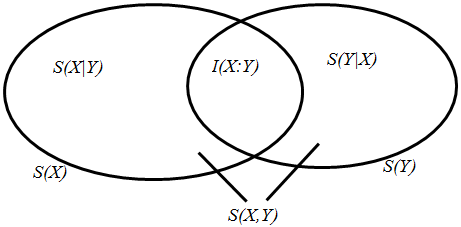
Информация может исчезнуть, но она не может возникнуть из ничего. Этот важный факт отражается в математической формулировке “неравенства получения данных”:
 . (6)
. (6)
Символы со стрелками означают, что величины X, Y, Z, составляют марковский процесс, в котором Z зависит от У, и не зависит непосредственно от Х:
 .
.
Содержание “неравенства получения данных” состоит в том, что “data processor” Y может передать к Z информации не больше, чем он получил от Х.
Сжатие данных (data compression)
Как доказать, что определение (1) служит хорошей мерой информации? На первый взгляд кажется непонятно, как разрешить эту задачу. Рассмотрим следующую простую ситуацию (см. рисунок).

Пусть некая персона Х (традиционно ее зовут Алиса) хочет передать сообщение приятелю (его зовут Бобом). Ограничим себя только случаем, когда Х имеет только два значения: “нет” и “да”. Мы говорим, что Алиса служит “источником” с “алфавитом” из двух символов. Алиса общается с Бобом посредством пересылки битов (нулей и единиц). Между Алисой и Бобом размещается “канал связи” - физическая система, передающая или преобразующая информацию. В качестве канала связи может выступать и логическое устройство.
Если Х - дискретная случайная величина, принимающая значения на множестве  . Рассмотрим случайный источник (Алиса), который порождает последовательность независимых одинаково распределенных случайных величин с распределением p. Последовательность
. Рассмотрим случайный источник (Алиса), который порождает последовательность независимых одинаково распределенных случайных величин с распределением p. Последовательность  {всего n штук} букв алфавита K называется словом длины n. Общее число таких слов
{всего n штук} букв алфавита K называется словом длины n. Общее число таких слов  . Например, K= {1, 2, 3}. Пусть n = 2. Сколько всего слов, составленных из n = 2 символов 1, 2, 3? Очевидно их 32 = 9 штук. Общее же число слов, составленных из n букв (символов) есть:
. Например, K= {1, 2, 3}. Пусть n = 2. Сколько всего слов, составленных из n = 2 символов 1, 2, 3? Очевидно их 32 = 9 штук. Общее же число слов, составленных из n букв (символов) есть:
 .
.
Значит, чтобы закодировать все эти слова, используя двоичные последовательности, казалось бы что потребуется  бит! (Если
бит! (Если  - нужно n бит информации).
- нужно n бит информации).
Однако есть лучший способ кодирования - сжатие данных - который использует то обстоятельство, что распределение p - неравномерная величина.
Будем измерять информационное содержание Х, подсчитывая в среднем число битов, которое должна послать Алиса, для того чтобы Боб распознал Х. Очевидно, она должна просто посылать “0” как “нет и “1” как “да”, обеспечивая “скорость битов” в один бит на Х. Однако, что будет, если Х является существенно случайной переменной, исключая случаи, когда нули идут чаще, чем единицы? Оказывается, что в этом случае Алиса может передавать сообщения Бобу более эффективно, используя следующую процедуру.
Пусть р - вероятность того, что Х = 1 и 1 - р - вероятность того, что Х = 0. Алиса ждет, пока n значений Х будут готовы для того, чтобы их переслать (n - большое число). Среднее число единиц в такой последовательности n значений равно np. Это - наиболее вероятное число единиц в любой последовательности, которая содержит n символов, так что число единиц будет всегда близко к np. Пусть np - целое число. Найдем вероятность получения любой последовательности, содержащей np единиц. Это будет произведение того, что в последовательности есть np единиц (pnp) и того, что остальные элементы - n(1-p) нули {(1-p)n(1-p)} - итого, np + n - np = n
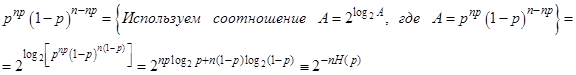
где Н(р) - определена в (3) для двоичной кодировки. Такая последовательность называется типичной последовательностью или типичным словом. Более точно, определим типичное слово как последовательность, которая удовлетворяет условию
 ,
,
где р(слово) - вероятность появления последовательности (слова) Т.е. типичная последовательность содержит наиболее вероятное число единиц (нулей).
Теперь можно показать, что вероятность образования типичной последовательности из n величин Алисы превосходит величину 1-e для достаточно больших n, вне зависимости от того, насколько мало e! Это означает, что Алисе не нужно передавать n бит Бобу для того, что бы он распознал n исходов. Ей лишь нужно сказать Бобу какова ее типичная последовательность. Им нужно договориться заранее о том, как выделять (в смысле отмечать) эти типичные последовательности. Например, они могут нумеровать их в порядке увеличения бинарного значения. Алиса просто посылает свое обозначение (метку), но не саму последовательность.
Чтобы проследить, насколько хорошо работает этот метод можно показать, что все типичные последовательности имеют одинаковые вероятности и, следовательно, их существует  штук. Для передачи одной из
штук. Для передачи одной из  последовательностей, очевидно, Алиса должна послать nH(p) бит. Ясно, что Алиса не может сделать ничего лучше этого (т.е. послать меньшее число бит) т.к. типичные последовательности равновероятны: никакой информации не может быть извлечено при дальнейших манипуляциях. Поэтому информационное содержание или информационная энтропия каждого значения из множества Х в оригинальной последовательности должно быть H(p), что доказывает справедливость (2)!
последовательностей, очевидно, Алиса должна послать nH(p) бит. Ясно, что Алиса не может сделать ничего лучше этого (т.е. послать меньшее число бит) т.к. типичные последовательности равновероятны: никакой информации не может быть извлечено при дальнейших манипуляциях. Поэтому информационное содержание или информационная энтропия каждого значения из множества Х в оригинальной последовательности должно быть H(p), что доказывает справедливость (2)!
Мы не вдаемся в математические детали доказательства. Отметим, лишь, что использован закон больших чисел, который гласит, что для произвольно малых e и d выполняется неравенство
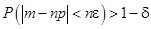
для достаточно больших n, где m - число единиц, содержащихся в последовательности длиной n. Для достаточно больших n число единиц m будет отличаться от среднего значения np на число как угодно малое по сравнению с n. Например, в рассмотренном выше случае нули и единицы будут распределены по биномиальному закону
 ,
,
где распределение Гаусса получается в пределе, когда n, np ® ¥, стандартное отклонение  , а
, а  - число сочетаний из n по m.
- число сочетаний из n по m.
Все эти соображения, относящиеся к определению информационной энтропии (информационному содержанию) (2) имеют важное практическое значение. Оно состоит в том, что для передачи n значений величины Х (определена на множестве {0, 1}) нам нужно послать через канал связи только nH(X) £ n бит.
Этот алгоритм получил название классического сжатия данных или теоремы Шеннона для нешумящего канала связи.
Пример. Пусть p = 1/4. Тогда по теореме Шеннона лучшее из того, что дает техника сжатия данных это передача каждого сообщения из четырех значений Х посылкой в среднем 4Н(1/4) ~ 3.245 бит.
Техника сжатия данных нашла огромное применение в телекоммуникации. Например, при сжатии информации для передачи телевизионных изображений и сохранении их в памяти компьютера. С точки зрения инженерного дизайна канала связи сжатие данных может показаться фантастической техникой. Предположим у нас есть телефонная связь с гористой местностью, но скорость связи не очень высока для того, чтобы послать, скажем, видео-изображение. Обычное инженерное решение состоит в замене телефонной линии на более быструю, в то время как из теории информации следует, что можно использовать старую линию, но при условии (де)компрессии данных на одном из двух концов (компрессия на одном и декомпрессия на другом конце). Удивительно, что пригодность кабеля может быть улучшена “починкой” информации, а не самого кабеля.
Двоичный симметричный канал связи
До сих пор мы рассматривали случаи идеальной передачи сообщений посредством нешумящих каналов. Теорема Шеннона дает нам меру лучшей компрессии данных в условиях идеальной связи.
Теперь остановимся на случае передачи информации при наличии шума в канале. рассмотрим лишь простейшие случаи.
Предположим, что у нас имеется двоичный канал связи, т.е. когда Алиса посылает Бобу только нули и единицы. Нешумящий канал передает значения по схеме  . Зашумленный канал иногда выдает нуль вместо единицы и наоборот.
. Зашумленный канал иногда выдает нуль вместо единицы и наоборот.
Существует большое число разновидностей шума. Например, “инверсия бита” приводит к равновероятному перевороту бита  . Иногда канал имеет тенденцию к релаксации, т.е.
. Иногда канал имеет тенденцию к релаксации, т.е.  , в то время как обратный процесс
, в то время как обратный процесс  невозможен. Возможны случаи, когда такие процессы идут случайно от бита к биту или возникают и кончаются внезапно.
невозможен. Возможны случаи, когда такие процессы идут случайно от бита к биту или возникают и кончаются внезапно.
Очень важную разновидность шума представляет собой процесс, при котором воздействие на биты происходит независимо и ошибки возникают по схеме  . Эти ошибки наиболее близки к реальным шумовым процессам. Если две ошибки
. Эти ошибки наиболее близки к реальным шумовым процессам. Если две ошибки  равновероятны, то канал связи называется двоичным симметричным каналом. Такой канал характеризуется единственным параметром р, который есть просто вероятность ошибки на один посланный бит. Предположим, что Алиса посылает в канал сообщение Х, а Боб получает зашумленное сообщение Y. Задача Боба состоит в оптимальном извлечении Х из Y. Если Х состоит из единственного бита, то Боб может использовать условные вероятности:
равновероятны, то канал связи называется двоичным симметричным каналом. Такой канал характеризуется единственным параметром р, который есть просто вероятность ошибки на один посланный бит. Предположим, что Алиса посылает в канал сообщение Х, а Боб получает зашумленное сообщение Y. Задача Боба состоит в оптимальном извлечении Х из Y. Если Х состоит из единственного бита, то Боб может использовать условные вероятности:
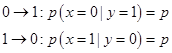
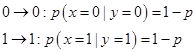
из которых можно найти S(X|Y) используя (3, 4):
 (рассматриваем случай, когда вероятность появления нулей и единиц совпадает:
(рассматриваем случай, когда вероятность появления нулей и единиц совпадает: ) =
) = 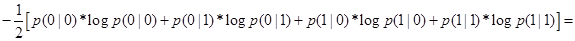
 = H(p). Тогда из определения (5) взаимной информации получаем:
= H(p). Тогда из определения (5) взаимной информации получаем:
 . (7)
. (7)
Очевидно, что наличие шума в канале ограничивает информацию об Алисиной величине Х, содержащейся в принятом Бобом сигнале Y. Кроме того из неравенства сжатия данных (6) Боб не может увеличить информацию об Х манипулируя Y. Однако из (7) следует, что качество связи между Алисой и Бобом может улучшаться при росте S(X). Оказывается, что информация зависит как от свойств источника, так и от свойств канала. Было бы полезно ввести некую меру, характеризующую только канал связи для того чтобы знать насколько хорошо канал передает информацию. Такая величина называется емкостью канала связи. Она определяется как максимальная взаимная информация I(X:Y) между входом и выходом, причем максимизация происходит по всем возможным источникам шума:
Емкость канала  (8)
(8)
Емкость канала измеряется в битах на символ (или в битах на выходе на входной бит) и для двоичных каналов должна принадлежать интервалу  . Все это очень здорово, но определенная в (8) емкость не позволяет нам эффективно сравнивать каналы, поскольку процедура максимизации по источникам не вполне тривиальна. Определение емкости канала С(р) является одной из основных проблем теории информации, но к счастью рассматриваемый случай симметричного бинарного канала достаточно прост. Из (7) и (8) можно вывести результат:
. Все это очень здорово, но определенная в (8) емкость не позволяет нам эффективно сравнивать каналы, поскольку процедура максимизации по источникам не вполне тривиальна. Определение емкости канала С(р) является одной из основных проблем теории информации, но к счастью рассматриваемый случай симметричного бинарного канала достаточно прост. Из (7) и (8) можно вывести результат:
 . (9)
. (9)
При выводе (9) мы учли, что при передаче одного бита S(X) = 1 (“0” или “1” могут появиться с равной вероятностью). Если же вероятность ошибки равна 0.5 (т.е. когда p(x = 0) = p(x = 1) = Ѕ), то H(1/2) = 1 и информацию передать невозможно - сообщение полностью зашумляется!
Теорема Шенона для зашумленного канала связи утверждает, что при наличии шумов, которые описываются слагаемым  в (7) и (8), для увеличении взаимной информации нужно увеличивать S(X), характеризующую источник информации.
в (7) и (8), для увеличении взаимной информации нужно увеличивать S(X), характеризующую источник информации.
Замечание. Из теоремы Шенона для зашумленного канала следует, что пропускная способность C(p) определяет оптимальную скорость передачи информации по каналу с шумом. Оказывается, что для сообщения, содержащего большое число букв n, вероятность ошибки приема оказывается порядка 1/n, если передача идет со скоростью С(p). Эта вероятность стремится к нулю при  .
.
Коды, исправляющие ошибки.
До сих пор мы интересовались тем как информация проходит по зашумленному каналу связи и как она теряется там. Алиса не может передать больше информации, чем С(р) на передаваемый символ. Предположим, что Боб обезвреживает мину, а Алиса, находясь на некоем расстоянии, кричит ему какой провод обрезать. Если она крикнет лишь один раз “режь синий провод”, то не будет уверена в том, что он услышит ее правильно. Она будет повторять свои сообщения много раз, а Боб будет ждать пока не будет уверен, что получил правильное сообщение. Такой способ сообщений может быть достигнут даже через зашумленный канал. В этом примере можно добиться передачи желаемого сообщения жертвуя количеством передаваемой информации - число ошибок уменьшается при увеличении количества передаваемой информации. Рассмотрим более продвинутые стратегии.
Набор {0, 1} рассматривается как группа Галуа (GF(2)), в которой операции сложения, вычитания, умножения и деления выполняются по модулю 2 (т.е. 1 + 1 = 0). n- битовое слово (двоичное слово, состоящее из n битов) есть вектор, содержащий n компонент, например, 011 это вектор (0,1,1). Набор таких векторов образует векторное пространство относительно сложения, т.к., например, 011 + 101 значит (0,1,1) + (1,0,1) = (0 + 1,1 + 0,1 + 1) = (1,1,0) = 110 по стандартным правилам сложения векторов. Это аналогично выполнению операции XOR.
Эффект шума, действующего на слово u, можно записать в виде  , где вектор ошибки показывает какой бит в слове u перевернулся под действием шума. Например, u = 1001101 ® u¢ = 1101110 можно переписать в виде u¢ = u + 0100011. Код, исправляющий ошибку, есть такой набор слов, что
, где вектор ошибки показывает какой бит в слове u перевернулся под действием шума. Например, u = 1001101 ® u¢ = 1101110 можно переписать в виде u¢ = u + 0100011. Код, исправляющий ошибку, есть такой набор слов, что
 , (10)
, (10)
где Е - набор векторов ошибок, исправляемых кодом С, включая случай отсутствие ошибки (нулевой вектор е = 0). Чтобы использовать такой код Алиса и Боб договариваются какому кодовому слову u отвечает какое сообщение. Тогда Алиса будет посылать в канал только кодовые слова. Поскольку канал зашумлен, Боб получает не u, а u + e. Однако, Боб может однозначно извлечь u из u + e используя (10), т.к. по этому условию он не может принять слово u + e , если Алиса передаст какое-нибудь другое кодовое слово v.
Пример работы кода, исправляющего ошибки, приведен в таблице. Это т.н. код Хамминга. Обозначение [n, k, d] означает, что кодовые слова имеют длину n бит, всего этих кодовых слов 2k штук и все они отличаются друг от друга по крайней мере в d позициях. В силу некоей специфики условие (10) удовлетворяется для любой ошибки, которая воздействует не более чем на один бит. Другими словами, набор Е исправляемых ошибок есть {0000000, 1000000, 0100000, 0010000, 0001000, 0000100, 0000010, 0000001}. Заметим, что Е может содержать по крайней мере 2n-k членов. Отношение k/n называется нормой кода, т.к. каждый блок из n передаваемых бит содержит k бит информации, т.е. k/n битов на бит.
| Сообщение | Хаффман | Хамминг |
| 0000 | 10 | 0000000 |
| 0001 | 000 | 1010101 |
| 0010 | 001 | 0110011 |
| 0011 | 11000 | 1100110 |
| 0100 | 010 | 0001111 |
| 0101 | 11001 | 1011010 |
| 0110 | 11010 | 0111100 |
| 0111 | 1111000 | 1101001 |
| 1000 | 011 | 1111111 |
| 1001 | 11011 | 0101010 |
| 1010 | 11100 | 1001100 |
| 1011 | 111111 | 0011001 |
| 1100 | 11101 | 1110000 |
| 1101 | 111110 | 0100101 |
| 1110 | 111101 | 1000011 |
| 1111 | 1111001 | 0010110 |
Левая колонка - 16 возможных 4-битовых сообщений. Две другие колонки- закодированные версии каждого сообщения. Код Хаффмана - сжатие данных. Наиболее часто встречающиеся сообщения имеют более короткую длину. Считается, что в каждом бите сообщения нули встречаются в три раза вероятнее, чем единице. Код Хамминга - исправляющий ошибки. Каждое кодовое слово отличается от всех других по крайней мере тремя позициями. Поэтому любая единичная ошибка может быть исправлена. Код Хамминга линеен: все слова даются линейными комбинациями 1010101, 0110011, 0001111, 1111111. Они удовлетворяют проверке четности 1010101, 0110011, 0001111.
Параметр d называется “минимальным расстоянием” кода. Он важен, когда кодируется сигнал в присутствии шума, действующего на биты независимо , как в двоичном симметричном канале. Код с минимальным расстоянием d может исправить все ошибки, действующие менее чем на d/2 бит передаваемого кодового слова и при шуме, действующем независимо на биты, это является наиболее вероятным набором ошибок. На самом деле вероятность, что n-битовое слово получит m ошибок дается биномиальным распределением, поэтому если код может исправить более чем среднее количество ошибок np, исправление будет вероятнее всего удачным.
Центральный результат классической теории информации состоит в том, что существует мощный исправляющий ошибки код:
теорема Шеннона. Если норма кода удовлетворяет условию k/n < C(p) и число битов n достаточно велико, то существует двоичный код, позволяющий осуществлять связь с произвольно малой вероятностью ошибки.
Здесь вероятность ошибки - это вероятность того, что происходит неисправленная ошибка, которая заставляет Боба неверно воспринять полученное слово. Теорема Шеннона звучит очень многообещающе, поскольку из нее следует, что не нужно разрабатывать низкошумящие каналы, что является дорогостоящей и трудновыполнимой задачей. Вместо этого мы компенсируем шум техникой коррекцией ошибок при кодировании и раскодировании, т.е. используя аппарат теории информации.
В заключение - об универсальных (классических) логических элементах.
Логический элемент осуществляет логически обратимую операцию, если сигнал на входе может быть однозначно определен по сигналу на выходе. Фредкин и Тоффоли показали, что существует два (по крайней мере) универсальных ЛЭ, с помощью которых можно организовать произвольные логические операции в компьютере. Это логически полные ЛЭ Controlled-Controlled-NOT (Тоффоли) и Сontrolled SWAP (Фредкин).
ТОФФОЛИ
| a | b | c | a | b | c |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 0 |
Операция “НЕ” по выходу “с”, когда на входах a, b - логические единицы.
ФРЕДКИН
| a | b | c | a | b | c |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | Вместе с этой лекцией читают "Пелопоннесская война (431-404 гг. до н. э.)". 0 |
входы b, c - обмениваются значениями, когда на входе а -логическая единица.
ЛИТЕРАТУРА
1. A.Steane, Quantum Computing. Quant-ph/9708022
2. А.С.Холево. Введение в квантовую теорию информации. Москва, 2002. МЦНМО, 2002. - 228 с.
3. В.Н.Горбачев, А.И.Жилиба Физические основы современных информационных процессов. Ст.-Петербург, Издательство “Петербургский институт печати”, 2004.





















