Электродинамические потенциалы гармонического поля
Раздел 5. Электродинамические потенциалы гармонического поля.
5.1.Уравнения Гельмгольца.
Практически все задачи электродинамики разделяют на 2 вида:
1. прямые задачи, в которых по заданному распределению сторонних источников необходимо определить соответствующее распределение электромагнитного поля.
2. обратные задачи, в которых по заданному распределению электромагнитного поля надо определить соответствующее распределение сторонних источников.
В этом разделе рассмотрим основные методы решения прямых задач электродинамики применительно для гармонического ЭМ поля и однородных линейных изотропных сред.
Относительно мгновенных значений векторов поля задачи решают очень редко, из-за сложности их определения. Обычно задачи решают для гармонических полей с использованием метода комплексных амплитуд. При решении любых электродинамических задач очень редко используют непосредственно уравнения Максвелла. Обычно уравнения Максвелла стараются свести к известным формам дифференциальных уравнений.
Рассмотрим гармонический электромагнитный процесс. Запишем уравнения Максвелла для комплексных амплитуд:
(1)
Рекомендуемые материалы
(2)
Возьмем ротор от правой и левой части соотношения (1). Получим:
(3)
Воспользуемся известным тождеством: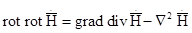 
Из 4-ого уравнения Максвелла: 
следует, что:
(4)
Подставим (4) и (2) в соотношение (3) и получим: 
или
(5)
В результате проведенных преобразований мы получили неоднородное дифференциальное уравнение, которое в математической физике называется неоднородным уравнением Гельмгольца. Это уравнение описывает волновые процессы. Векторное дифференциальное уравнение (5) можно записать в виде трех уравнений проекций:
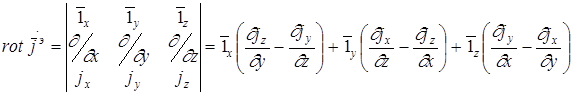
(6)
Аналогичные уравнения можно получить и для вектора напряженности поля.
(7)
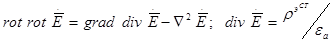
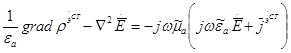
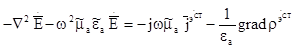
Меняя везде знаки, получим:
(8)
При анализе сред, в которых отсутствуют сторонние источники, неоднородные уравнения (5), (8) преобразуются в однородные:
(9)
Соотношения (5), (8), (9) называются уравнениями Гельмгольца относительно векторов поля.
5.2. Электродинамические потенциалы для комплексных амплитуд.
Даже уравнения Максвелла, преобразованные к уравнениям Гельмгольца в форме (5), (8), используются при решении электродинамических задач из-за сложной правой части. При решении задач для векторов поля уравнения используются только для полей без сторонних источников. Обычно, если рассматриваемые задачи со сторонними источниками, используют искусственный прием - вводят формальные поля, которые описываются некоторыми функциями, называемыми электродинамическими потенциалами. Для них решают электродинамическую задачу, а соответствующие вектора электромагнитного поля находят, используя уравнения связи между электромагнитными потенциалами и векторами поля.
Получим выражения для электродинамических потенциалов. Для этого запишем уравнения Максвелла:
(1)
(2)
(3)
(4)
Существует следующее векторное тождество:
и 
(5)
Векторную функцию 
называют векторным электрическим потенциалом. Соотношение (5) при известном однозначно определяет вектор 
. Обратное определение неоднозначно, т.е. при известном векторном поле соотношение (5) определяет неоднозначно. Известно, что 
. Поэтому, если ввести 
и 
, то соотношение (5) не изменится. Поэтому соотношение (5) определяет с точностью до градиента произвольной функции.
Подставим (5) в (2). Получим: 
или 
(6)
Воспользуемся вновь тождеством: и 
.
При этом: 
(7)
Скалярную функцию 
называют скалярным электрическим потенциалом. Знак " - " поставлен, чтобы в случае электростатических полей мы получили соотношение, связывающее напряженность электрического поля и электрический потенциал. С помощью соотношений (5) и (7) определили векторы магнитного и электрического полей через два формальных поля: поля векторного электрического потенциала и поля скалярного электрического потенциала. Получим уравнения для их определения. Подставим соотношения (5) и (7) в первое уравнение Максвелла:
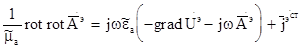
Помножим на 
, раскроем 
и раскроем скобки.
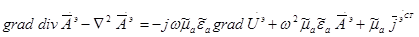
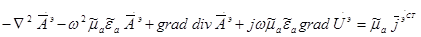
Формальные поля векторного и электрического потенциалов были введены без ограничений, т.е. это совершенно произвольные функции. Единственное ограничение — это то, что векторное поле электрического потенциала определяется точностью до градиента произвольной функции. Поэтому мы вправе ввести какие-то ограничения. Пусть таким ограничением будет:
(8)
Равенство (8) называется условием калибровки.
А теперь: 
(9)
Аналогичным образом может быть получено выражение для определения скалярного электрического потенциала. Для этого нужно воспользоваться третьим уравнением Максвелла. Вместо 
запишем соотношение (7):
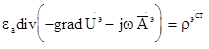
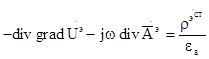
Вместо 
подставим то, чему она равна, используя условие калибровки:
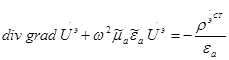
окончательно получаем: 
(10)
Таким образом, мы получили 2 уравнения: векторное дифференциальное и скалярное дифференциальное с простой правой частью. Из наших рассуждений мы можем исключить , т.е. можем свести к нахождению только . Для этого в соотношении (7) исключим , используя соотношение (8). Из соотношения (8) следует: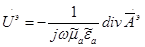
(11)
5.3. Решение неоднородных уравнений Гельмгольца.
Необходимо решить неоднородное уравнение Гельмгольца:
(1)
Если удастся решить это уравнение, то: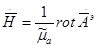 
|
|
Требуется определить поле в искомой точке Р вне объема V, причем расстояние от любой точки внутри объема до точки Р значительно больше, чем размеры объема. Выделим внутри объема V точку Q и вокруг нее построим элементарный объем DV. R — расстояние между точками Q и Р. Мы ищем интенсивность поля , возбуждаемого сторонними токами в точке Р. Эта интенсивность пропорциональна 
(2). 
— некоторое среднее значение объемной плотности тока. Размеры объема 
значительно меньше расстояния R, поэтому с протекающими в нем сторонними токами можно рассматривать как точечный источник. В силу симметрии задачи возбуждение поля в однородном изотропном пространстве точечным источником поверхность равных фаз (фазовых фронтов) будет иметь вид сферы (сферической волны расходящейся от источника на бесконечность).
Ограничимся простым случаем: когда поле гармоническое и амплитуда поля, возбуждаемого точечным источником, зависит только от r (r – расстояние от Q до P).
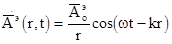
(3) – постоянная распространения, т.е. среда без потерь.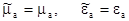 
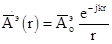
где r — радиальная координата. Последнее соотношение описывает сферическую волну. Таким образом, поле, возбуждаемое этими токами в объеме DV:
(4).
Уравнения Максвелла и вытекающие из них уравнения Гельмгольца являются линейными дифференциальными уравнениями, поэтому для них справедлив принцип суперпозиции. В данном случае принцип суперпозиции истолковывается: поле, возбуждаемое элементарными объемами, находящимися внутри объема V, можно представить как суперпозицию полей, возбуждаемых сторонними токами, протекающими внутри элементарных объемов.
(5)
Ri — расстояние от Vi до точки наблюдения.
Для того чтобы возникло равенство надо определить коэффициент пропорциональности, который может быть определен в результате предельного перехода при бесконечном увеличении числа элементарных объемов в объеме V. В математической физике, при определении общего решения уравнения Гельмгольца, этот переход осуществлен:
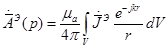
Предположим, что у нас имеются потери: 
.
(6)
Когда сторонние источники распределены по поверхности S:
(7),
r — расстояние от элемента поверхности S до точки наблюдения.
Если поверхностные токи распределены по контуру, то: 
(8).
5.4. Уравнения Максвелла с учетом магнитных токов и зарядов.
Современная физика в настоящее время исключает возможность существования магнитных зарядов и токов, тем не менее, их введение очень упрощает решение задач.
Рассмотрим пространство, в котором существуют сторонний электрический ток и заряд. В этом случае уравнения Максвелла выглядят:
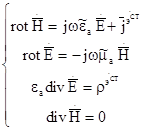
Будем предполагать, что в среде отсутствуют потери: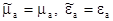 
(1)
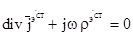
В рассматриваемой области, рассмотрим источники 
и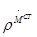 
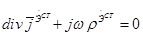
Уравнения Максвелла в этом случае будут:
(2)
Если в среде имеются и магнитные, и электрические источники, то уравнения Максвелла:
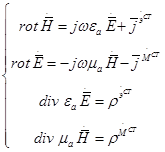
Из сопоставления систем (1) и (2) следует, что из любой из них может быть получена другая, если в исходной системе осуществить следующие перестановки:
(3)
Перестановки (3) получили название принципа перестановочной двойственности. Этот принцип позволяет в случае, если получено решение с одними сторонними источниками, получить готовое решение для других сторонних источников, не решая этой задачи, осуществив перестановки в соответствии с соотношением (3) в готовом решении задачи со сторонними источниками. В случае, когда имеются сторонние электрические источники, мы любую задачу решаем следующим образом:
Информация в лекции "Вопросы к экзамену по зарубежной литературе XX века" поможет Вам.
Воспользуемся принципом перестановочной двойственности. Получим соотношения для сторонних магнитных источников:
В том случае, если в рассматриваемой задаче имеются и те, и другие источники, получаем:
