Энергия электростатического поля

§ 2.5. Энергия электростатического поля.

         Поместим точечный источник – заряд  в поле потенциала . Так как  - это работа по перемещению положительного единичного заряда из 1 на бесконечность, то:

                         -                  (2.42)

энергия заряда  в поле .

         Для двух точечных зарядов  и  работа при перемещении их от  до бесконечности определяет потенциальную энергию:

,   (2.43)

где  и  - потенциалы, создаваемые первым! и вторым зарядом!, соответственно, в месте, где помещены  и . Для случая нескольких точечных зарядов:

.                     (2.44)

Это энергия взаимодействия системы дискретных зарядов.

Рекомендуемые материалы

         Рассмотрим теперь случай, когда заряды распределены непрерывно. Зная, что , и переходя от суммирования к интегрированию, получаем:

,                          (2.45)

где  - потенциал, создаваемый всеми зарядами системы в элементе . Это выражение кажется простым обобщением предыдущей формулы, но это не так – они различны, поскольку , входящий в формулы (2.44) и (2.45), имеет разный смысл.

         Для объяснения рассмотрим следующий пример. Пусть система состоит из двух шаров с зарядами  и . Расстояние между ними много больше их размеров, т.е.  и  - точечные заряды. Энергия системы имеет вид (2.43), где - потенциал, создаваемый  в точке, где помещен , потенциал  создан  в точке, где помещен .

         Воспользуемся теперь формулой (2.45). Интеграл должен разбиться на два по объемам  и :

.                   (2.46)

Разобъем заряд первого шара на элементарные . На этот заряд действует потенциал, создаваемый всеми зарядами второго шара и, кроме того, зарядами собственного шара:

                           (2.47).

То же самое и для элементарного заряда второго шара. Действующий на него потенциал:

.                           (2.48)

С учетом (2.47) и (2.48) можно (2.46) записать:

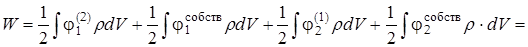
,                          (2.49)

где  - энергия взаимодействия шаров зарядами  и ;  и  - собственные энергии этих шаров.

.              (2.50)

Это формула для системы из - шаров. Она содержит энергию взаимодействия зарядов шаров и собственные энергии.

         Теперь получим формулу (2.45), но не при наличии потенциала, а в присутствии электростатического поля. Рассмотрим это на примере плоского конденсатора и его энергии. Для начала выведем выражение для энергии уединенного проводника, имеющего заряд  и потенциал . Поскольку  во всех точках проводника одинаков, вынесем его за знак интеграла в формуле (2.45). Тогда оставшийся интеграл – это заряд  на проводнике;

.

Теперь рассмотрим энергию конденсатора, где  и  - заряд и потенциал положительно заряженной обкладки,  и  - то же для отрицательно заряженной обкладки. Так как , то:

.

Учтем, что . Тогда:

.                        (2.51)

Подставив: ;    ;      , получим:

           -                 (2.52)

электрическая энергия конденсатора. Плотность энергии с учетом того, что  и - векторы:

.                                        (2.53)

Видно, что носителем энергии является поле, и энергия локализована во всем пространстве, где есть электрическое поле. Так как:

,

то  - плотность энергии положительна.

Для общего случая, когда  изменяется в пространстве:

.                             (2.54)

Сравним формулы (2.45) и (2.54). В первой носителями энергии являются заряды, и энергия локализована на зарядах. В (2.54) носителем энергии является поле, и энергия локализована во всем пространстве, где имеется поле.

         Обе формулы представляют полную энергию, включающую энергию взаимодействия и собственную энергию. Покажем это для (2.54) на примере двух заряженных тел в пустоте, создающих в пространстве поля  и , соответственно. По принципу суперпозиции:

,

.

Полная энергия системы:

,     (2.55)

где  и  - собственные энергии первого и второго тел, - энергия их взаимодействия.  и  всегда положительны,  может быть как положительной, так и отрицательной. Полная энергия  также всегда положительна. Если в формулу (2.53) подставить , тогда:

.                              (2.56)

         Первое слагаемое – это плотность энергии поля в вакууме. Второе – плотность энергии, связанная с поляризацией диэлектрика.

Пример.

1. Определить энергию  объемно заряженного шара. Даны  и .

Согласно (1.24) и (1.25) примера 3 §1.4:

для    :    ;                  для    :    ;

;          .

Найдем теперь полную энергию по формуле (2.54):

                   .

                             .

Видно, что                                      .

Полная энергия:

.                     (2.57)

2. Энергия диполя во внешнем поле.

Поле создают потенциалы  в точках, где расположены заряды  (см.рис.2.20). Тогда энергия этих зарядов по (2.42) равняется:

.

Ещё посмотрите лекцию "112 Антианемические средства, используемые при гипохромных анемиях" по этой теме.

Так как , разложим  в ряд:

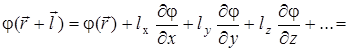
,                   (2.58)

где  - компоненты ;  - компоненты .

.               (2.59)

         Из (2.59) видно, что в поле  диполь ориентируется так, что  (минимум энергии). Рассмотрение механизма поворота вектора  связано с появлением вращающего момента, так как на заряды  со стороны поля  действуют противоположно направленные силы .