Стационарные состояния

Глава V.         Теория      атома        водорода       и        водородоподобных    атомов.

§ 5.1.  Стационарные состояния.

Стационарными называют состояния, энергия системы в которых не зависит от времени. Таким образом, чтобы найти энергии в этих состояниях, необходимо решить стационарное уравнение Шредингера. Рассмотрим потенциальную энергию частицы: . Решим уравнение Шредингера для потенциальной составляющей: . Введём следующие обозначения:; . Осуществим замену переменных: , ; . Тогда, после подстановки новых переменных наше уравнение примет вид: . Упростим данное выражение: . Произведём дифференцирование: . Раскроем скобки и запишем в виде обыкновенного дифференциального уравнения: ,       (1). Решение данного уравнения будем искать по тому же алгоритму, что и для гармонического осциллятора.

Рекомендуем посмотреть лекцию "2.3. Основное уравнение гидростатики".

1. Рассмотрим сначала асимптотическое решение при . Тогда уравнение (1) преобразуется к виду: . Решением его, очевидно, будет функция . Чтобы решение было ограничено на бесконечности, необходимо положить . Таким образом, .

2. Теперь рассмотрим ассимптотику при . Принебрегая членами со степенями , получим из уравнения Шредингера: . Решение данного уравнения будем искать в виде: . Подставляем предпологаемое решение в преобразованное уравнение Шредингера. Получим: ,  , ; . Мы получили уравнение относительно . Раскроем скобки, приведём его к стандартному виду и найдём решение. , . Решением этого алгебраического уравнения будет . Или, так как , . Если , то . При , . Поэтому данное значение  придётся отбросить. Таким образом, остаётся решение такого вида: .

Итак, у нас есть решения при асимптотическом стремлении  к нулю и к бесконечности. Тогда решение для радиальной составляющей волновой функции мы будем искать в виде произведения: . Здесь  – некоторая функция, которая определяет поведение  в промежутке от нуля до бесконечности. Подставляем данный вид решения в уравнение (1). После взятия производных и упрощения, получим:       (2). Введём ограничения на функцию : она не должна на бесконечности расти быстрее, чем , а в нуле должна либо обращаться в ноль, либо быть константой. Эти обстоятельства наводит на мысль, что функцию  следует искать в виде полинома: . Подставим этот предполагаемый вид решения в уравнение (2). Вычислим первую и вторую производные: , . Тогда:

.

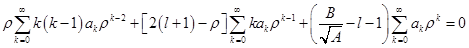
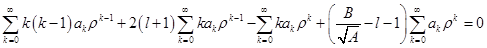
Данный многочлен будет равен нулю только в том случае, когда коэффициенты при каждой степени  будут равны нулю. Запишем это условие: . Данное соотношение даёт рекуррентную формулу для коэффициентов : . Оценим коэффициенты  при : , ; . Таким образом,  и . Тогда при каком-нибудь малом значении  многочлен можно оборвать: , а . Данное условие будет выполнено, если коэффициент при  будет равен нулю: , ; . Вернёмся к обозначениям  и : , . . Сократим: , . Из этой формулы следует, что энергия зависит от и . Введём следующее обозначение: . Тогда , где . Таким образом, решая уравнение Шредингера, мы нашли энергии водородоподобного атома, то есть нашли собственные значения оператора Гамильтона. То же самое значение для энергий мы получили, исходя только из постулатов Бора и правила квантования. Схема энергетических уровней будет совпадать со схемой энергетических уровней по Бору. Теория Бора не объясняет, почему главное квантовое число имеет своим первым значением 1. Квантовая же теория показывает, что при  и  минимально возможное значение главного квантового числа будет 1. Напомним, как называются числа ,  и .  – орбитальное квантовое число,  – радиальное квантовое число и  – главное квантовое число.

Теория Бора исходила из тех принципов, что электроны движутся в атоме по круговым орбитам по законам классической механики, но в противоречие классической электродинамике ускоренно движущиеся электроны не излучают. В квантовой теории интерпретация движения электронов иная. Вообще нельзя говорить о движении электронов по какой-либо траектории, то есть нельзя представить координаты электрона как функцию времени. Поэтому используется представление о состоянии движения электрона, описываемом той или иной волновой функцией. Причём состояние движения электрона не всегда имеет классический аналог. Например, рассмотрим состояние электрона, при котором . Это значит, в силу правила квантования: , что так как скорость движения электрона отлична от нуля, , то есть плечо не имеет длины. Это возможно в том случае, если электрон движется вдоль радиуса, то есть проходит на пути своего движения сквозь ядро.