Частица в одномерной потенциальной яме

§ 4.2. Частица в одномерной потенциальной яме.

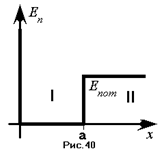
Мы будем рассматривать связанное движение частиц. Движение частицы в потенциальной яме является примером такого движения. Потенциальной ямой называется область пространства, в которой потенциальная энергия меньше, чем в окружающем пространстве. В частности движение электрона в кулоновском потенциале ядра есть движение в потенциальной яме. Рассмотрим простейший случай одномерной потенциальной ямы с бесконечно высокими стенками.

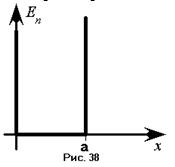
Её можно описать следующими уравнениями: . Так как энергия частицы внутри ямы нулевая, то существует только вероятность нахождения частицы внутри ямы, так как она не может преодолеть стенки ямы: . Так как волновая функция имеет смысл плотности вероятности нахождения частицы в той или иной точке пространства, то и . Таким образом имеет смысл искать волновую функцию только внутри ямы. Стационарное уравнение Шредингера внутри ямы имеет вид: . Здесь  – энергия частицы. Запишем граничные условия:      (1). Введём следующее обозначение: . Тогда уравнение Шредингера примет вид: . Решением данного уравнения является функция . Используем первое граничное условие: , следовательно, . Но , поэтому . Применим теперь второе граничное условие: . То есть . Получается, что  зависит от . Тогда . Очевидно, что  принимает дискретные значения. Вспоминая, что , получим с учётом последнего выражения: . Отсюда , причём минимальная энергия равна: . Таким образом, энергию движущейся частицы внутри потенциальной ямы мы можем представить в виде энергетических уровней. Волновая функция такой частицы имеет вид: .

Волновая функция основного состояния . Эта функция внутри ямы изменяется и с уменьшением размера ямы энергия возрастает. Найдём константу  из условия нормировки: вероятность нахождения частицы внутри ямы равна 1: . . Отсюда  и для волновой функции имеем: . В случае конечных значений потенциальной энергии существует ненулевая вероятность прохождения частицы за пределы ямы. Мы докажем этот факт чуть позже.

Рассмотрим случай несимметричной ямы: один барьер бесконечный, а другой имеет конечные размеры. Рассмотрим движение в двух областях:  и .

1. В первой области уравнение Шредингера имеет вид . Вводя обозначение , получим: . Решение этого уравнения аналогично предыдущему пункту: . Из граничных условий, которые соответствуют (1), получаем, что  и .

Рекомендация для Вас - Лекция 10 - Алгебраические критерии устойчивости.

2. Во второй области уравнение Шредингера имеет вид:  или . Введём здесь обозначение: . С учётом обозначения можно записать: . Решение данного уравнения зависит от . Имеют место два случая:  и   в зависимости от знака . Разберём каждый случай.

1. Случай . Общий вид решения исходного уравнения задаётся формулой: . Волновая функция частоты должна быть непрерывна. Этот факт математически выражается так:  и    (2). Подставляя значения функций, получим:  или  . Считая производные и удовлетворяя равенству (2), получим:  или . Мы получили систему уравнений: . Эти условия всегда могут быть удовлетворены. Поэтому в случае  спектр энергии непрерывен, частица при своём движении не локализована в конечной области пространства, её движение инфинитно.

2. Случай . В этом случае . Решением этого уравнения будет функция следующего вида: . Первое слагаемое в данном уравнении не имеет физического смысла, иначе волновая функция неограниченно возрастать с увеличением . Поэтому мы обязаны положить . Получится уравнение: . Эта функция ограничена для любого значения энергии. Однако даже если энергия частицы меньше энергии потенциального барьера, то всё равно существует вероятность обнаружить частицу за барьером. С ростом  волновая функция убывает.

Попробуем теперь найти возможные значения энергии, которые будут принимать частица в том случае, если её энергия будет меньше энергии потенциального барьера: . Рассмотрим уравнения волновых функций в двух различных областях: , . Из соображений конечности волновой функции и её непрерывности мы можем записать:  и . Подставляя конкретный вид соответствующей функции, получим:  и . Разделим второе уравнение на первое. В результате получим: ,    (3). Найдём возможные значения  и , чтобы найти возможные значения энергии. Известно, что , а . Возвращаясь к выражениям (3) и используя только что приведённые, получим: . Подставляя выражение для  в предыдущую формулу, получим ,  , так как . Тогда , где . Решаем последнее уравнение графически. Точки пересечения дают значения энергии.

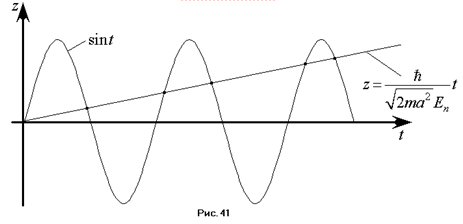
Так как прямая неограничено возрастает, а синус – функция ограниченная, то число точек пересечения будет конечно. Таким образом, и спектр энергии будет дискретным. Итак, мы получили различные выражения для различных видов ям и энергий частицы. Если яма имеет бесконечную глубину, то энергия будет принимать дискретные значения, причём набор этих значений будет бесконечен. Если яма имеет конечную глубину, то в зависимости от энергии частицы будет образовывать либо непрерывный спектр в случае , либо дискретный в случае .