Совместная работа газопровода и компрессорных станций
VIII Совместная работа газопровода и компрессорных станций
Режимы работы трубопровода и компрессорных станций (КС) связаны между собой: расход в трубопроводе равен подаче КС, давление нагнетания соответствует давлению в начале перегона между станциями, а давление всасывания следующей КС равно давлению в конце перегона.
Любые изменения режима работы КС приводят к изменениям режима работы трубопровода, и наоборот. Поэтому нельзя определить пропускную способность газопровода при помощи одной только формулы расхода. Пропускную способность газопровода также нельзя найти, пользуясь только характеристиками нагнетателей или только аналитическими выражениями этих характеристик.
Трубопровод и КС следует рассматривать как единое целое, и в технологическом расчете газопровода режимы работы трубопровода и КС должны быть согласованы. Это согласование может быть осуществлено совместным решением уравнений характеристик КС и характеристики перегонов между станциями.
Уравнение характеристики КС возьмем в виде  , а уравнение характеристики трубопровода (перегона между КС) удобно выразить так:
, а уравнение характеристики трубопровода (перегона между КС) удобно выразить так:  ,
,
 ;
;  ;
; 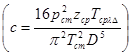
где  – постоянный коэффициент;
– постоянный коэффициент;  – длина перегона.
– длина перегона.
Рассмотрим простейший магистральный газопровод с одной промежуточной КС (рис. 5.12).
Рекомендуемые материалы
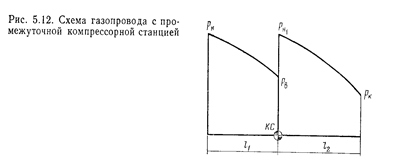
Требуется рассчитать режим работы газопровода как единой газодинамической системы, а именно определить пропускную способность газопровода Q и давления всасывания  и нагнетания
и нагнетания  КС при известных (и постоянных) значениях давления в начале
КС при известных (и постоянных) значениях давления в начале  и в конце
и в конце  газопровода. Это можно сделать, решив совместно уравнения характеристик двух перегонов и КС газопровода
газопровода. Это можно сделать, решив совместно уравнения характеристик двух перегонов и КС газопровода
 ;
;  ;
;  . (8.1)
. (8.1)
При этом предполагается, что коэффициент  , равный
, равный
 , (8.2)
, (8.2)
практически одинаков для первого и второго перегонов. Для его определения необходимо задаться в первом приближении значениями  ,
,  и
и  . После определения
. После определения  ,
,  и
и  , а также в процессе теплового расчета перегонов их значения могут быть уточнены. Отметим, что принятие различных значений коэффициента
, а также в процессе теплового расчета перегонов их значения могут быть уточнены. Отметим, что принятие различных значений коэффициента  для каждого из перегонов газопровода не осложнило бы решение задачи. Решая систему уравнений (8.1), находим
для каждого из перегонов газопровода не осложнило бы решение задачи. Решая систему уравнений (8.1), находим
 . (8.3)
. (8.3)
При неработающей КС уравнение (8.3) превращается в известное уравнение расхода участка газопровода
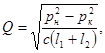
поскольку в этом случае  , а
, а  . Из уравнения (8.3) следует очень важный практический вывод: при прочих равных условиях (неизменных значениях давлений в начале и конце газопровода и заданной характеристике КС) пропускная способность газопровода как системы тем больше, чем ближе КС будет размещена к началу газопровода.
. Из уравнения (8.3) следует очень важный практический вывод: при прочих равных условиях (неизменных значениях давлений в начале и конце газопровода и заданной характеристике КС) пропускная способность газопровода как системы тем больше, чем ближе КС будет размещена к началу газопровода.
Очевидно, что при этом одновременно будут возрастать давления на входе и выходе КС. Увеличение пропускной способности газопровода при смещении КС к его началу объясняется повышением степени сжатия КС вследствие уменьшения объемной производительности на ее всасывании (растет давление  ), а также некоторым повышением среднего давления для обоих перегонов, что вызывает расход энергии на преодоление сил трения при движении газа по трубопроводу (снижается средняя скорость движения газа на перегоне).
), а также некоторым повышением среднего давления для обоих перегонов, что вызывает расход энергии на преодоление сил трения при движении газа по трубопроводу (снижается средняя скорость движения газа на перегоне).
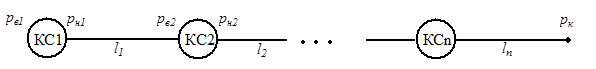
Для газопровода с  компрессорными станциями имеем
компрессорными станциями имеем
 ;
;  ;
;
 ;
;  ;
;
…………………………………………….……
 ;
;  (8.4)
(8.4)
Обозначив  , и найдя из первой пары уравнений
, и найдя из первой пары уравнений  , из второй
, из второй  и т.д., получим, что для КС, номер которой равен
и т.д., получим, что для КС, номер которой равен  ,
,
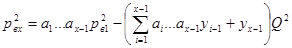
 (8.5)
(8.5)
Для конечной точки газопровода
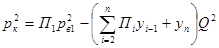
где  .
.
Отсюда расход в системе КС – трубопровод
 . (8.6)
. (8.6)
Если станции однотипные и перегоны между ними одинаковые (за исключением последнего, длина которого зависит от давления рк), т. е. если
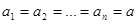
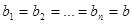
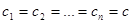
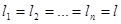
то
 ,
, 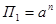
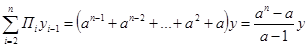
и формула (8.6) станет проще
 (8.7)
(8.7)
Если начальной точкой газопровода считать не всасывающий, а нагнетательный коллектор головной компрессорной станции, где давление равно рН1, то из системы (8.4) надо будет исключить первое уравнение. Тогда
 (8.8)
(8.8)
Из (8.6), (8.7) и (8.8) видно, что пропускная способность газопровода в первую очередь зависит от давления в начальной точке газопровода ( или
или  ), даже незначительное снижение этого давления приводит к ощутимому уменьшению пропускной способности газопровода (
), даже незначительное снижение этого давления приводит к ощутимому уменьшению пропускной способности газопровода ( ).
).
Давление в конечной точке газопровода, напротив, оказывает незначительное влияние на его пропускную способность; оно может изменяться в довольно большом диапазоне, и на пропускной способности газопровода это существенно не отразится. Влияние  на
на  тем меньше, чем больше число станций
тем меньше, чем больше число станций  , влияние начального давления на пропускную способность газопровода с увеличением
, влияние начального давления на пропускную способность газопровода с увеличением  , наоборот, возрастает.
, наоборот, возрастает.
Из (8.6), (8.7) и (8.8) также следует, что на пропускную способность газопровода влияет расположение компрессорных станций: чем меньше расстояния между ними, тем меньше  и, следовательно, тем больше
и, следовательно, тем больше  . Но при сближении станций возрастут давления
. Но при сближении станций возрастут давления  и
и  . Это – ограничение: давление в любой точке газопровода не должно превышать допустимого из условия прочности.
. Это – ограничение: давление в любой точке газопровода не должно превышать допустимого из условия прочности.
При однотипных станциях и одинаковых перегонах между ними упрощаются также выражения, определяющие давления всасывания и нагнетания: для произвольно взятой компрессорной станции  вместо (8.5) получаем
вместо (8.5) получаем
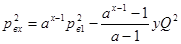
 (8.9)
(8.9)
Отсюда следует, что давления всасывания и нагнетания даже при однотипных КС и при перегонах одной и той же протяженности практически не бывают одинаковыми на всех станциях. Одинаковыми эти давления будут при расходе, который получается из первой пары уравнений (8.4):
 (8.10)
(8.10)
Если это подставить в (8.9), то на любой станции  окажется, что
окажется, что  и
и  .
.
Давление  , при котором все это может быть обеспечено, выразится
, при котором все это может быть обеспечено, выразится
 .
.
1. Изменения давления  вызывают изменения давлений всасывания и нагнетания (
вызывают изменения давлений всасывания и нагнетания ( и
и  ) на КС. Рассмотрим, как это происходит. Пусть давление
) на КС. Рассмотрим, как это происходит. Пусть давление  повысилось на
повысилось на  . Если бы расход оставался неизменным, то для перегона между последней КС и конечным пунктом газопровода
. Если бы расход оставался неизменным, то для перегона между последней КС и конечным пунктом газопровода
 .
.
Отсюда следует, что
 (8.11)
(8.11)
т. е. прирост давления в начале перегона меньше величины, на которую повысилось давление в конце перегона.
На компрессорной станции повышение давления всасывания ( ) по сравнению с повышением давления нагнетания (
) по сравнению с повышением давления нагнетания ( ) определяется из сопоставления отношений давления (степеней сжатия). При неизменном расходе
) определяется из сопоставления отношений давления (степеней сжатия). При неизменном расходе  . Отсюда следует, что
. Отсюда следует, что
 (8.12)
(8.12)
Однако в действующем газопроводе изменения давления  связаны с изменением отбора газа в конечном пункте газопровода; увеличение
связаны с изменением отбора газа в конечном пункте газопровода; увеличение  происходит при уменьшении отбора. Если это учесть, то неравенства (8.11) и (8.12) усилятся.
происходит при уменьшении отбора. Если это учесть, то неравенства (8.11) и (8.12) усилятся.
Таким образом, на участке последняя КС – конечный пункт газопровода  .
.
Рекомендуем посмотреть лекцию "6 Проверка контекстных условий".
Такой же вывод следует и для остальных станций и перегонов между ними. Но заметными изменения  и
и  при изменении
при изменении  бывают лишь на последних двух – трех станциях. На последней КС
бывают лишь на последних двух – трех станциях. На последней КС  и
и  – самые большие, на предпоследней они значительно меньше, а на остальных КС давления
– самые большие, на предпоследней они значительно меньше, а на остальных КС давления  и
и  практически не изменяются.
практически не изменяются.
2. Теперь рассмотрим, как будут изменяться давления  и
и  на КС при изменении давления в начальной точке газопровода. Пусть давление
на КС при изменении давления в начальной точке газопровода. Пусть давление  возросло на
возросло на  . Считая сначала, что расход не изменился, получим, как и прежде из сравнения степеней сжатия, что
. Считая сначала, что расход не изменился, получим, как и прежде из сравнения степеней сжатия, что  , а из равенства разностей квадратов давлений для перегона между первой и второй станциями
, а из равенства разностей квадратов давлений для перегона между первой и второй станциями  .
.
Для второй станции окажется, что  , для перегона между второй и третьей станциями
, для перегона между второй и третьей станциями  и т. Д. Но, как уже было сказано, изменение давления
и т. Д. Но, как уже было сказано, изменение давления  сопряжено с изменением подачи газа в газопровод, при этом чем больше число КС, тем больше увеличивается расход при повышении давления
сопряжено с изменением подачи газа в газопровод, при этом чем больше число КС, тем больше увеличивается расход при повышении давления  . Увеличение расхода приведет к уменьшению степени сжатия, а это, как нетрудно понять,– к уменьшению
. Увеличение расхода приведет к уменьшению степени сжатия, а это, как нетрудно понять,– к уменьшению  . В результате неравенства
. В результате неравенства  окажутся либо ослабленными, либо знак у них переменится на обратный. То же получается и с неравенствами для перегонов между станциями. Таким образом, в общем случае нельзя сделать вывод о том, что больше –
окажутся либо ослабленными, либо знак у них переменится на обратный. То же получается и с неравенствами для перегонов между станциями. Таким образом, в общем случае нельзя сделать вывод о том, что больше –  или
или  и как эти величины будут изменяться от станции к станции – увеличиваться или уменьшаться. Можно лишь сказать, что при увеличении подачи газа в газопровод давления
и как эти величины будут изменяться от станции к станции – увеличиваться или уменьшаться. Можно лишь сказать, что при увеличении подачи газа в газопровод давления  и
и  повысятся, линии падения давлений поднимутся, а при уменьшении подачи газа – наоборот.
повысятся, линии падения давлений поднимутся, а при уменьшении подачи газа – наоборот.
Для сравнения заметим, что при увеличении отбора газа давления  и
и  уменьшатся и линии падения давлений на перегонах между станциями снизятся.
уменьшатся и линии падения давлений на перегонах между станциями снизятся.






















