Методы распознавания образов
Лекция № 17. МЕТОДЫ РАСПОЗНАВАНИЯ ОБРАЗОВ
Различают следующие группы методов распознавания:
- Методы функций близости
- Методы дискриминантных функций
- Статистические методы распознавания.
- Лингвистические методы
- Эвристические методы.
Первые три группы методов ориентированы на анализ признаков, выражаемых числами либо векторами с числовыми компонентами.
Группа лингвистических методов обеспечивает распознавание образов на основе анализа их структуры, описываемой соответствующими структурными признаками и отношениями между ними.
Рекомендуемые материалы
Группа эвристических методов объединяет характерные приемы и логические процедуры, используемые человеком при распознавании образов.
Методы функций близости
Методы данной группы основаны на использовании функций, оценивающих меру близости между распознаваемым образом с вектором x* = (x*1,….,x*n), и эталонными образами различных классов, представленными векторами xi = (xi1,…, xin), i=1,…,N, где i – номер класса образов.
Процедура распознавания согласно данному методу состоит в вычислении расстояния между точкой распознаваемого образа и каждой из точек, представляющих эталонный образ, т.е. в вычислении всех значений di , i=1,…,N . Образ относится к классу, для которого значение di имеет наименьшее значение среди всех i=1,…,N .
Функция, ставящая в соответствие каждой паре векторов xi, x* вещественное число как меру их близости, т.е. определяющая расстояние между ними может быть достаточно произвольной. В математике такую функцию называют метрикой пространства. Она должна удовлетворять следующим аксиомам:
r(x,y)= r(y,x);
r(x,y) > 0, если x не равен y и r(x,y)=0 если x=y;
r(x,y) <= r(x,z)+ r(z,y)
Перечисленным аксиомам удовлетворяют, в частности, следующие функции
ai=[sum(xij ‑ xj*)2]1/2, j=1,2,…n.
bi=sum[abs (xi ‑ xj*)], j=1,2,…n.
ci=max abs (xi ‑ xj*), j=1,2,…n.
Первая из них называется евклидовой нормой векторного пространства. Соответственно пространства, в которых в качестве метрики используется указанная функция называется Евклидовым пространством.
Часто в качестве функции близости выбирают среднеквадратическую разность координат распознаваемого образа x* и эталона xi, т.е. функцию
di = (1/n) sum(xij ‑ xj*)2, j=1,2,…n.
Величина di геометрически интерпретируется как квадрат расстояния между точками в пространстве признаков, отнесенный к размерности пространства.
Часто оказывается, что разные признаки неодинаково важны при распознавании. С целью учета данного обстоятельства при вычислении функций близости разности координат, соответствующие более важным признакам умножают на большие коэффициенты, а менее важным – на меньшие.
В таком случае di = (1/n) sum wj (xij ‑ xj*)2, j=1,2,…n,
где wj – весовые коэффициенты.
Введение весовых коэффициентов эквивалентно масштабированию осей пространства признаков и, соответственно растяжению либо сжатию пространства в отдельных направлениях.
Указанные деформации пространства признаков преследуют цель такого размещения точек эталонных образов, которое соответствует наиболее надежному распознаванию в условиях значительного разброса образов каждого класса в окрестности точки эталонного образа.
Группы близких друг другу точек образов (скопления образов) в пространстве признаков называют кластерами, а задачу выделения таких групп – задачей кластеризации.
Задачу выявления кластеров относят к задачам распознавания образов без учителя, т.е. к задачам распознавания в условиях отсутствия примера правильного распознавания.
Методы дискриминантных функций
Идея методов данной группы состоит в построении функций, определяющих в пространстве образов границы, разделяющие пространство на области, соответствующие классам образов. Простейшими и наиболее часто используемыми функциями такого рода являются функции, линейно зависящие от значений признаков. Им в пространстве признаков соответствуют разделяющие поверхности в виде гиперплоскостей. В случае двумерного пространства признаков в качестве разделяющей функции выступает прямая линия.
Общий вид линейной решающей функции задается формулой
d(x)=w1 x1 + w2 x2 +…+ wn xn + wn+1 = Wx+wn
где x - вектор образа, w=( w1, w2,…wn) – вектор весовых коэффициентов.
В случае разбиения на два класса X1 и X2 дискриминантная функция d(x) позволяет осуществить распознавание в соответствии с правилом:
x принадлежит X1, если d(x)>0;
x принадлежит X2, если d(x)<0.
Если d(x)=0, то имеет место случай неопределенности.
В случае разбиения на несколько классов вводится несколько функций. При этом каждому классу образов ставится в соответствие определенная комбинация знаков дискриминационных функций.
Например, если введены три дискриминантные функции, то возможен следующий вариант выделения классов образов:
x принадлежит X1, если d1(x)>0, d2(x)<0, d3(x)<0;
x принадлежит X2, если d(x)<0, d2(x)>0, d3(x)<0;
x принадлежит X3, если d(x)<0, d2(x)<0, d3(x)>0.
При этом считается, что для других комбинаций значений d1(x), d2(x), d3(x) имеет место случай неопределенности.
Разновидностью метода дискриминантных функций является метод решающих функций. В нем при наличии m классов предполагается существование m функций di(x), называемых решающими, таких, что если x принадлежит Xi, то di(x) > dj(x) для всех j не равных i,т.е. решающая функция di(x) имеет максимальное значение среди всех функций dj(x), j=1,...,n..
Иллюстрацией такого метода может служить классификатор, основанный на оценке минимума евклидова расстояния в пространстве признаков между точкой образа и эталоном. Покажем это.
Будем считать, что задано m классов с эталонами xi = (xi1,…, xin), i=1,…,m.
Евклидово расстояние между вектором признаков распознаваемого образа x и вектором эталонного образа определяется формулой ||xi ‑ x|| = [sum(xij ‑ xj)2]1/2, j=1,2,…n.
Вектор x будет отнесен к классу i, для которого значение ||xi ‑ x*|| минимально.
Вместо расстояния можно сравнивать квадрат расстояния, т.е.
||xi ‑ x||2 = (xi ‑ x)( xi ‑ x)т = x x - 2x xi + xi xi
Поскольку величина x x одинакова для всех i, минимум функции ||xi ‑ x||2 будет совпадать с максимумом решающей функции
di(x) = 2x xi - xi xi.
то есть x принадлежит Xi, если di(x) > dj(x) для всех j не равных i.
Т.о. машина, классифицирующая по минимуму расстояния, основывается на линейных решающих функциях. Общая структура такой машины, использует решающие функции вида
di (x)=wi1 x1 + wi2 x2 +…+ win xn + wi n+1
Она может быть наглядно представлена соответствующей структурной схемой.
Для машины, осуществляющей классификацию по минимуму расстояния имеют место равенства: wij = -2xij , wi n+1 = xi xi.
Эквивалентное распознавание методом дискриминантных функций может быть осуществлено, если определить дискриминантные функции как разности dij (x)= di (x)‑ dj (x).
Достоинством метода дискриминантных функций является простая структура распознающей машины, а также возможность ее реализации преимущественно посредством преимущественно линейных решающих блоков.
Еще одним важным достоинством метода дискриминаннтных функций является возможность автоматического обучения машины правильному распознаванию по заданной (обучающей) выборке образов.
При этом алгоритм автоматического обучения оказывается весьма простым в сравнении с другими методами распознавания.
В силу указанных причин метод дискриминантных функций завоевал широкую популярность весьма часто используется на практике.
Процедуры самообученя распознаванию образов
Рассмотрим методы построения дискриминантной функции по заданной (обучающей) выборке применительно к задаче о разделении образов на два класса. Если заданы два множества образов, принадлежащих соответственно классам А и В, то решение задачи построения линейной дискриминантной функции ищется в виде вектора весовых коэффициентов W=(w1,w2,...,wn,wn+1), обладающего тем свойством, что для любого образа выполняются условия
x принадлежит классу A, если [sum(wjxj ‑ xj)+ wn+1]>0, j=1,2,…n.
x принадлежит классу B, если [sum(wjxj ‑ xj)+ wn+1]<0, j=1,2,…n.
Если обучающую выборку составляют N образов обоих классов, задача сводится к отысканию вектора w, обеспечивающего справедливость системы неравенств Если обучающую выборку составляют N образов обоих классов, задача сводится к отысканию вектора w, обеспечивающего справедливость системы неравенств
x11wi+x21w2+...+xn1wn+wn+1>0;
x12wi+x22w2+...+xn2wn+wn+1<0;
................................................
x1iwi+x2iw2+...+xniwn+wn+1>0;
................................................
x1Nwi+x2Nw2+...+xnNwn+wn+1>0;
здесь xi=(xi1,xi2,...,xin,xin+1) - вектор значений признаков образа из обучающей выборки, знак > соответствует векторам образов x, принадлежащих классу A, а знак < - векторам x, принадлежащих классу B.
Искомый вектор w существует, если классы A и B разделимы и не существует в противном случае. Значения компонент вектора w могут быть найдены либо предварительно, на этапе, предшествующем аппаратной реализации СРО, либо непосредственно самой СРО в процессе ее функционирования. Последний из указанных подходов обеспечивает большую гибкость и автономность СРО. Рассмотрим его на примере устройства, называемого перцентроном. изобретенного в 1957 году американским ученым Розенблатом. Схематичное представление перцентрона, обеспечивающего отнесение образа к одному из двух классов, представлено на следующем рисунке.
Сетчатка S Сетчатка A Сетчатка R
о о x1
о
о о x2
о
о о x3
о (sum)-------> R (реакция)
о о xi
о
о о xn
о
о о x n+1
Устройство состоит из сетчатки сенсорных элементов S, которые случайным образом соединены с ассоциативными элементами сетчатки A. Каждый элемент второй сетчатки воспроизводит выходной сигнал только в том случае, если достаточное число сенсорных элементов, соединенных с его входом, находятся в возбужденном состоянии. Реакция всей системы R пропорциональна сумме взятых с определенными весами реакций элементов ассоциативной сетчатки.
Обозначив через xi реакцию i-го ассоциативного элемента и через wi - весовой коэффициент реакции i-го ассоциативного элемента, реакцию системы можно записать как R=sum(wjxj), j=1,..,n . Если R>0, то предъявленный системе образ принадлежит классу A, а если R<0, то образ относится к классу B. Описание этой процедуры классификации соответствует рассмотренным нами раньше принципам классификации, и, очевидно, перцентронная модель распознавания образов представляет собой, за исключением сенсорной сетчатки, реализацию линейной дискриминантной функции. Принятый в перцентроне принцип формирования значений x1, x2,...,xn соответствует некоторому алгоритму формирования признаков на основе сигналов первичных датчиков.
В общем случае может быть несколько элементов R, формирующих реакцию перцептрона. В таком случае говорят о присутствии в перцептроне сетчатки R реагирующих элементов.
Схему перцентрона можно распространить на случай, когда число классов более двух, путем увеличения числа элементов сетчатки R до числа различаемых классов и введение блока определения максимальной реакции в соответствии со схемой, представленной на выше приведенном рисунке. При этом образ причисляется к классу с номером i, если Ri>Rj, для всех j.
Процесс обучения перцентрона состоит в подборе значений весовых коэффициентов wj так, чтобы выходной сигнал соответствовал тому классу, которому принадлежит распознаваемый образ.
Рассмотрим алгоритм действия перцентрона на примере распознавания объектов двух классов: A и B. Объектам класса A должно соответствовать значение R = +1, а классу B - значение R = -1.
Алгоритм обучения состоит в следующем.
Если очередной образ x принадлежит классу A, но R<0 (имеет место ошибка распознавания), тогда коэффициенты wj c индексами, которым соответствуют значения xj>0, увеличивают на некоторую величину dw, а остальные коэффициенты wj уменьшают на dw. При этом значение реакции R получает приращение в сторону ее положительных значений, соответствующих правильной классификации.
Если x принадлежит классу B, но R>0 (имеет место ошибка распознавания), то коэффициенты wj с индексами, которым соответствуют xj<0, увеличивают на dw, а остальные коэффициенты wj уменьшают на ту же величину. При этом значение реакции R получает приращение в сторону отрицательных значений, соответствующих правильной классификации.
Алгоритм таким образом вносит изменение в вектор весов w в том и только в том случае, если образ, предъявляемый на k-ом шаге обучения, был при выполнении этого шага неправильно классифицирован, и оставляет вектор весов w без изменений в случае правильной классификации. Доказательство сходимости данного алгоритма представлено в работе [Ту, Гонсалес]. Такое обучение в конечном итоге (при надлежащем выборе dw и линейной разделимости классов образов) приводит к получению вектора w, обеспечивающего правильную классификацию.
Статистические методы распознавания.
Статистические методы основываются на минимизации вероятности ошибки классификации. Вероятность P неправильной классификации поступившего на распознавание образа, описываемого вектором признаков x, определяется формулой
P = sum[p(i)·prob(D(x)+i | x классу i)]
где m- число классов,
p(i) = prob (x принадлежит классу i) - априорная вероятность принадлежности произвольного образа x к i-му классу (частота появления образов i-го класса),
D(x) - функция, принимающая классификационное решение (вектору признаков x ставит в соответствие номер класса i из множества {1,2,...,m}),
prob(D(x) не равно i | x принадлежит классу i) - вероятность события "D(x) не равно i" при выполнении условия принадлежности x классу i, т.е. вероятность вынесения ошибочного решения функцией D(x) для данного значения x, принадлежащего i-му классу.
Можно показать, что вероятность неправильной классификации достигает минимума, если D(x)=i в том и только в том случае, если p(x|i)·p(i)>p(x|j)·p(j), для всех i+j, где p(x|i) - плотность распределения образов i-го класса в пространстве признаков.
Согласно приведенному правилу точка x относится к тому классу, которому соответствует максимальное значение p(i) p(x|i), т.е. произведение априорной вероятности (частоты) появления образов i-го класса и плотности распределения образов i-го класса в пространстве признаков. Представленное правило классификации называется байесовским, т.к. оно следует из известной в теории вероятности формулы Байеса.
Пример. Пусть необходимо осуществить распознавание дискретных сигналов на выходе информационного канала, подверженного воздействию шума.
Каждый входной сигнал представляет собой 0 или 1. В результате передачи сигнала на выходе канала появляется величина x, на которую налагается Гауссовский шум с нулевым средним значением и дисперсией б.
Воспользуемся для синтеза классификатора, осуществляющего распознавание сигналов, байесовским правилом классификации.
В класс №1 объединим сигналы, представляющие единицы, в класс №2 - сигналы, представляющие нули. Пусть заранее известно, что в среднем из каждой 1000 сигналов a сигналов представляют собой единицы и b сигналов - нули. Тогда значения априорных вероятностей появления сигналов 1-го и 2-го классов (единиц и нулей), соответственно можно принять равными
p(1)=a/1000, p(2)=b/1000.
Т.к. шум является гауссовским, т.е. подчиняется нормальному (гауссовскому) закону распределения, то плотность распределения образов первого класса в зависимости от значения x, или, что тоже самое, вероятность получения на выходе величины x при подаче на входе сигнала 1 определяется выражением
p(x¦1) =(2piб)-1/2exp(-(x-1)2/(2б2)),
а плотность распределения в зависимости от значения x образов второго класса, т.е. вероятность получения на выходе величины x при подаче на входе сигнала 0 определяется выражением
p(x¦2)= (2piб)-1/2exp(-x2/(2б2)),
Применение байесовского решающего правила приводит к выводу, что передан сигнал класса 2, т.е. передан ноль, если
p(2) p(x¦2) > p(1) p(x¦1)
или, более конкретно, если
b exp(-x2/(2б2)) > a exp(-(x-1) 2/(2б2)),
Поделив левую часть неравенства на правую, получим
(b/a) exp((1-2 x)/(2б2)) >1,
откуда после логарифмирования находим
1-2x > 2б2 ln(a/b)
или
x < 0.5 - б2 ln(a/b)
Из полученного неравенства следует, что при a=b, т.е. при одинаковых априорных вероятностях появления сигналов 0 и 1, образу присваивается значение 0 когда x<0.5, а значение 1, когда x>0.5.
Если заранее известно, что один из сигналов появляется чаще, а другой реже, т.е. в случае неодинаковых значений a и b, порог срабатывания классификатора смещается в ту или другую сторону.
Так при a/b=2.71 (что соответствует в 2.71 раза более частой передаче единиц) и б2=0.1, образу присваивается значение 0, если x<0.4, и значение 1, если x>0.4. Если информация об априорных вероятностях распределения отсутствует, то могут быть использованы статистические методы распознавания, в основу которых положены иные, отличные от байесовского, правила классификации.
Однако, на практике наиболее распространены методы, основанные на правилах Байеса в силу их большей эффективности, а также в связи с тем обстоятельством, что в большинстве задач распознавания образов оказывается возможным задать априорные вероятности появления образов каждого класса.
Лингвистические методы распознавания образов.
Лингвистические методы распознавания образов основываются на анализе описания идеализированного изображения, представленного в виде графа или цепочки символов, являющейся фразой или предложением некоторого языка.
Рассмотрим идеализированные изображения букв, полученные в результате первого этапа лингвистического распознавания, описанного выше. Эти идеализированные изображения можно задать описаниями графов, представленных, например, в виде матриц связей, как это было сделано в рассмотренном выше примере. Это же описание можно представить фразой формального языка (выражением).
Пример. Пусть заданы три изображения буквы А, полученные в результате предварительной обработки изображений. Обозначим эти изображения идентификаторами А1, А2 и А3.
Для лингвистического описания представленных образов воспользуемся языком PDL (Picture Description Language). Словарь языка PDL включает следующие символы:
1. Имена простейших изображений (примитивов). Применительно к рассматриваемому случаю примитивы и соответствующие им имена следующие.
Изображения в виде линии, направленной:
вверх и влево (leFt), на север(north)), вверх и вправо (right), на восток(east)).
Имена: L, N, R, E .
2. Символы бинарных операций. {+,*,-} Их смысл соответствует последовательному соединению примитивов (+), соединению начал и окончаний примитивов (*), соединению только окончаний примитивов (-).
3. Правую и левую скобки. {(,)} Скобки позволяют определять последовательность выполненияопераций в выражении.
Рассматриваемые изображения А1, А2 и А3 описываются на языке PDL соответственно следующими выражениями.
T(1)=R+((R-(L+N))*E-L
T(2)=(R+N)+((N+R)-L)*E-L
T(3)=(N+R)+(R-L)*E-(L+N)
После того как лингвистическое описание изображения построено, необходимо с помощью некоторой распознающей процедуры проанализировать, принадлежит или нет данное изображение к интересующему нас классу (классу букв А), т.е. обладает или нет это изображение некоторой структурой. Для этого прежде всего необходимо описать класс изображений, имеющих интересующую нас структуру.
Очевидно, буква А всегда содержит следующие структурные элементы: левую "ножку", правую "ножку" и головную часть. Назовем эти элементы соответственно STL, STR, TR.
Тогда на языке PDL класс символов А - SIMB A описывается выражением
SIMB A = STL + TR - STR
Левая "ножка" STL всегда есть цепочка элементов R и N, что можно записать так
STL ‑> R ¦ N ¦ (STL + R)¦(STL + N)
(STL есть символ R или N, или цепочка, полученная добавлением кисходной цепочке STL символов R или N)
Правая "ножка" STR всегда есть цепочка элементов L и N, что можно записать так , т.е.
STR ‑> L¦N¦ (STR + L)¦(STR + N)
Головная часть буквы - TR представляет собой замкнутый контур, составленный из элемента E и цепочек типа STL и STR.
На языке PDLструктура TR описывается выражением
TR ‑> (STL - STR) * E
Окончательно получим следующее описание класса букв А:
SIMB A ‑> (STL + TR - STR),
STL ‑> R¦N¦ (STL + R)¦(STL + N)
STR ‑> L¦N¦ (STR + L)¦(STR + N)
TR ‑> (STL - STR) * E
Процедура распознавания в данном случае может быть реализована следующим образом.
1. Выражение, соответствующее образу, сравнивается с эталоннойструктурой STL + TR - STR.
2. Каждому элементу структуры STL, TR, STR, если это возможно, т.е. если описание изображения сравнимо с эталоном, ставится в соответствиенекоторое подвыражение из выражения T(А). Например,
для А1: STL=R, STR=L, TR=(R-(L+N))*E
для А2: STL = R + N, STR = L, TR = ((N + R) - L) * E
для А3: STL = N + R, STR = L + N, TR = (R - L) * E 3.
Выражения STL, STR, TR сравниваются с соответствующими им эталонными структурами.
4. Если структура каждого выражения STL, STR, TR соответствует эталонной, делается вывод о принадлежности образа к классу букв А. Если на каком-либо из этапов 2, 3, 4 обнаруживается несоответствие структуры анализируемого выражения эталону, делается вывод о непринадлежности образа классу SIMB A. Сопоставление структур выражений может проводиться с помощью алгоритмических языков LISP, PLANER, PROLOG и других подобных им языков искусственного интеллекта.
В рассматриваемом примере все цепочки STL составлены из символов N и R, а цепочки STR из символов L и N, что соответствует заданной структуре этих цепочек. Структура TR в рассматриваемых образах также соответствует эталонной, т.к. состоит из "разности" цепочек типа STL, STR, "умноженной" на символ E.
Т.о., приходим к выводу о принадлежности рассматриваемых образов классу SIMB A.
Синтез нечеткого регулятора электропривода постоянного тока в среде «MatLab»
Синтез нечеткого регулятора с одним входом и выходом.
Проблема состоит в том, чтобы заставить привод точно следить за различными входными сигналами. Выработка управляющего воздействия осуществляется нечетким регулятором, в котором структурно можно выделить следующие функциональные блоки: фаззификатор, блок правил и дефаззификатор.
 Рис.4 Обобщенная функциональная схема системы с двумя лингвистическими переменными.
Рис.4 Обобщенная функциональная схема системы с двумя лингвистическими переменными.
 Рис.5 Принципиальная схема нечеткого регулятора с двумя лингвистическими переменными.
Рис.5 Принципиальная схема нечеткого регулятора с двумя лингвистическими переменными.
Алгоритм нечеткого управления в общем случае представляет собой преобразование входных переменных нечеткого регулятора в его выходные переменные с помощью следующих взаимосвязанных процедур:
1. преобразование входных физических переменных, получаемых от измерительных датчиков с объекта управления во входные лингвистические переменные нечеткого регулятора;
2. обработка логических высказываний, называемых лингвистическими правилами, относительно входных и выходных лингвистических переменных регулятора;
3. преобразование выходных лингвистических переменных нечеткого регулятора в физические управляющие переменные.
Рассмотрим сначала самый простой случай, когда для управления следящим электроприводом вводятся всего две лингвистические переменные:
«угол» - входная переменная;
«управляющее воздействие» - выходная переменная.
Синтез регулятора будем осуществлять в среде «MatLab» с помощью тулбокса «Fuzzy Logic». Он позволяет создавать системы нечеткого логического вывода и нечеткой классификации в рамках среды MatLab, с возможностью их интегрирования в Simulink. Базовым понятием Fuzzy Logic Toolbox является FIS-структура - система нечеткого вывода (Fuzzy Inference System). FIS-структура содержит все необходимые данные для реализации функционального отображения “входы-выходы” на основе нечеткого логического вывода согласно схеме, приведенной на рис. 6.
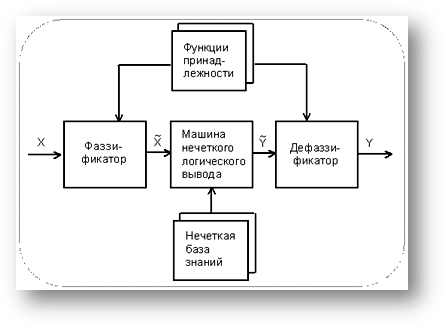
Рисунок 6. Нечеткий логический вывод.
X - входной четкий вектор; - вектор нечетких множеств, соответствующий входному вектору X;
- вектор нечетких множеств, соответствующий входному вектору X;
 - результат логического вывода в виде вектора нечетких множеств;Y - выходной четкий вектор.
- результат логического вывода в виде вектора нечетких множеств;Y - выходной четкий вектор.
Модуль fuzzy позволяет строить нечеткие системы двух типов - Мамдани и Сугэно. В системах типа Мамдани база знаний состоит из правил вида “Если x1=низкий и x2=средний, то y=высокий”. В системах типа Сугэно база знаний состоит из правил вида “Если x1=низкий и x2=средний, то y=a0+a1x1+a2x2". Таким образом, основное отличие между системами Мамдани и Сугэно заключается в разных способах задания значений выходной переменной в правилах, образующих базу знаний. В системах типа Мамдани значения выходной переменной задаются нечеткими термами, в системах типа Сугэно - как линейная комбинация входных переменных. В нашем случаем будем использовать систему Сугэно, т.к. она лучше поддается оптимизации.
Для управления следящим электроприводом, вводятся две лингвистические переменные: «ошибка» (по положению) и «управляющее воздействие». Первая из них является входной, вторая – выходная. Определим терм-множество для указанный переменных.
Основные компоненты нечеткого логического вывода. Фаззификатор.
Для каждой лингвистической переменной определим базовое терм-множество вида, включающее в себя нечеткие множества, которые можно обозначить: отрицательная высокая, отрицателная низкая, нуль, положительная низкая, положительная высокая.
Прежде всего субъективно определим что подразумевается под термами «большая ошибка», «малая ошибка» и т.д., определяя функции принадлежности для соответствующих нечетких множеств. Здесь пока можно руководствоваться только требуемой точностью, известными параметрами для класса входных сигналов и здравым смыслом. Никакого жесткого алгоритма для выбора параметров функций принадлежности пока никому предложить не удалось. В нашем случае лингвистическая переменная «ошибка» будет выглядеть следующим образом.
 Рис.7. Лингвистическая переменная «ошибка».
Рис.7. Лингвистическая переменная «ошибка».
Лингвистическую переменную «управление» удобнее представить в виде таблицы:
Таблица 1
| Функции принадлежности | Большое отрицательное UBO | Малое отрицательное UMo | Нулевое UZ | Малое положительное UMp | Большое положительное UBP |
| Значение управления, [В] | -27 | -15 | 0 | 15 | 27 |
Блок правил.
Рассмотрим последовательность определения нескольких правил, которые описывают некоторые ситуации:
Предположим, например, что выходной угол равен входному сигналу (т.е. ошибка - нуль). Очевидно, что это желаемая ситуация, и следовательно мы не должны ничего делать (управляющее воздействие - нуль).
Теперь рассмотрим другой случай: ошибка по положению сильно больше нуля. Естественно мы должны её компенсировать, формируя большой положительный сигнал управления.
Т.о. составлены два правила, которые могут быть формально определены так:
если ошибка = нуль, то управляющее воздействие = нуль.
если ошибка = большая положительная, то управляющее воздействие = большое положительное.
 Рис.8. Формирование управления при малой положительной ошибке по положению.
Рис.8. Формирование управления при малой положительной ошибке по положению.
 Рис.9. Формирование управления при нулевой ошибке по положению.
Рис.9. Формирование управления при нулевой ошибке по положению.
Ниже в таблице приведены все правила, соответствующие всем ситуациям для этого простого случая.
Таблица 2
| Ошибка по положению | |||||
| BO | Mo | Zero | Mp | BP | |
| Нечеткий сигнал управления | UBO | UMo | UZ | UMp | UBP |
Всего для нечеткого регулятора, имеющего n входов и 1 выход может быть определено  правил управления, где
правил управления, где  – количество нечетких множеств для i-го входа, но для нормального функционирования регулятора не обязательно использовать все возможные правила, а можно обойтись и меньшим их числом. В нашем случае для формирования нечеткого сигнала управления используются все 5 возможных правил.
– количество нечетких множеств для i-го входа, но для нормального функционирования регулятора не обязательно использовать все возможные правила, а можно обойтись и меньшим их числом. В нашем случае для формирования нечеткого сигнала управления используются все 5 возможных правил.
Дефаззификатор.
Таким образом, результирующее воздействие U будет определяться соответственно выполнению какого-либо правила. Если возникает ситуация, когда выполняются сразу несколько правил, то результирующее воздействие U находится по следующей зависимости:
 , где n-число сработавших правил (дефаззификация методом центра области), un – физическое значение управляющего сигнала, сответствующее каждому из нечетких множеств UBO, UMo, UZ, UMp, UBP. mUn(u) – степень принадлежности управляющего сигнала u к соответствующему нечеткому множеству Un={UBO, UMo, UZ, UMp, UBP}. Существуют также и другие методы дефаззификации, когда выходная лингвистическая переменная пропорциональна самомому «сильному» или «слабому» правилу.
, где n-число сработавших правил (дефаззификация методом центра области), un – физическое значение управляющего сигнала, сответствующее каждому из нечетких множеств UBO, UMo, UZ, UMp, UBP. mUn(u) – степень принадлежности управляющего сигнала u к соответствующему нечеткому множеству Un={UBO, UMo, UZ, UMp, UBP}. Существуют также и другие методы дефаззификации, когда выходная лингвистическая переменная пропорциональна самомому «сильному» или «слабому» правилу.
Промоделируем процесс управления электроприводом с помощью вышеописанного нечеткого регулятора.
 Рис.10. Структурная схема системы в среде Matlab.
Рис.10. Структурная схема системы в среде Matlab.

Рис.11. Структурная схема нечеткого регулятора в среде Matlab.

Рис.12. Переходный процесс при единичном ступенчатом воздействии.
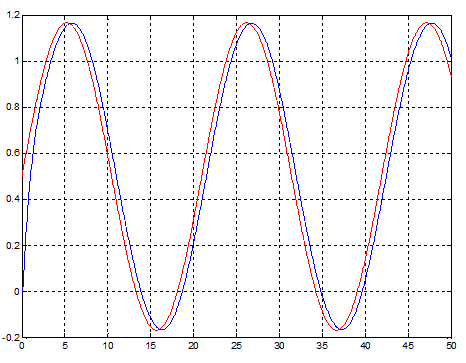
Рис. 13. Переходный процесс при гармоническом входном воздействии для модели с нечетким регулятором, содержащим одну входную лингвистическую переменную.
Анализ характеристик привода с синтезированным алгоритмом управления показывает, что они далеки от оптимальных и хуже, чем при синтезе управления другими методами (слишком большое время регулирования при единичном ступенчатом воздействии и ошибка при гармоническом). Объясняется это тем, что параметры функций принадлежности выбирались достаточно произвольно, а в качестве входов регулятора использовалась только величина ошибки по положению. Естественно ни о какой оптимальности полученного регулятора не может идти и речи. Поэтому актуальной становится задача оптимизации нечеткого регулятора, с целью достижения им максимально возможных показателей качества управления. Т.е. стоит задача оптимизации целевой функции f(a1,a2…an), где a1,a2…an – коэффициенты, определяющие вид и характеристики нечеткого регулятора. Для оптимизации нечеткого регулятора воспользуемся блоком ANFIS из среды Matlab. Также одним из способов улучшения характеристик регулятора может являться увеличение числа его входов. Это сделает регулятор более гибким и улучшит его характеристики. Добавим еще одну входную лингвистическую переменную – скорость изменения входного сигнала (его производную). Соответственно возрастет и число правил. Тогда принципиальная схема регулятора примет вид:

Рис.14 Принципиальная схема нечеткого регулятора с тремя лингвистическими переменными.
Пусть 
 - значение скорости входного сигнала. Базовое терм-множество Тn определим в виде:
- значение скорости входного сигнала. Базовое терм-множество Тn определим в виде:
Тn={”отрицательная (ВО)”, “нулевая (Z)”, ”положительная (ВР)”}.
Расположение функций принадлежности для всех лингвистических переменных показано на рисунке.
 Рис.15. Функции принадлежности лингвистической переменной «ошибка».
Рис.15. Функции принадлежности лингвистической переменной «ошибка».
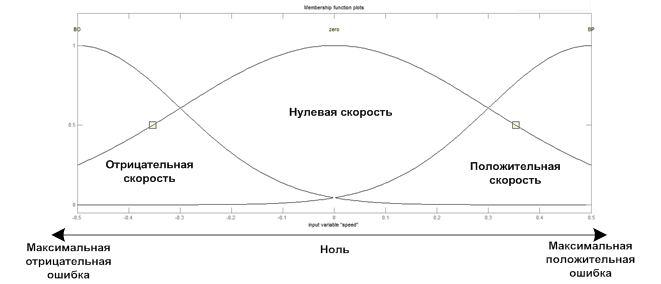
Рис.16. Функции принадлежности лингвистической переменной «скорость входного сигнала» .
В связи с добавлением еще одной лингвистической переменной, количество правил возрастет до 3x5=15. Принцип их составления полностью аналогичен рассмотренному выше. Все они приведены в следующей таблице:
Таблица 3
| Нечеткий сигнал управления | Ошибка по положению | |||||
| BO | MO | Z | MP | BP | ||
| Скорость | BP | BO | BO | MO | MP | BP |
| Z | BO | MO | Z | MP | BP | |
| BO | BO | MO | MP | BP | BP |
Например, если если ошибка = нуль, а производная входного сигнала = большая положительная, то управляющее воздействие = малое отрицательное.
 Рис.17. Формирование управления при трех лингвистических переменных.
Рис.17. Формирование управления при трех лингвистических переменных.
В связи с увеличением числа входов и соответственно самих правил, усложнится и структура нечеткого регулятора.
 Рис.18. Структурная схема нечеткого регулятора с двумя входами.
Рис.18. Структурная схема нечеткого регулятора с двумя входами.
Добавить рисунок
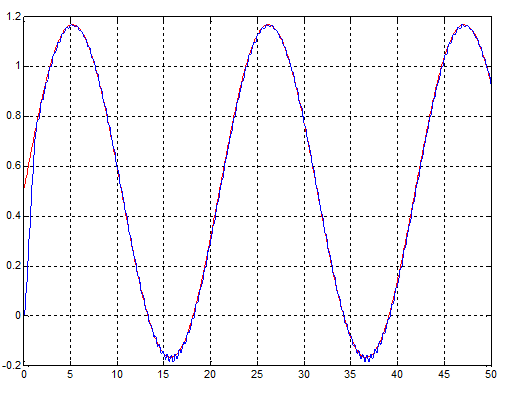
Рис.20. Переходный процесс при гармоническом входном воздействии для модели с нечетким регулятором, содержащим две входные лингвистические переменные.

Рис. 21. Сигнал ошибки при гармоническом входном воздействии для модели с нечетким регулятором, содержащим две входные лингвистические переменные.
Промоделируем работу нечеткого регулятора с двумя входами в среде Matlab. Структурная схема модели будет точно такой же, как на рис. 19. Из графика переходного процесса для гармонического входного воздействия можно видеть, что точность системы значительно возросла, но при этом увеличилась её колебательность, особенно в местах, где производная выходной координаты стремится к нулю. Очевидно, что причинами этого, как уже говорилось выше, является неоптимальный выбор параметров функций принадлежности, как для входных, так и для выходных лингвистических переменных. Поэтому оптимизируем нечеткий регулятор с помощью блока ANFISedit в среде Matlab.
Оптимизация нечеткого регулятора.
Рассмотрим использование генетических алгоритмов для оптимизации нечеткого регулятора. Генетические алгоритмы – адаптивные методы поиска, которые в последнее время часто используются для решения задач функциональной оптимизации. Они основаны на подобии генетическим процессам биологических организмов: биологические популяции развиваются в течении нескольких поколений, подчиняясь законам естественного отбора и по принципу "выживает наиболее приспособленный" (survival of the fittest), открытому Чарльзом Дарвином. Подражая этому процессу генетические алгоритмы способны "развивать" решения реальных задач, если те соответствующим образом закодированы.
Генетические алгоритмы работают с совокупностью "особей" - популяцией, каждая из которых представляет возможное решение данной проблемы. Каждая особь оценивается мерой ее "приспособленности" согласно тому, насколько "хорошо" соответствующее ей решение задачи. Наиболее приспособленные особи получают возможность "воспроизводить" потомство с помощью "перекрестного скрещивания" с другими особями популяции. Это приводит к появлению новых особей, которые сочетают в себе некоторые характеристики, наследуемые ими от родителей. Наименее приспособленные особи с меньшей вероятностью смогут воспроизвести потомков, так что те свойства, которыми они обладали, будут постепенно исчезать из популяции.
Так и воспроизводится вся новая популяция допустимых решений, выбирая лучших представителей предыдущего поколения, скрещивая их и получая множество новых особей. Это новое поколение содержит более высокое соотношение характеристик, которыми обладают хорошие члены предыдущего поколения. Таким образом, из поколения в поколение, хорошие характеристики распространяются по всей популяции. В конечном итоге, популяция будет сходиться к оптимальному решению задачи.
Имеются много способов реализации идеи биологической эволюции в рамках генетических алгоритмов. Традиционный, можно представить в виде следующей блок-схемы показанной на рисунке 22, где:
1. Инициализация начальной популяции – генерация заданного числа решений задачи, с которых начинается процесс оптимизации;
2. Применение операторов кроссовера и мутации;
3.  Условия останова – обычно процесс оптимизации продолжают до тех пор, пока не будет найдено решение задачи с заданной точностью, или пока не будет выявлено, что процесс сошелся (т.е. не произошло улучшения решения задачи за последние N поколений).
Условия останова – обычно процесс оптимизации продолжают до тех пор, пока не будет найдено решение задачи с заданной точностью, или пока не будет выявлено, что процесс сошелся (т.е. не произошло улучшения решения задачи за последние N поколений).
 В среде Matlab генетические алгоритмы представлены отдельным тулбоксом, а также пакетом ANFIS. ANFIS - это аббревиатура Adaptive-Network-Based Fuzzy Inference System - адаптивная сеть нечеткого вывода. ANFIS является одним из первых вариантов гибридных нейро-нечетких сетей - нейронной сети прямого распространения сигнала особого типа. Архитектура нейро-нечеткой сети изоморфна нечеткой базе знаний. В нейро-нечетких сетях используются дифференцируемые реализации треугольных норм (умножение и вероятностное ИЛИ), а также гладкие функции принадлежности. Это позволяет применять для настройки нейро-нечетких сетей быстрые и генетические алгоритмы обучения нейронных сетей, основанные на методе обратного распространения ошибки. Ниже описываются архитектура и правила функционирования каждого слоя ANFIS-сети.
В среде Matlab генетические алгоритмы представлены отдельным тулбоксом, а также пакетом ANFIS. ANFIS - это аббревиатура Adaptive-Network-Based Fuzzy Inference System - адаптивная сеть нечеткого вывода. ANFIS является одним из первых вариантов гибридных нейро-нечетких сетей - нейронной сети прямого распространения сигнала особого типа. Архитектура нейро-нечеткой сети изоморфна нечеткой базе знаний. В нейро-нечетких сетях используются дифференцируемые реализации треугольных норм (умножение и вероятностное ИЛИ), а также гладкие функции принадлежности. Это позволяет применять для настройки нейро-нечетких сетей быстрые и генетические алгоритмы обучения нейронных сетей, основанные на методе обратного распространения ошибки. Ниже описываются архитектура и правила функционирования каждого слоя ANFIS-сети.
ANFIS реализует систему нечеткого вывода Сугено в виде пятислойной нейронной сети прямого распространения сигнала. Назначение слоев следующее: первый слой - термы входных переменных; второй слой - антецеденты (посылки) нечетких правил; третий слой - нормализация степеней выполнения правил; четвертый слой - заключения правил; пятый слой - агрегирование результата, полученного по различным правилам.
Входы сети в отдельный слой не выделяются. На рис.23 изображена ANFIS-сеть с одной входной переменной («ошибка») и пятью нечеткими правилами. Для лингвистической оценки входной переменной «ошибка» используется 5 термов.
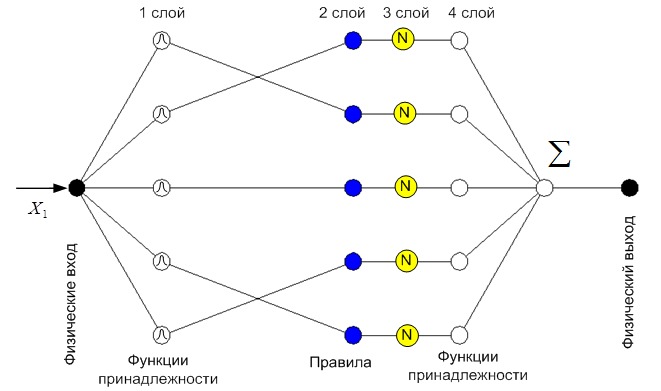
Рис.23. Структура ANFIS-сети.
Введем следующие обозначения, необходимые для дальнейшего изложения:
Пусть  - входы сети;
- входы сети;
y - выход сети;
 - нечеткое правило с порядковым номером r;
- нечеткое правило с порядковым номером r;
m - количество правил , ;
;
 - нечеткий терм с функцией принадлежности
- нечеткий терм с функцией принадлежности  , применяемый для лингвистической оценки переменной
, применяемый для лингвистической оценки переменной  в r-ом правиле (
в r-ом правиле ( ,
, );
);
 - действительные числа в заключении r-го правила (
- действительные числа в заключении r-го правила ( ,
, ).
).
ANFIS-сеть функционирует следующим образом.
Слой 1. Каждый узел первого слоя представляет один терм с колокообразной функцией принадлежности. Входы сети  соединены только со своими термами. Количество узлов первого слоя равно сумме мощностей терм-множеств входных переменных. Выходом узла являются степень принадлежности значения входной переменной соответствующему нечеткому терму:
соединены только со своими термами. Количество узлов первого слоя равно сумме мощностей терм-множеств входных переменных. Выходом узла являются степень принадлежности значения входной переменной соответствующему нечеткому терму:
 ,
,
где a, b и c - настраиваемые параметры функции принадлежности.
Слой 2. Количество узлов второго слоя равно m. Каждый узел этого слоя соответствует одному нечеткому правилу. Узел второго слоя соединен с теми узлами первого слоя, которые формируют антецеденты соответствующего правила. Следовательно, каждый узел второго слоя может принимать от 1 до n входных сигналов. Выходом узла является степень выполнения правила, которая рассчитывается как произведение входных сигналов. Обозначим выходы узлов этого слоя через  ,
,  .
.
Слой 3. Количество узлов третьего слоя также равно m. Каждый узел этого слоя рассчитывает относительную степень выполнения нечеткого правила:
 .
.
Слой 4. Количество узлов четвертого слоя также равно m. Каждый узел соединен с одним узлом третьего слоя а также со всеми входами сети (на рис. 18 связи с входами не показаны). Узел четвертого слоя рассчитывает вклад одного нечеткого правила в выход сети:
 .
.
Слой 5. Единственный узел этого слоя суммирует вклады всех правил:
 .
.
Типовые процедуры обучения нейронных сетей могут быть применены для настройки ANFIS-сети так как, в ней использует только дифференцируемые функции. Обычно применяется комбинация градиентного спуска в виде алгоритма обратного распространения ошибки и метода наименьших квадратов. Алгоритм обратного распространения ошибки настраивает параметры антецедентов правил, т.е. функций принадлежности. Методом наименьших квадратов оцениваются коэффициенты заключений правил, так как они линейно связаны с выходом сети. Каждая итерация процедуры настройки выполняется в два этапа. На первом этапе на входы подается обучающая выборка, и по невязке между желаемым и действительным поведением сети итерационным методом наименьших квадратов находятся оптимальные параметры узлов четвертого слоя. На втором этапе остаточная невязка передается с выхода сети на входы, и методом обратного распространения ошибки модифицируются параметры узлов первого слоя. При этом найденные на первом этапе коэффициенты заключений правил не изменяются. Итерационная процедура настройки продолжается пока невязка превышает заранее установленное значение. Для настройки функций принадлежностей кроме метода обратного распространения ошибки могут использоваться и другие алгоритмы оптимизации, например, метод Левенберга-Марквардта.
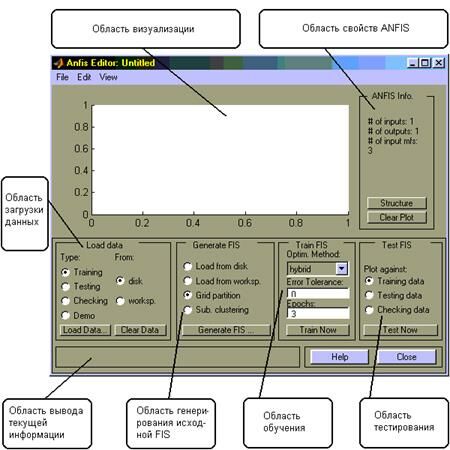
Рис.24. Рабочая область ANFISedit.
Попробуем теперь оптимизировать нечеткий регулятор для единичного ступенчатого воздействия. Желаемый переходный процесс имеет приблизительно следующий вид:
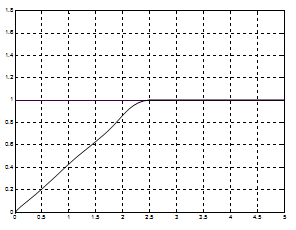
Рис.25. Желаемый переходный процесс.
Из графика изображенного на рис. следует, что большую часть времени двигатель должен работать на полную мощность, чтобы обеспечить максимальное быстродействие, а при приближении к желаемому значению должен плавно притормаживать. Руководствуясь этими простыми рассуждениями, в качестве обучающей возьмем следующую выборку значений, представленную ниже в виде таблицы:
Таблица 4
| Значение ошибки | Значение управления |
| 2 | 27 |
| 1 | 27 |
| 0.9 | 27 |
| 0.8 | 27 |
| 0.7 | 25 |
| 0.6 | 23 |
| 0.5 | 21 |
| 0.4 | 20 |
| 0.3 | 18 |
| 0.2 | 15 |
| 0.1 | 10 |
| Значение ошибки | Значение управления |
| 0.05 | 8 |
| 0.03 | 5 |
| 0.01 | 3 |
| 0.005 | 1 |
| 0.001 | 0.5 |
| 0 | 0 |
| -0.001 | -0.5 |
| -0.005 | -1 |
| -0.01 | -3 |
| -0.03 | -5 |
| -0.05 | -8 |
| Значение ошибки | Значение управления |
| -0.1 | -10 |
| -0.2 | -15 |
| -0.3 | -18 |
| -0.4 | -20 |
| -0.5 | -21 |
| -0.6 | -23 |
| -0.7 | -25 |
| -0.8 | -27 |
| -0.9 | -27 |
| -1 | -27 |
| -2 | -27 |
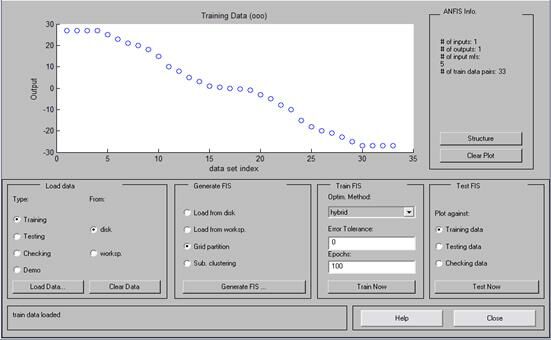
Рис.26. Вид обучающей выборки.
Обучение будем проводить на 100 шагах. Этого более чем достаточно для сходимости используемого метода.
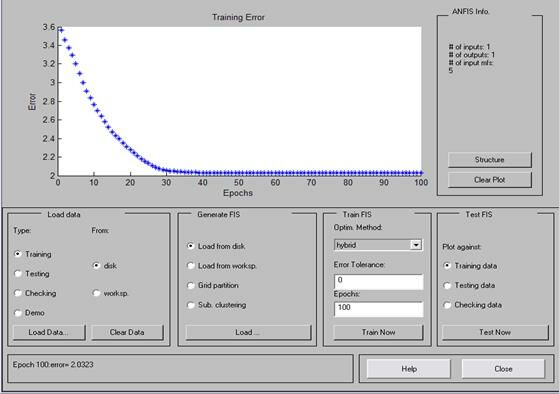
Рис.27. Процесс обучения нейросети.
В процессе обучения параметры функций принадлежности формируются таким образом, чтобы при заданной величине ошибки регулятор создавал необходимое управление. На участке между узловыми точками зависимость управления от ошибки является интерполяцией данных таблицы. Метод интерполяции зависит от способа обучения нейросети. Фактически после обучения модель нечеткого регулятора можно представить нелинейной функцией одной переменной, график которой представлен ниже.

Рекомендуем посмотреть лекцию "6 Способы обработки знаний".
Рис.28. График зависимости управления от ошибки поп положению внутри регулятора.
Сохранив найденные параметры функций принадлежности, промоделируем систему с оптимизированным нечетким регулятором.
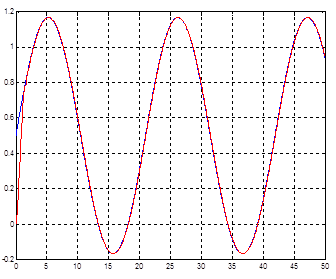
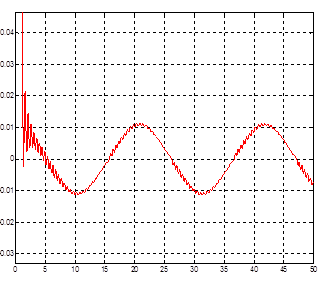
Рис. 29. Переходный процесс при гармоническом входном воздействии для модели с оптимизированным нечетким регулятором, содержащим одну входную лингвистическую переменную.
Рис.30. Сигнал ошибки при гармоническом входном воздействии для модели с нечетким регулятором, содержащим две входные лингвистические переменные.
Из графиков следует, что оптимизация нечеткого регулятора с помощью обучения нейросети удалась. Значительно снизилась колебательность и величина ошибки. Поэтому использование нейросети является вполне обоснованным для оптимизации регуляторов, принцип действия которых основан на нечеткой логике. Тем не менее, даже оптимизированный регулятор не может удовлетворить предъявленные требования по точности, поэтому целесообразно рассмотреть еще один способ управления, когда нечеткий регулятор управляет не непосредственно объектом, а занимается соединением нескольких законов управления в зависимости от сложившейся ситуации.






















