Магнитное поле движущихся зарядов. Закон Био-Савара-Лапласа

§ 3.2. Магнитное поле движущихся зарядов. Закон Био-Савара-Лапласа.

Результаты экспериментального исследования действия тока на магнитную стрелку были доложены на заседании Парижской Академии Био и Саваром 30 сентября 1820 г. В математическую форму элементарного взаимодействия между элементом тока и напряженностью поля в точке облек этот закон Лаплас.

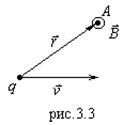
Постановка вопроса такова. Есть заряд , движущийся со скоростью . Он создает магнитное поле  (рис.3.3). Необходимо найти его величину в точке А. Экспериментально было установлено, что:

,                            (3.12)

где постоянная  зависит от системы единиц. Если , то:

                            -        (3.13)

закон Био-Савара-Лапласа. В законе - элемент длины проводника с током; 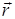- радиус-вектор точки, в которой измеряется магнитное поле .

         По принципу суперпозиции:

.                (3.14)

Рекомендуемые материалы

Заметим, что этот закон является своеобразным двойником закона Кулона в электростатике: напряженность поля обратно пропорциональна квадрату расстояния до точки наблюдения.

Примеры.

1. Определить магнитное поле проводника, по которому течет ток величины  (прямого тока) в точке, удаленной на расстояние от него  (рис.3.4). Воспользуемся (3.13), где угол:

.

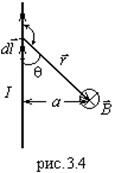
Вектор  направлен “от нас” в точке измерения.

.                  (3.15)

Так как      ;    ;  , то:

.               (3.16)

Силовые линии представляют собой окружности (направление определяется по правилу буравчика).

2. Определить величину магнитной индукции на оси витка с током в форме окружности радиуса . По витку течет ток  (рис.3.5).

По (3.13) векторы  направлены в точке оси z вдоль образующих конуса. Нормальные компоненты вектора ‑ его проекции на направление, перпендикулярное оси z ‑ при суммировании взаимно скомпесируются, останутся лишь тангенциальные компоненты (проекции на ось z):

;

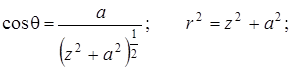
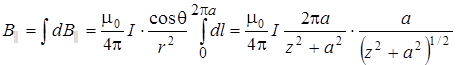
.                                   (3.17)

В центре витка:

.                               (3.18)

Зависимость  показана на рис.3.6.

При

,                         (3.19)

где  - магнитный момент витка. В СИ: [М]=А×м².

Виток, имеющий магнитный момент, создает на оси витка поле , перпендикулярное плоскости витка и совпадающее по направлению с моментом . В отличие от электрического поля кольца, по другую сторону витка вектор  не изменяет направление (см. для сравнения рис.1.4); направление  зависит лишь от направления тока (рис.3.6). Поэтому  - полярный вектор, а – аксиальный.

Общая формула для  в любой точке пространства с радиусом - вектором :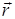

.                     (3.20)

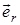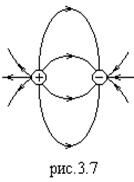
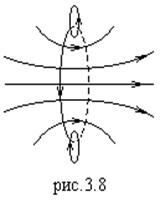
Здесь - единичный вектор вдоль 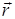. На рис.3.7 и 3.8. показаны силовые линии электрического диполя и витка с током. Видно, что поле витка с током во многом выглядит похожим на поле электрического диполя.

Поэтому Ампером было введено понятие “магнитного диполя”, который представлял собой виток с током, имеющий магнитный момент: .

3. Найти величину индукции магнитного поля соленоида длиной  с числом витков , по которому течет ток  (рис.3.9).

         В основу расчета положим формулу (3.17) для витка с током. Плотность намотки . На длине  течет ток . Начало отсчета - в центре соленоида.

Рекомендация для Вас - 20 Структура общества и брачно-семейные отношения.

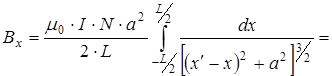
,    (3.21)

где  - координата точки, в которой измеряется индукция.

При            .             (3.22)

В центре соленоида    ,        где   .