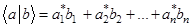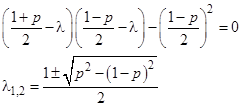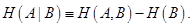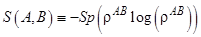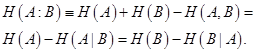Основные понятия квантовой теории информации (продолжение)
Лекция 5
II. Основные понятия квантовой теории информации (продолжение)
1. Энтропия фон Неймана, ее неотрицательность, максимальное значение. Квантовая относительная энтропия. Неравенство Клейна.
2. Композиционные системы. Субаддитивность и вогнутость энтропии. Энтропия смеси состояний. Совместная энтропия. Условная энтропия. Взаимная информация. Примеры. Различие между классической и квантовой информацией.
3. Достижимая информация.
4. Теорема о запрете клонирования квантовых состояний. Ее связь с достижимой информацией.
На прошлых лекциях было введено понятие классической (Шенноновской) и квантовой (фон Неймана) энтропий. Шенноновская энтропия (далее будем обозначать ее буквой H) дает меру неопределенности, связанную с классическим распределением вероятностей. Квантовые состояния описываются схожим образом, только вместо распределения вероятностей используются операторы плотности. Важно, что квантовые состояния могут быть неортоганальными. Мы определили энтропию фон Неймана квантового состояния r соотношением:
 (5.1)
(5.1)
Напомним, что в теории информации логарифмы принято брать по основанию “2” (а в статистической физике - по основанию “е” - “наты”).
Рекомендуемые материалы
Если lx - собственные значения матрицы плотности r, то выражение (5.1) для энтропии фон Неймана можно переписать по-другому:
 (5.2)
(5.2)
где, как обычно, считается, что 0 log0 T 0 (как и для Шенноновской энтропии). При вычислениях удобнее пользоваться последней формулой. Например, как было показано на прошлой лекции для полностью смешанного состояния в N-мерном пространстве энтропия равна logN.
Пример. Сравнение квантовой и классической энтропии. Вычислим энтропию смеси состояний
 . (Сравнить результат с Шенноновской энтропией H(p, 1-p) ). Приведенное состояние есть проектор (с вероятностью p) на состояние
. (Сравнить результат с Шенноновской энтропией H(p, 1-p) ). Приведенное состояние есть проектор (с вероятностью p) на состояние  или ( с вероятностью 1-p) на состояние
или ( с вероятностью 1-p) на состояние  .
.
Решение.
Учтем, что

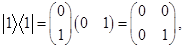

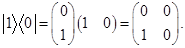
Тогда 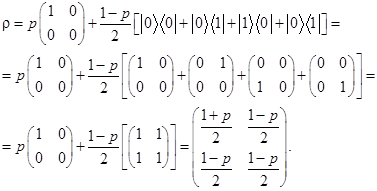
Ур-ие на собственные значения:
|
|
Пусть, например, p = 1/2. Тогда 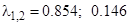
 .
.
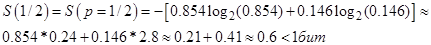
(Видно, что S, вычисленная из последней матрицы отличается от H(p, 1-p)).
Квантовая относительная энтропия.
Как и для энтропии Шеннона, полезно ввести квантовый аналог относительной энтропии. Пусть r и s -два оператора плотности. Относительная энтропия состояний (операторов) r и s (r относительно s) называется величина:
 (5.3)
(5.3)
Как и соответствующая классическая величина, квантовая относительная энтропия может принимать бесконечные значения.
Так, относительная энтропия определяется как бесконечная, если ядро (kernel) оператора s (векторное пространство собственных векторов s с нулевыми собственными значениями) имеет нетривиальное пересечение с основанием (support) оператора r (векторное пространство образованное собственными векторами r с ненулевыми собственными значениями). В других случаях относительная энтропия конечна.
Квантовая относительная энтропия неотрицательна (неравенство Клейна):
 (5.4)
(5.4)
равенство достигается, когда r = s.
Перечислим основные свойства энтропии фон Неймана.
1. Энтропия неотрицательна. Она принимает нулевые значения только для чистых состояний (доказательство следует из определения).
2. В N - мерном гильбертовом пространстве максимальное значение энтропии logN. Энтропия равна logN только если система находится в (полностью) смешанном состоянии I/N.
3. Предположим, что композиционная система AB находится в чистом состоянии. Тогда S(A) = S(B).
4. Предположим, что pi - это вероятности, а состояние r - раскладывается по собственным векторам с ненулевыми собственными значениями (имеют основание) в ортогональном базисе. Тогда
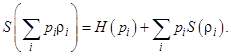
Док-во. Пусть  и
и  - собственные значения и собственные векторы состояния ri (в прошлой лекции было использовано инверсное обозначение верхних и индексов, но по-прежнему, i нумеровал классическую выборку, а j – собственные векторы). Видно, что
- собственные значения и собственные векторы состояния ri (в прошлой лекции было использовано инверсное обозначение верхних и индексов, но по-прежнему, i нумеровал классическую выборку, а j – собственные векторы). Видно, что  и
и  - собственные значения и собственные векторы состояния
- собственные значения и собственные векторы состояния  , поэтому
, поэтому
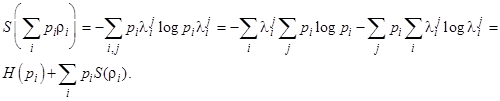
Видно, что если rI – чистые состояния, то 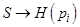
5. Теорема о совместной энтропии: Предположим, что pi - вероятности,  - ортогональные состояния для системы А и ri - любой набор операторов плотности для другой системы В, Тогда
- ортогональные состояния для системы А и ri - любой набор операторов плотности для другой системы В, Тогда
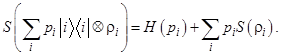
(Доказывается аналогично (4)).
6. Субаддитивность энтропии . Пусть различные квантовые системы А и В имеют общее состояние rАВ. Тогда совместная энтропия для двух систем удовлетворяет следующим неравенствам:
 - причем равенство имеет место только если системы А и В некоррелированы, т.е.
- причем равенство имеет место только если системы А и В некоррелированы, т.е. 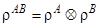
 - т.н. неравенство треугольника или Араки-Льеба. Это, фактически, квантовый аналог неравенства
- т.н. неравенство треугольника или Араки-Льеба. Это, фактически, квантовый аналог неравенства  для энтропии Шеннона.
для энтропии Шеннона.
7. Вогнутость энтропии. Пусть pi - неотрицательные действительные числа, такие, что  , а ri - соответствующие операторы плотности. Тогда энтропия удовлетворяет неравенству:
, а ri - соответствующие операторы плотности. Тогда энтропия удовлетворяет неравенству:
 - следует из св-ва (4).
- следует из св-ва (4).
Интуитивно ясно, что  выражает состояние квантовой системы, которая находится в неизвестном состоянии ri с вероятностью pi. Неопределенность нашего знания о такой смеси состояний должна быть больше, чем средняя неопределенность состояний ri, поскольку состояние
выражает состояние квантовой системы, которая находится в неизвестном состоянии ri с вероятностью pi. Неопределенность нашего знания о такой смеси состояний должна быть больше, чем средняя неопределенность состояний ri, поскольку состояние  дает вклад в неопределенность не только из-за наличия состояний ri но и благодаря усреднению по индексу i.
дает вклад в неопределенность не только из-за наличия состояний ri но и благодаря усреднению по индексу i.
8. Энтропия смеси квантовых состояний. Обратная сторона условия вогнутости проявляется в некоей полезной теореме, дающей верхнюю границу для энтропии смеси квантовых состояний. А именно, что для смеси  квантовых состояний ri выполняется следующее неравенство:
квантовых состояний ri выполняется следующее неравенство:
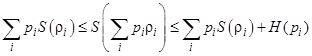
Что можно сказать о верхней границе или о правой части неравенства? Интуитивно ясно, что неопределенность состояния  не может быть больше, чем средняя неопределенность состояния ri плюс дополнительный вклад за счет H(pi), который представляет собой максимально возможный вклад в неопределенность об индексе i в общую неопределенность. Сформулируем теперь теорему о верхней границе
не может быть больше, чем средняя неопределенность состояния ri плюс дополнительный вклад за счет H(pi), который представляет собой максимально возможный вклад в неопределенность об индексе i в общую неопределенность. Сформулируем теперь теорему о верхней границе
Теорема. Предположим, что  , где pi - некоторый набор вероятностей, а ri - операторы плотности. Тогда
, где pi - некоторый набор вероятностей, а ri - операторы плотности. Тогда
 , (**)
, (**)
причем равенство достигается, если состояния ri образуют ортогональный набор.
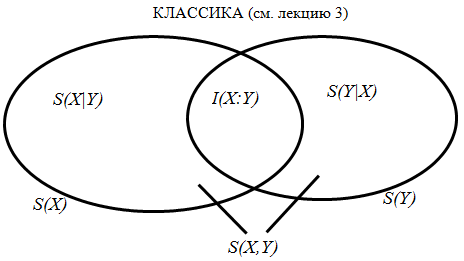
По аналогии с классическим случаем (энтропия Шеннона) для композиционных систем можно определить квантовые совместную и условную энтропии, а также квантовую взаимную информацию. Совместная энтропия S(A, B) для композиционной системы, состоящей из двух компонент А и В, определяется как и в классике:
 (5.5)
(5.5)
где  - матрица плотности системы АВ. Напоминание:
- матрица плотности системы АВ. Напоминание:
в классике условной энтропией называлась величина
 , (+)
, (+)
где во втором равенстве использовано понятие совместной вероятности
 - есть вероятность того, что Х принимает значение х, а Y принимает значение y.
- есть вероятность того, что Х принимает значение х, а Y принимает значение y.
Из определения (+) следует, что S(Y|X) есть мера того, сколько информации, в среднем, оставалось бы в Y при условии, что мы бы знали Х. Заметим, что всегда S(Y|X) _ S(Y) и обычно S(Y|X) _ S(Х|У). (конец напоминания)
Определим условную энтропию, как
 (5.6)
(5.6)
Определим взаимную информацию, как
 (5.7)
(5.7)
Некоторые свойства энтропии Шеннона не переносятся на энтропию фон Неймана и отсюда следуют интересные следствия квантовой теории информации. Например, для случайных переменных X и Y имеет место неравенство: H(X) _ H(X, Y). Интуитивно, это понятно: не может быть большей неопределенности состояния X, чем для совместного состояния X и Y. Это интуитивное понимание не годится для квантовых состояний. Рассмотрим систему АВ двух кубитов в перепутанном состоянии :
 . (*)
. (*)
Это чистое состояние, поэтому S(A, B) = 0. С другой стороны, система А имеет оператор плотности I/2 (I - единичный оператор) и поэтому ее энтропия равна единице. Действительно, волновой функции состояния системы А (или В)(*) не существует, это состояние максимально смешанное. Другой способ озвучивания этого результата состоит в том, что для этой системы величина (условная энтропия)  - отрицательная. Это соотношение может трактоваться как критерий перепутывания: Если |АВ> - чистое состояние композиционной системы, то |АВ> находится в перепутанном состоянии если и только если S(A|B) < 0.
- отрицательная. Это соотношение может трактоваться как критерий перепутывания: Если |АВ> - чистое состояние композиционной системы, то |АВ> находится в перепутанном состоянии если и только если S(A|B) < 0.
 (12.5)
(12.5)
Тогда
 , (12.6)
, (12.6)
т.е. представляет собой взвешенную смесь. Следовательно, состояние второй подсистемы нельзя описывать волновой функцией; оно не является полностью определенным. Аналогично, матрица плотности первой подсистемы находится как след по индексам второй подсистемы:
 . (12.7)
. (12.7)
Классическая теория информации, в основном, затрагивает проблему пересылки классических сообщений - букв алфавита, текстов, строк битов - через каналы связи, которые работают в соответствии с законами классической физики. Как изменится картина, если будут использоваться квантовые каналы связи? Можно ли передать информацию более эффективно? Можно ли использовать законы квантовой механики для того, чтобы передавать секретную информацию, защищенную от подслушивания? Такого рода вопросы возникают, когда мы используем каналы связи, работающие по законам квантовой механики. Такое переопределение того, что же есть канал связи вызвано необходимостью переосмысления основных положений классической теории информации .
Квантовая теория информации нацелена на исследование каналов связи, но она имеет гораздо более широкую область применения. Можно обозначить три фундаментальные цели, которые стоят перед теорией квантовой информации:
n идентифицировать элементарные классы статических ресурсов в квантовой механике (или типы “информации”)
n идентифицировать элементарные классы динамических процессов в квантовой механике ( или типы информационных процессов)
n характеризовать ресурсы, с помощью которых можно реализовать элементарные динамические процессы.
Оказывается, что квантовая теория информации гораздо глубже и богаче классической теории информации потому, что квантовая механика включает в себя гораздо больше элементарных классов статических и динамических ресурсов, которые не просто соответствуют известным классическим типам, но и описывают целые новые типы состояний, например, перепутанные состояния, которые не имеют аналога в классике.
Рассмотрим на некоторых примерах разницу в описании между квантовой и классической информацией.
Принцип соответствия. “Законы квантовой физики должны быть сформулированы таким образом, что в классических границах, когда в процесс вовлечено много квантов, эти законы приводили бы к классическим уравнениям для усредненных величин.” (Д.Бом. Квантовая теория)
Предположим, что Алиса имеет классический источник информации, который выдает символы X = 0, ... n с соответствующим распределением вероятностей p0, ..., pn. Цель Алисы и Боба состоит в том, чтобы Боб смог определить величину X наилучшим образом. Для того, чтобы достигнуть этого. Алиса приготавливает квантовое состояние rХ выбирая его из некоторого фиксированного набора r0,.... rn, и посылает это состояние Бобу, который выполняет квантовое измерение над этим состоянием. Затем, он пытается сделать лучшее предположение о том, как идентифицировать X, основываясь над результатах своих измерений Y.
Хорошей мерой того, сколько информации получено Бобом о величине X из его измерений - это взаимная информация между X и результатом измерения Y. Мы помним из предыдущих лекций, что Боб может сделать заключение об X по результатам измерения Y только, если и только если H(X:Y) = H(X), и что в общем случае H(X:Y) _ H(X). Далее мы покажем, что близость величины H(X:Y) к H(X) не самом деле дает хорошую меру того, как Боб смог определить Х. Цель Боба - выбрать измерение, которое максимизирует величину H(X:Y) и тем самым приближая ее к H(X). Для этого, определим достижимую информацию (accessible information), как максимальную величину взаимной информации. Достижимая информация - это мера того, насколько хорошо Боб смог сделать вывод о приготовленном Алисой состоянии, которая она послала ему.
| Квантовая информация | Классическая информация |
| Условная энтропия:
МОЖЕТ БЫТЬ ОТРИЦАТЕЛЬНОЙ!! | Условная энтропия:
H(B|A) Ј H(B) |
| Совместная энтропия:
| Совместная энтропия: H(A), H(B) _ H(B,A) |
| Взаимная информация:
| Взаимная информация:
|
В теории классической информации, достижимая информация не так интересна. Если на практике различение пары классических состояний может встретить определенные трудности, то в принципе, это всегда можно проделать. В отличие от этого, в квантовом случае, далеко не всегда возможно различить два состояния даже в принципе. Например, не существует однозначной процедуры, позволяющей различить два неортогональных состояния. Будем “выражаться” в терминах достижимой информации. Если Алиса готовит состояние 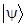 с вероятностью p и другое неортогональное состояние
с вероятностью p и другое неортогональное состояние 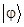 с вероятностью 1 - p, то достижимая информация при таком приготовлении уж точно меньше, чем H(p), поскольку Боб не может определить принадлежность состояния с полной достоверностью. В классике - если Алиса готовит два классических состояния, например, бит - в состоянии “0” с вероятностью p или “1” с вероятностью 1 - p, то не существует фундаментального закона, запрещающего Бобу различить эти состояния; поэтому достижимая информация оказывается такой же как и энтропия приготовления, т.е. H(p).
с вероятностью 1 - p, то достижимая информация при таком приготовлении уж точно меньше, чем H(p), поскольку Боб не может определить принадлежность состояния с полной достоверностью. В классике - если Алиса готовит два классических состояния, например, бит - в состоянии “0” с вероятностью p или “1” с вероятностью 1 - p, то не существует фундаментального закона, запрещающего Бобу различить эти состояния; поэтому достижимая информация оказывается такой же как и энтропия приготовления, т.е. H(p).
Существует важное замечание, относящееся к этой дискуссии - когда концепция достижимой информации имеет классический смысл. Суть его - в различении распределений вероятностей. Представим, что Алиса готовит состояние “0” или “1” с двумя распределениями вероятностей либо с (p, 1 - p) либо с (q, 1 - q). Получая состояние Боб должен определить, какое распределение вероятности использовала Алиса для приготовления состояния. Очевидно, что Боб не всегда способен определить это с достоверностью 100%. Тем не менее, этот пример (по аналогии с достижимой информацией для квантовой системы, приготавливаемой в одном состоянии из набора смешанных состояний) очень важен. Что является наиболее важным и замечательным - так это то, что фундаментальные объекты в квантовой механике - чистые квантовые состояния - обладают свойствами различимости, что является существенно отличным и существенно богатым свойством, нежели чем для фундаментальных объектов классической теории информации, таких как “0” и “1”.
Теорема о запрете копирования (клонирования)
Теорема о запрете клонирования сулит другую перспективу в плане ограничения на достижимую квантовую информацию, по сравнению с классической. Классическая информация, безусловно, может быть копирована. Это точно можно сделать с цифровой информацией, например. создавая копии файлов с текстами, заложенными в компьютер. Теорема о запрете клонирования утверждает, что квантовая механика не позволяет точно копировать неизвестное квантовое состояние и накладывает некоторые ограничения на возможность создания примерных копий.
На первый взгляд, теорема о запрете клонирования выглядит довольно странно. В конце концов, не является ли классическая физика частным случаем квантовой механики? Почему мы можем копировать классическую информацию, если нельзя копировать квантовую? Ответ состоит в том, что эта теорема не запрещает копировать все квантовые состояния. Она лишь утверждает, что нельзя копировать неортогональные квантовые состояния. Далее, теорема подразумевает, что невозможно построить квантовый прибор так, что бы при наличии на входе состояний  и
и 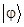 , на выходе будет две копии входного состояния
, на выходе будет две копии входного состояния 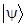
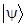 или
или 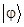
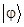 . С другой стороны, если
. С другой стороны, если 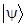 и
и 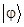 ортогональны, то теорема не запрещает их копирование. Действительно, довольно просто сконструировать квантовые схемы, которые копируют такие состояния. Это замечание разрешает кажущееся противоречие между теоремой о запрете клонирования и способностью копировать классическую информацию. Для различных состояний классическая информация может восприниматься как представляемая ортогональными состояниями!
ортогональны, то теорема не запрещает их копирование. Действительно, довольно просто сконструировать квантовые схемы, которые копируют такие состояния. Это замечание разрешает кажущееся противоречие между теоремой о запрете клонирования и способностью копировать классическую информацию. Для различных состояний классическая информация может восприниматься как представляемая ортогональными состояниями!
Доказательство теоремы.
Предположим, что у нас есть квантовое устройство с двумя портами (slots), обозначенными А и В. Порт А - это порт данных. В него помещается неизвестное, но чистое квантовое состояние 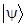 . Это состояние требуется скопировать на порте В - это т.н. порт - мишень. Предположим, что порт - мишень изначально находится в некоем стандартном чистом состоянии
. Это состояние требуется скопировать на порте В - это т.н. порт - мишень. Предположим, что порт - мишень изначально находится в некоем стандартном чистом состоянии  .Таким образом, начальное состояние всего копирующего устройства есть:
.Таким образом, начальное состояние всего копирующего устройства есть:
 . (5.8)
. (5.8)
Процедура копирования подвергается некоторой унитарной эволюции U. В идеальном случае
 (5.9)
(5.9)
Предположим, что процедура копирования работает для каких-нибудь двух особых чистых состояний 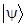 и
и 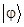 . Тогда,
. Тогда,
 (5.10)
(5.10)
 (5.11)
(5.11)
Находя скалярное (= внутреннее) произведение этих двух уравнений, получаем, что
Бесплатная лекция: "10 Гнойная инфекция - актуальная проблема хирургии" также доступна.
Унитарность дает  , а раскрывая прямое произведение векторов, и учитывая, что
, а раскрывая прямое произведение векторов, и учитывая, что  получаем:
получаем:
 (5.12)
(5.12)
Но уравнение х2 = х имеет только два решения: х = 0 и х = 1, поэтому 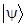 =
= 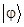 или
или 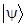 и
и 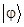 - ортогональны! Следовательно, копирующее устройство может копировать только состояния ортогональные друг другу. Отсюда - в общем случае квантовые состояния нельзя копировать (клонировать). Например, квантовый клонер не может клонировать состояния кубита
- ортогональны! Следовательно, копирующее устройство может копировать только состояния ортогональные друг другу. Отсюда - в общем случае квантовые состояния нельзя копировать (клонировать). Например, квантовый клонер не может клонировать состояния кубита 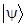 = 0 и
= 0 и  т.к. эти состояния неортогональны.
т.к. эти состояния неортогональны.
Напоминание.
Прямым (внешним) произведением двух векторов  и
и  называется вектор, размерности
называется вектор, размерности  вида
вида  .
.
Скалярным (внутренним) произведением векторов называется число