Связь между характеристиками упругости свойств материала E, G, мю
Связь между характеристиками упругости свойств материала E,G,мю.
Расчёт на прочность при изгибе:
σmax ≤ [σ] ≤ στ / nτ ,где σmax = Mx max / Wx
| НАПРЯЖЕНИЕ ПРИ ИЗГИБЕ И РАСЧЕТ БРУСЬЕВ НА ПРОЧНОСТЬ |
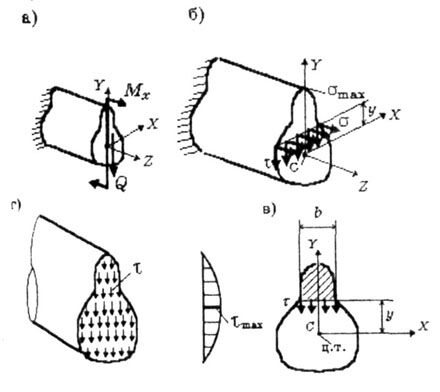
| Во всех точках поперечного сечения бруса при поперечном изгибе возникают нормальные и касательные напряжения (на рис. 5.1,6 эти напряжения показаны в точках, отстоящих на расстоянии Y от оси X): |
|
|
| Рис. 5.1 |
| Условные обозначения. |
| Mx, Q - внутренние усилия: изгибающий момент и поперечная сила, они изменяются вдоль бруса и определяются с помощью построения эпюр; |
Рекомендуемые материалыВ многоходовом горизонтальном кожухотрубчатом теплообменнике нагревается жидкость от температуры t2н,ºС до температуры t2к, ºС. Расход жидкости – G, кг/ч. Греющий теплоноситель – водяной насыщен-ный пар давлением Pн, бар. Размеры труб: на Один моль одноатомного идеального газа совершает в тепловой машине цикл Карно между тепловыми резервуарами с температурами 400 К и 300 К. Наименьший объем газа в ходе цикла 5 л, наибольший объем 20 л. Какую работу совершает эта машина за один цикл? С Элементы цепи, схема которой изображена на рис. 3.9, имеют следующие значения: e1 = 2 В, e2 = 3 В, R1 = 3 кОм, R2 = 2 кОм. Определить показание вольтметра, если его внутреннее сопротивление 5 кОм. Внутренними сопротивлениями источников тока пренебреч Газовая смесь G, заданная объемными долями и занимающая исходный объем V1, нагревается при постоянном давлении от температуры t1 до температуры t2, а потом охлаждается при постоянном объеме до исходной температуры t1. Определить конечное давление и о При освещении металла монохроматическим светом с частотой ν∙10-15=1,207 Гц задерживающий потенциал оказался равным U3=0,750 В . Найти: а) длину волны, энергию, массу, импульс, фотона, падающего на металл; б) кинетическую энергию e и скорость фотоэл FREE Волновые свойства света у - координата точек поперечного сечения, в которых определяются напряжения; |
| b - ширина сечения в месте определения касательных напряжений; |
| Jx - главный центральный момент инерции -момент инерции относительно центральной оси х, |
| сx* - статический момент относительно нейтральной оси ж той части площади поперечного сечения, которая расположена выше (или ниже) продольного сечения - выше или ниже уровня у, в точках которого определяются касательные напряжения. |
|
|
| Эти формулы выведены в главных центральных осях поперечного сечения бруса. На рис. 5.1 это оси X, У. При этом ось Y совпадает с осью симметрии сечения, а ось X, перпендикулярная плоскости изгиба, проходит через центр тяжести сечения и является нейтральной осью: нормальные напряжения в точках этой оси равны нулю. Ось Z - ось бруса. |
| Таким образом, на уровне у напряжения, определяемые вышеприведенными формулами, постоянны, не зависят от координаты X. |
| С увеличением координаты у нормальные напряжения увеличиваются и в наиболее удаленных от нейтральной оси точках достигают наибольшего значения: |
|
|
| Для расчетов используется специальная геометрическая характеристика - момент сопротивления сечения при изгибе: |
|
|
| Касательные напряжения, наоборот, уменьшаются и в наиболее удаленных от нейтральной оси точках обращаются в нуль, а а области нейтральной оси достигают наибольших значений (рис. 5.1,г). Кроме того, наибольшие значения касательных напряжений значительно меньше максимальных значений нормальных напряжений: так для консольного стержня прямоугольного поперечного сечения, нагруженного сосредоточенной силой на свободном конце, отношение максимальных значений этих напряжений |
| Информация в лекции "Групповые и индивидуальные формы работы" поможет Вам.
|
| где l, h - длина бруса и высота его поперечного сечения. |
| Поэтому, при l >> h, что имеет место в большинстве случаев, касательные напряжения по сравнению с нормальными пренебрежимо малы и при расчетах на прочность не учитываются. |
| Условие прочности имеет следующий вид: |
|
|
|
|
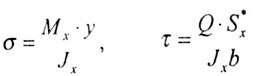
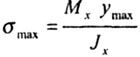
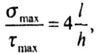
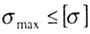
- допускаемое напряжение. 
