РАБОТА И ЭНЕРГИЯ

 Работа силы

                               Элементарная работа

Предположим, что точка приложения переменной по модулю и направлению силы перемещается по криволинейной траектории. Чтобы вычислить работу силы на этом перемещении, нужно разбить это перемещение на элементарные участки, вычислить работу силы на каждом элементарном участке, как работу постоянной силы, и определить предел суммы элементарных работ при стремлении числа участков к бесконечности и длины каждого из них к нулю.

Элементарная работа силы на участке dl определяется по формуле:

              (1),

где - импульс.

Элементарную работу обозначают , а не , так как в общем случае она не является дифференциалом функции. Знак работы определяется только знаком косинуса угла  – угла между векторами  и . Если  < , то работа силы положительна, если  > – отрицательна, а если  = , то работа силы равна 0.

Полная работа

Рекомендуемые материалы

        Полная работа на участке dl равна алгебраической сумме элементарных работ на отдельных бесконечно малых участках и сводится к интегралу

;

                                                     (2)
Для вычисления работы нужно:

1. Указать силу, с которой выполняется работа.

2. Определить перемещение, на котором выполняется эта работа, и угол между вектором перемещения и вектором силы.

Единицей измерения работы является джоуль (1 Дж). 1 Дж – работа, совершаемая силой 1 Н на пути 1 м (1 Н = 1 Н×м).

Пример 1.

Точка прошла 1/4 окружности. Найти работу.

Решение.

;

Пример 2.

Посчитать работу гравитационной силы.

;

;

Пример 3.

Посчитать работу силы упругости.

Пример 4.

Посчитать работу силы трения.

_тртртр

_тр

Мощность

Мощность силы – изменение работы силы, отнесенное к единице времени.

Если в течение малого промежутка времени dt сила  совершает  работу , то мощность этой силы

                                                                                          (3)

Таким образом, мощность силы равна скалярному произведению векторов силы и скорости ее точки приложения.

За единицу мощности в системе МКС принимается 1 ватт (Вт) = 1Дж/с.

Потенциальные (консервативные) силы

Все силы, действующие на частицы, можно разбить на две группы: потенциальные и непотенциальные. Силы называются потенциальными, если их работа при изменении положения частиц не зависит от формы пути при перемещении частиц, а определяется начальной и конечной конфигурациями системы. Это силы, зависящие от координат точек системы. Работа, выполняемая этими силами, не зависит от траектории движения, а зависит от начального и конечного положения. На замкнутой траектории работа потенциальных сил равна нулю. Это математическое правило.

, где - интеграл по замкнутому контуру.

Чтобы проверить, является ли сила потенциальной, нужно взять интеграл по замкнутому кругу.

Примеры потенциальных сил:

1)

2)

3)

4) Однородное поле сил

5) Центральное поле сил:

 

Работа непотенциальных сил зависит от формы пути. Примером таких сил является сила трения. 

Кинетическая и потенциальная энергии

Кинетическая энергия

Кинетическая энергия механической системы – это энергия механического движения этой системы.

Теорема о кинетической энергии.

                                                                                                 (1),

где  - кинетическая энергия (энергия движения), она всегда положительная.

Работа, выполняемая в системе любыми силами, равна разности кинетических энергий между конечным и начальным положением.                 

Потенциальная энергия

Потенциальная энергия – некоторая функция, которая зависит только от координат точек системы, всякое изменения которой, взятое с обратным знаком, равно работе консервативных сил, действующих на точки системы:

U=f(x; y; z).

Потенциальная энергия системы в любом данном ее положении равна сумме работ сил потенциального поля, приложенных к ее точкам на перемещении из данного положения в нулевое.

                                                                                                       (2)

                                                                                                        (3)

Знак «минус» указывает, что в результате выполнения работы потенциальными силами, энергия уменьшается.

Закон сохранения механической энергии

При движении механической системы под действием сил, имеющих потенциал, изменения кинетической энергии системы определяются зависимостями:

;   

                                                                                              (4),

где потенциальные энергии системы в 1 и 2 положениях.

Сумму кинетической и потенциальной энергий системы называют полной механической энергией системы.

                               

                        

По теореме о кинетической энергии:

 (5)

Таким образом, в замкнутой системе, в которой действуют только потенциальные силы, полная механическая энергия с течением времени не изменяется при любых процессах, происходящих внутри системы.

Пример.

Тело бросают вертикально вверх с начальной скоростью v₀. Найти высоту, на которой кинетическая и потенциальная энергии тела будут равны.

Решение.

Закон сохранения полной энергии

По теореме о кинетической энергии:

В реальных условиях на механическую систему могут действовать не только потенциальные силы, и полная механическая энергия системы может изменяться. Это происходит, когда часть энергии механической системы расходуется на преодоление различных сопротивлений или наблюдается приток энергии от других систем.

Расход механической энергии движущейся механической системы обычно означает превращение ее в теплоту, электричество, звук или свет, а приток механической энергии связан с обратным процессом превращения различных видов энергии в механическую энергию.

Таким образом, энергия не возникает и не исчезает бесследно, происходит только превращение одного вида энергии в другой в разных количествах, поэтому полная энергия системы с течением времени сохраняется при любых взаимодействиях внутри неё.

Работа, выполняемая непотенциальными силами, равна разности полной механической энергии между конечным положением и начальным.

Закон сохранения энергии для системы материальных точек

Предположим, что силы взаимодействия (F_вз) между частичками системы  - потенциальные силы.

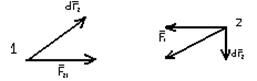
-для замкнутой системы материальных частиц.

Рассмотрим случай, когда на систему действуют потенциальные силы . Изменение .

    

                                                                                                  (1)

е

 явным образом не зависит от времени.

На частички некоторой системы действуют ещё и диссипативные силы, совершающие работу  часть  будет превращаться в другие виды энергии.

Если умножить на , то диссипативная сила даст

Энергия материальной точки в релятивистском случае и закон сохранения энергии в этом случае.

В релятивистском случае масса частиц зависит от n:

– умножим обе части равенства на v и т.к.

Покажем, что при малых v формула

           Безмассовые частицы – частицы у которых  и они движутся со скоростью света, например фотоны, для них:

 

Найдём связь между E и p:

Информация в лекции "63. Культурная адаптация работников" поможет Вам.

– инвариантная величина