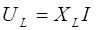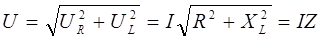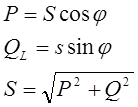Однофазные электрические цепи синусоидального тока (продолжение)
ЛЕКЦИЯ 5
Однофазные электрические цепи синусоидального тока (продолжение)
Электрическая цепь с R- элементом
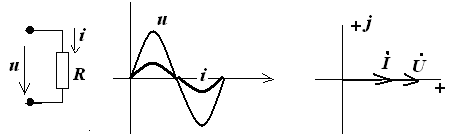
Рис.1
Рассмотрим схему с R-элементом, как показано на рис.1. Расставим направления тока и напряжения и запишем уравнения электрического состояния этой схемы согласно закону Ома:
i = u/R=(Um/R)sin(ωt+ ψu)= Imsin(ωt+ψi)
очевидно, что Um= RIm; ψu= ψi,
тогда угол сдвига фаз между напряжением и током будет равен 0, т.е. φ = ψu - ψi = 0, что и соответствует временной диаграмме показанной на рис.1 , напряжение и ток совпадают по фазе.
Рекомендуемые материалы
Для действующих значений закон Ома: U = RI
|
| комплексное сопротивление резистивного элемента является всегда действительным положительным числом, которое равно значению активного сопротивления R. |
Мощность на R- элементе:
 R = Р ± jQ угол сдвига фаз φ = 0, тогда Р = UIcosφ = UI, Q = UIsinφ = 0, следовательно на резистивном элементе полная мощность равна активной мощности. Это означает, что на резисторе совершается работа по преобразованию электрической энергии в тепловую.
R = Р ± jQ угол сдвига фаз φ = 0, тогда Р = UIcosφ = UI, Q = UIsinφ = 0, следовательно на резистивном элементе полная мощность равна активной мощности. Это означает, что на резисторе совершается работа по преобразованию электрической энергии в тепловую.
 R =Р
R =Р
Электрическая цепь с емкостным С - элементом
Идеальный конденсатор, когда его активное сопротивление Rc = 0.
|
| u(t)=Um sin(ωt+ ψu) i = i = C·ω·Umsin(ωt+ ψu+900) |
начальная фаза тока ψi = ψu + 90о
Из векторной диаграммы видно, что ток на конденсаторе опережает напряжение на 900
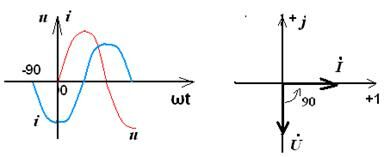
 , так как φ = -90о, то Z = Z·cos(-90о) + jZ·sin(-90о)= -jZ, а модуль комплексного сопротивления
, так как φ = -90о, то Z = Z·cos(-90о) + jZ·sin(-90о)= -jZ, а модуль комплексного сопротивления  , следовательно, сопротивление конденсатора чисто реактивное и равно:
, следовательно, сопротивление конденсатора чисто реактивное и равно:  .
.
Закон Ома: U=I·(-Xc)
Мощность на C – элементе:  c = Р ± jQ , угол сдвига фаз φ = -90о, тогда Р = UIcosφ = 0, Q = UIsinφ = -UI, следовательно на C – элементе происходит обмен энергией между источником электрической энергии и электрическим полем конденсатора, что определяет реактивную мощность Q.
c = Р ± jQ , угол сдвига фаз φ = -90о, тогда Р = UIcosφ = 0, Q = UIsinφ = -UI, следовательно на C – элементе происходит обмен энергией между источником электрической энергии и электрическим полем конденсатора, что определяет реактивную мощность Q.
С - элемент работы не совершает, поэтому активная мощность равна 0.
 c= - jQ.
c= - jQ.
Электрическая цепь с индуктивным L - элементом
Идеальная катушка индуктивности имеет активное сопротивление RL=0.
|
| i(t) = Imsin(ωt + ψi) eL = - L eL = Emsin(ωt + ψi + 90°) u = - eL; u(t) = Um sin(ωt + ψu) |
начальная фаза ψu = ψi + 90°
угол сдвига фаз φ = ψu - ψi = 90о
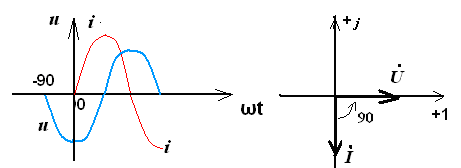
Из векторной диаграммы видно, что ток на катушке индуктивности напряжение опережает ток на 900, так как φ = 900, то Z = Zcos(90о) + jZsin(90о) = jZ, а модуль комплексного сопротивления Z = XL = ωL, следовательно сопротивление чисто реактивное и равно:
ZL = jZ = Z
Закон Ома: U = I·(XL)
Мощность на L - элементе: S = Р ± jQ , угол сдвига фаз φ = 90о, тогда
Р = UIcosφ = 0, Q = UIsinφ = UI, следовательно на L – элементе происходит обмен энергией между источником электрической энергии и магнитным полем катушки, что определяет реактивную мощность Q. L - элемент работы не совершает, поэтому активная мощность равна 0.
 L = jQ
L = jQ
Реальная катушка имеет активное сопротивление, определяемое сопротивлением проводов, поэтому полное комплексное сопротивление равно:
ZL= RL + jXL
Анализ цепей синусоидального тока
1. Анализ цепей синусоидального тока происходит при условии, что все элементы цепи идеальны, т.е. R, L, C идеальны.
Электрическое состояние цепей синусоидального тока описывается теми же законами, что и в цепях постоянного тока.
Закон Ома: 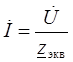
Первый закон Кирхгофа в тригонометрическом виде: 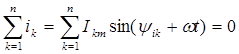
Первый закон Кирхгофа в комплексном виде: 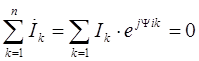
Второй закон Кирхгофа в тригонометрическом виде: 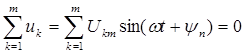
Второй закон Кирхгофа в комплексном виде: 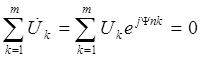
Алгебраическая сумма комплексных напряжений на пассивных элементах равна сумме сторонних ЭДС входящих в этот контур. m – число участков контура Правила знаков при составлении уравнений такие же что в цепях постоянного тока.
Последовательное соединение элементов в цепи синусоидального тока:
цепь RLC
|
| По второму закону Кирхгофа в комплексной форме
|
Zэкв – модуль эквивалентного сопротивления (полное сопротивление определяет связь между U и I)
 - аргумент, связь между начальными фазами
- аргумент, связь между начальными фазами 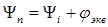
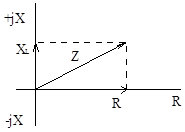
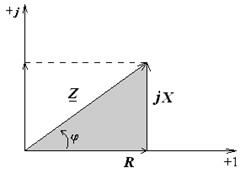
Треугольники сопротивлений и напряжений
|
|
X – реактивное сопротивление X = XL - XC
X – алгебраическая величина, его знак зависит от соотношения XL и XC |
Из треугольника:



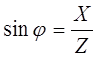
 ;
; 
 комплексное сопротивление
комплексное сопротивление
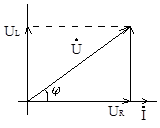
Треугольник напряжений
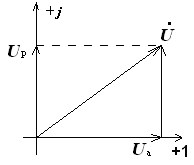
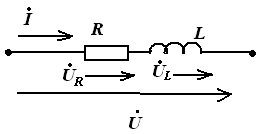
Цепь RL
|
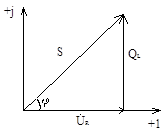
Мощности в RL цепи
|
Треугольник напряжений
Треугольник сопротивлений
Треугольник мощностей |
RC-цепь
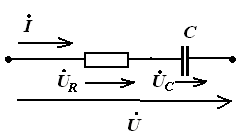
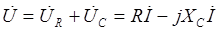


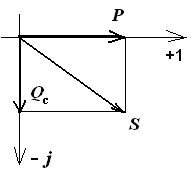
Вместе с этой лекцией читают "3.Просветительский характер героического в романтических героях Стендаля.".
Треугольник сопротивлений треугольник напряжений Треугольник мощностей


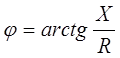
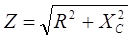
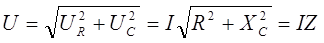
Если цепь состоит из последовательно соединенных элементов с активным и реактивным сопротивлением, то векторная диаграмма имеет вид прямоугольного треугольника.



 ; Z = R
; Z = R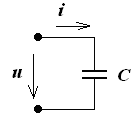
 = C
= C = C·ω·Umcos(ωt+ ψu)
= C·ω·Umcos(ωt+ ψu)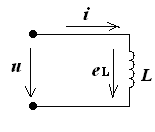
 = - LωImcos(ωt + ψi)
= - LωImcos(ωt + ψi)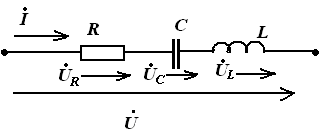

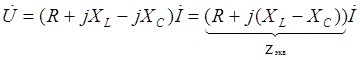
 - закон Ома
- закон Ома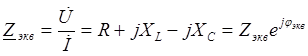
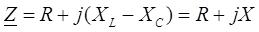
 ;
;  ;
; 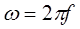
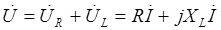
 ;
;