Косой изгиб. Общие понятия о косом изгибе
7 Сложное сопротивление
Рассмотренные нами до сих пор случаи нагружения элементов конструкций (растяжение-сжатие, сдвиг, кручение, плоский изгиб) относят сопротивление стержня к одному (простому) виду деформации. Сложным соответствует два и более простых видов.
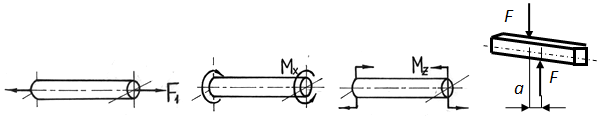
Рис.43. Простое сопротивление.
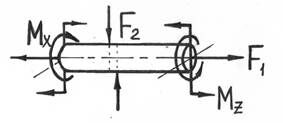
Рис. 44. Сложное сопротивление
Сложное сопротивление – вид нагружения, представляющий собой комбинацию (сочетание) нескольких простых видов сопротивления.
В случае сложного сопротив-ления в поперечных сечениях элемента возникает два и более внутренних силовых факторов. При этом расчет элементов при сложном сопротивлении ведется на основании принципа независимости действия сил. То есть, каждый из простых видов сопротивления, входящих в состав сложного, рассматривается независимо от остальных, а затем находится суперпозиция (сумма) полученных решений (для внутренних усилий, напряжений, деформаций и т.д.). Принцип суперпозиции применим только для линейно-упругих систем.
7.1 Косой изгиб. Общие понятия о косом изгибе
Рекомендуемые материалы
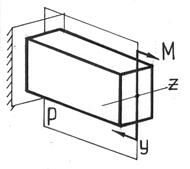
Рис.45. Плоский изгиб
Прежде чем перейти к рассмотрению некоторых характерных для инженерной практики случаев сложного сопротивления и, в частности, косого изгиба, вспомним, что до этого мы анализировали частный случай изгиба, который называли плоским, – когда плоскость действия сил совпадала с одной из главных плоскостей инерции балки. Однако существуют и более общие случаи изгиба, когда силы действуют в плоскости, не совпадающей с плоскостью инерции (косой изгиб), или, вообще, силы не лежат в одной плоскости (сложный или неплоский изгиб).
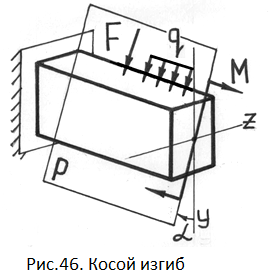
Косой изгиб – изгиб, при котором плоскость P действия изгибающих моментов и поперечных сил не совпадает ни с одной из главных плоскостей инерции бруса.
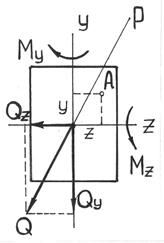
Рис.47. Внутренние усилия в балке при косом изгибе
Определение внутренних усилий при косом изгибе. При косом изгибе в поперечных сечениях бруса действуют следующие внутренние усилия: Mz, My – изгибающие моменты и Qy, Qz –поперечные (перерезывающие) силы. Это легко показать мысленно рассекая стержень и определяя внутренние усилия при косом изгибе консольной балки под действием сосредоточенной силы F на свободном конце (см. рис.47):
Информация в лекции "Типы зарубежных туристических регионов" поможет Вам.
(7.1)
Правило знаков для внутренних усилий: изгибающие моменты – положительны, если вызывают растяжение в положительном квадранте координатной системы zOy; поперечные силы – положительны, если под их действием отсеченный элемент поворачивается по часовой стрелке.
Таким образом, косой изгиб может быть представлен как совместное действие двух плоских изгибов в двух взаимно перпендикулярных плоскостях инерции.
Для определения полного изгибающего момента M и полной поперечной силы Q при косом изгибе достаточно определить внутренние усилия для каждого из плоских изгибов в отдельности (то есть Qy, Mz и Qz, My), а затем найти их векторную сумму:
. (7.2)
