Предел последовательности. Предел функции

Предел последовательности. Предел функции

            В этом параграфе мы обобщим понятие предела числовой последовательности и сформулируем понятие предела последовательности точек евклидова пространства , а затем дадим понятие предела векторной функции векторного аргумента, т.е. функции вида (1) из введения к главе 2.

            Договоримся впредь называть координатами точки   координаты вектора  в выбранном базисе.

            Определение 2.9. Точка  называется пределом последовательности  точек пространства , если для любого положительного  существует такое натуральное число (зависящее от ), что для всякого  .

            Как и для предела числовой последовательности будем в этом случае писать:

           

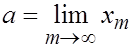
            Чтобы подчеркнуть зависимость указанного  от , пишут .

            Таким образом, понятие предела векторной последовательности по существу ничем не отличается от понятия предела числовой последовательности, но вместо модуля разности  (расстояния между точками числовой прямой) фигурирует расстояние между точками (векторами) пространства .

            С каждой последовательностью  векторов  ассоциируется  числовых последовательностей  , которые мы назовем координатными последовательностями исходной векторной последовательности - по определению это последовательности координат точек (векторов) исходной последовательности.

Рекомендуемые материалы

            Положим  - - ая координата точки . Следующая теорема сводит понятие и вычисление предела векторной последовательности к понятию и вычислению предела обычной числовой последовательности.

            Теорема 2.2 . Точка есть предел последовательности  тогда и только тогда, когда для каждог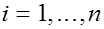о  число  есть предел - ой координатной последовательности, т.е.

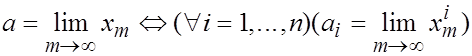
            Доказательство. Пусть 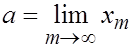. Тогда для любого  найдется натуральное  такое, что как только , так .

            Но .

            Следовательно,

,

и  для каждого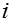

            .

            Обратно, пусть для каждого .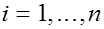

            Тогда для любого  найдутся такие натуральные , что как только , так , 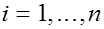. Выбирая , получим, что для любого  одновременно будут выполнены неравенства  для всех .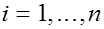

            Значит,

.

            Так как  - фиксированное число (размерность пространства), то отсюда вытекает, что

            .

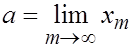            Теорема доказана.

            Совершенно аналогично скалярному случаю строится и понятие предела функции.

            Определение 2.10. Точка  называется пределом функции  при  (или пределом в точке ), если для любого  существует такое (зависящее от ), что как только  так .

            Обозначение: .

            Опять-таки, желая подчеркнуть зависимость  от , будем писать .

            Несмотря на то, что в векторном случае понятие предела функции внешне ничем не отличается от такового в «одномерном анализе», здесь возникают более сложные и тонкие ситуации при вычислении пределов и при рассмотрении вопроса об их существовании.

            Все хорошо помнят из одномерного анализа первого семестра понятие одностороннего предела функции в точке. Образно рассуждая, аргумент может приближаться к некоторой точке как слева, так и справа, в зависимости от чего предел функции в данной точке может меняться (левый и правый пределы в точке соответственно). В векторном случае «способов приближения» к точке у аргумента неизмеримо больше, и мы должны формализовать возникающую тут более общую и более сложную ситуацию зависимости предела от «траектории приближения» аргумента к заданной точке.

            С этой целью введем понятие предела по множеству.

            Определение 2.11. Точка  называется пределом функции  по множеству  при  (или пределом в точке по множеству ), если для любого  существует такое , что как только  и  так .

            Обозначение: .

            Таким образом, в определении 2.11, в существенном отличии от определения 2.10, накладывается ограничение на «траекторию приближения» аргумента к заданной точке: аргумент должен не только попасть в -окрестность точки , но, попав туда, оказаться еще и в заданном множестве  (см. рис.2. 7).

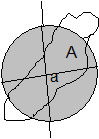
Рис. 2.7

            Нетрудно понять, что предел функции в точке существует тогда и только тогда, когда в этой точке существует предел данной функции по любому множеству (или, что равносильно, предел в точке не зависит от «траектории приближения» аргумента к этой точке).

            Другая трактовка предела функции в точке состоит в понимании его как предела по множеству, совпадающему со всем пространством.

            Рассмотрим некоторые примеры.

1)  Зададим функцию  следующим образом:

           

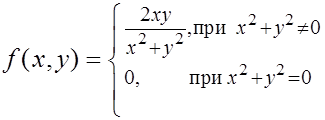
            Выясним, существует ли предел этой функции в точке .

            Имеем:

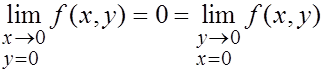
Это значит, что в заданной точке функция имеет предел, равный нулю, по множествам: 1) точек оси абсцисс () и 2) точек оси ординат (). Другим словами, при приближении к началу координат вдоль каждой из осей предел существует и равен нулю.

            Но рассмотрим теперь предел по множеству точек какой-нибудь прямой , где .

            Имеем:

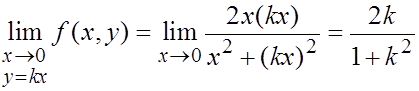
            Полученный результат показывает, что значение предела функции в рассматриваемой точке зависит от выбираемого множества: по разным лучам, пересекающимся в начале координат, мы имеем разные значения предела. Следовательно, предел данной функции в данной точке не существует.

2)  Функция определена формулой:

           

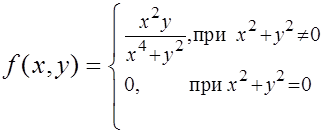
            Полагая  (для любого конечного , отличного от нуля), получим:

            Нетрудно показать (упражнение!), что и по каждой из осей (т.е. при ) предел будет равен нулю.

            Таким образом, при приближении к началу координат по любой прямой предел существует и равен нулю.

            Но пусть теперь . Тогда:

Бесплатная лекция: "МАСЛОУ Абрахам Хоралд" также доступна.

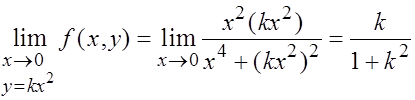
            Это значит, что при приближении к заданной точке по параболе предел функции в точке зависит от параметра параболы. Тогда и предел функции в данной точке не существует.

            Общий вывод таков: существование предела функции в точке по некоторому множеству (и даже по различным множествам) не гарантирует существование предела в точке. Это совершенно аналогично тому, что в одномерном анализе существование односторонних пределов не означает существование предела.

            Замечание. Иногда определение предела функции в точке дается через проколотую окрестность точки, т.е. принимается, что

           

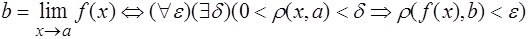
            Если используется такое определение предела, то предел функции в точке может существовать, когда значение функции в точке определено, но не равно значению предела функции в этой точке. Если же рассматривается определение 2.10, то такая ситуация не может иметь места. А именно, предел функции в точке в смысле определения 2.10 может существовать, если значение функции в точке не определено, или значение функции в точке определено и равно значению предела (непрерывность). Заметим, что написанное выше определение предела (через проколотую окрестность) можно рассматривать как определение предела по множеству .