Вычислительная сложность алгоритмов
Вычислительная сложность алгоритмов
Методы решения многих задач математики носят алгоритмический характер. Для задач, имеющих практический интерес, ищут именно разрешающие алгоритмы. Уточнение понятия алгоритма позволило выявить алгоритмически неразрешимые проблемы.
Исследуя задачи на дискретных конечных математических структурах, как правило, можно найти комбинаторные алгоритмы для их решения, например, с помощью некоторого процесса перебора. Однако при этом число шагов быстро растет с увеличением размерности задачи, и последняя становится практически неразрешимой.
Поиск эффективных алгоритмов для решения задач дискретной математики привел к одной из важнейших ее проблем - к решению вопроса о возможности исключения перебора вариантов в комбинаторных алгоритмах.
В самом широком смысле эффективность алгоритма связана со всеми вычислительными ресурсами, необходимыми для его работы. Однако обычно под наиболее эффективным понимается наиболее «быстрый» алгоритм.
Есть целый ряд задач, представляющих практический интерес, для которых не существует эффективных алгоритмов, а про имеющиеся разрешающие алгоритмы можно сказать, что они неэффективны даже при реализации на ЭВМ будущих поколений.
Оценка сложности алгоритмов и создание эффективных алгоритмов - одна из важнейших задач современной дискретной математики.
Существует много критериев оценки алгоритмов. Но можно сказать, что одним из самых важных критериев является его временная сложность. Время работы алгоритма можно выразить в виде функции от «размеров» входных данных, требуемых для описания задачи. Входные и выходные данные можно кодировать некоторым «разумным» способом в виде двоичных последовательностей из нулей и единиц. Тогда алгоритм можно рассматривать как последовательность двоичных операций, работающих с памятью из двоичных же символов.
Временная сложность алгоритма отражает затраты времени (число шагов), требуемые для его работы. Это функция, которая каждой входной длине n ставит в соответствие минимальное время, затрачиваемое алгоритмом на решение всех однотипных индивидуальных задач этой длины.
Рекомендуемые материалы
Из курса математического анализа известно, что функция f(n) есть O(g(n)), если существует константа c, такая что |f(n)| <= c(g(n)) для всех n >= 0.
Полиномиальным алгоритмом (или алгоритмом полиномиальной временной сложности) называется алгоритм, у которого временная сложность равна О(Р(n)), где Р(n) — некоторая полиномиальная функция от входной длины n. Алгоритмы, для временной сложности которых не существует такой оценки, называются экспоненциальными.
Задача считается труднорешаемой, если для нее не существует разрешающего полиномиального алгоритма.
Кажется, что по мере совершенствования вычислительной техники и роста ее быстродействия проблема оптимизации алгоритмов не должна стоять так остро. Но следующие табл. 2, 3 демонстрируют обратное. Из последней таблицы видно, что повышение быстродействия машины не дает существенного роста размерности разрешимых задач, если алгоритм имеет экспоненциальную сложность.
Таблица 2
Оценка зависимости времени работы алгоритмов сложности, равной n, n3, 2n, от размеров входной информации
| Функция временной сложности | Размерность n | |||
| 10 | 20 | 50 | 60 | |
| n | 0,00001 секунд | 0,00002 секунд | 0,0005 секунд | 0,0006 секунд |
| n3 | 0,001 секунд | 0,008 секунд | 0,125 секунд | 0,216 секунд |
| 2n | 0.001 секунд | 1,0 секунд | 35,7 дней | 366 столетий |
Таблица 3
Оценка максимальной размерности задачи, решаемой за один час
| Функция временной сложности | Современная ЭВМ | ЭВМ, в 100 раз более быстрая | ЭВМ, в 1000 раз более быстрая |
| n | N1 | 100 N1 | 1000 N1 |
| n3 | N2 | 4.64 N2 | 10 N2 |
| 2n | N3 | N3 + 6.64 | N3 + 9.97 |
Многие прикладные задачи могут быть сформулированы в терминах теории графов. Однако при решении реальных задач характеристики соответствующих графов (например, число вершин n и число ребер m) весьма велики, и их анализ возможен лишь с привлечением ЭВМ.
Задача поиска эффективных алгоритмов в теории графов имеет большое практическое значение. Поэтому в заключение дадим краткий обзор временной сложности рассмотренных нами комбинаторных алгоритмов на графах.
Задачи теории графов можно классифицировать следующим образом:
1) задачи, для которых имеются алгоритмы сложности O(n + m);
2) задачи, для которых известны алгоритмы сложности О (Р(n + m)), где Р — нелинейный полином;
3) задачи, для которых известны только алгоритмы экспоненциальной сложности, но про которые нельзя сказать, что для них нет алгоритмов полиномиальной сложности;
4) задачи, которые могут быть решены лишь с использованием алгоритма экспоненциальной сложности.
Информация в лекции "1. Основные определения" поможет Вам.
Разбиение задач на первые три класса зависит от мастерства математика. Однако задачи четвертого класса принципиально нельзя отнести к первым трем классам, поскольку они включают в себя экспоненциальные процедуры, например, просмотр всех подграфов исходного графа.
К четвертому классу относятся задачи перечисления всех остовных деревьев графа и перечисления всех циклов графа. Это объясняется тем, что у полного n-вершинного графа число остовных деревьев равно nn-2 , число циклов длины i равно Cin(i - 1)!, т. е. общее число циклов составляет
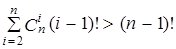 |
К первому классу относятся, например, следующие задачи: поиск остовного дерева графа; выделение компоненты связности графа и сильной связности орграфа; нахождение минимального пути в орграфе (или минимального маршрута в графе). Для решения этих задач построены алгоритмы, имеющие сложность О(n + m).
Второй класс в настоящее время включает в себя такие задачи: нахождение матрицы связности; нахождение минимального пути в нагруженном графе (сложность алгоритма О(n3)); нахождение минимального остовного дерева в нагруженном графе (сложность алгоритма О (n2)).
Третий класс содержит следующие задачи: о существовании в графе гамильтонова цикла (задача коммивояжера); об определении изоморфизма данного графа G1 какому-нибудь подграфу графа G2, и многие другие задачи. Для решения этих задач не существует полиномиальных алгоритмов, хотя не кажется безусловным, что их решение возможно лишь с помощью экспоненциальных алгоритмов. Для многих задач этого класса справедливо следующее свойство сводимости: существование полиномиального алгоритма для решения одной из них дало бы полиномиальный алгоритм для решения другой. В современной дискретной математике третий класс задач является предметом пристального изучения.






















