Доказать теорему Ролля
Доказать теорему Ролля.
Пусть дана функция  .
.
1. Определена и непрерывна на отрезке  .
.
2. Дифференцируема на интервале 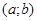 .
.
3. И на концах отрезка принимает одинаковые значения.  .
.
Тогда найдется, по крайней мере, 1 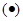
 , принадлежащая интервалу
, принадлежащая интервалу  .
.
Доказательство: Т.к. функция  непрерывна на отрезке
непрерывна на отрезке  , то согласно 2 теореме Вейерштрасса она достигает своего минимального и максимального значения.
, то согласно 2 теореме Вейерштрасса она достигает своего минимального и максимального значения.
Вам также может быть полезна лекция "4.1 Образование Поместного приказа".
 ,
,  ,
,
 ,
,  .
.
Случаи:
1.  ,
,  - любое из интервала
- любое из интервала 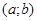
2.  в силу 3-го условия теоремы, одно из значений минимального или максимального достигается функцией во внутренней точке интервала
в силу 3-го условия теоремы, одно из значений минимального или максимального достигается функцией во внутренней точке интервала 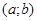 .
.
Согласно второму условию теоремы Ролля, функция дифференцируема на интервале 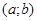 в любой точке, то по теореме Ферма существует
в любой точке, то по теореме Ферма существует  .
.






















