Доказать теорему Бернулли-Лопиталя для предела отношения двух бесконечно малых функций

Доказать теорему Бернулли-Лопиталя для предела отношения двух бесконечно малых функций.

Теорема. Пусть ф-ции f(x) и g(x) определены и дифференцируемы в , представляют собой б.м.ф. при , причем  в . Если .

Доказательство: Рассмотрим {. Доопределим по непрерывности данные функции нулем в точке a (f(a)=0, g(a)=0). Тогда на [a, ] функции f(x) и g(x) непрерывны, на (a; ) f(x) и g(x) дифференцируемы. По теореме Коши   при  по условию теоремы >

Замечание 1: точка а может быть бесконечной, тогда  или  Формулировка: пусть f(x) b g(x)  определены и дифференцируемы на   и представл. Б.м.ф. при , причем  Если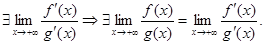

Замечание 2: если  и  удовлетворяют всем условиям Б-Л и , то  и т. д.