Определение границ слоев по количественной переменной
7. Определение границ слоев по количественной переменной
Пусть H - фиксированное число слоев.
Определим слои следующим образом:
Uh = { k ÎU, xh-1 £ xk £ xh,} h = 1...H, при x0 = -¥ , а xH = + ¥ .
Какими выбрать границы слоев  ?
?
Предположим, что
§ совокупность достаточно большого объема;
§ базовая и целевая переменные совпадают: x = y
Эмпирическое распределение признака y аппроксимируем с помощью непрерывной плотности f(x).
Рекомендуемые материалы
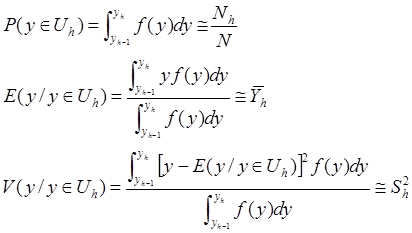
1) Случай пропорционального размещения.
Нужно минимизировать:
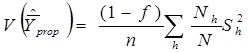
Не учитывая констант n, N и пренебрегая разницей между  и
и  перепишем дисперсию оценки в виде:
перепишем дисперсию оценки в виде:
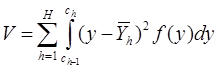
Нужно найти значения  , минимизирующие V
, минимизирующие V
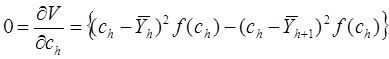
Если  то решением будет:
то решением будет:
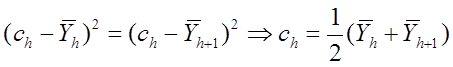 |
Следовательно, точки разбиения нужно выбирать так, чтобы они были равны полусумме средних значений тех двух слоев, границей которых они являются.
2) Случай оптимального размещения.
Нужно минимизировать:
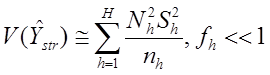
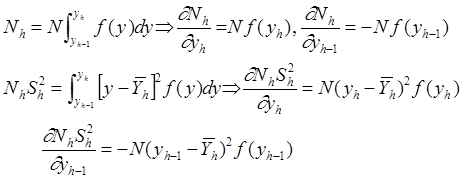
Из  выводим:
выводим:
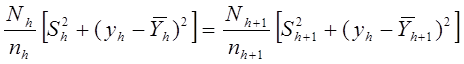
Проблема: минимизация дисперсии должна проводится одновременно по  :
:
Вам также может быть полезна лекция "15 Способы получения и использования доказательств".
® заменяем  на
на  , (оптимальность по
, (оптимальность по  )
)
откуда:
 (1)
(1)
В формулу входят не только средние, но и дисперсии слоев. Поэтому на практике используются приближения для (1).
Например, приближение, полученное Экманом (1959):
Границы слоев формировать таким образом, чтобы
 , где
, где  - границы.
- границы.




















