Оптимальное размещение
6. Оптимальное размещение
6.1. Оптимальное размещение при фиксированном объеме выборки
Цель – найти значения 
,...,
,...,
, которые минимизируют дисперсию оценки суммы:
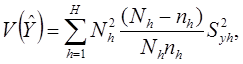
при условии, что
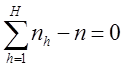
Это задача нахождения условного экстремума.
Функция Лагранжа имеет вид:
Рекомендуемые материалы
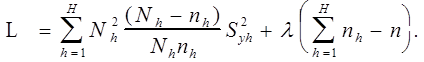
Приравниваем нулю частные производные по :
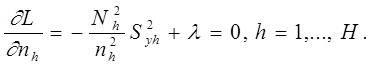
Получаем
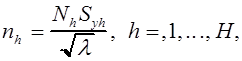
в силу условия, что 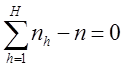имеем
Следовательно
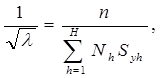
что дает
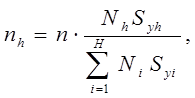
Замечание.
Проверить, что это действительно минимум можно рассчитав вторые частные производные по .
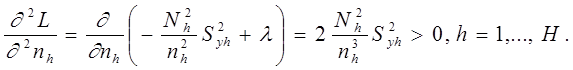
Вывод.
Следует больше представлять в выборке те слои, в которых среднее квадратическое отклонение признака больше.
Проблема.
Дисперсии признака в слоях должны быть известными.
Пример 5.
В условиях примера 4 определим оптимальное размещение выборки по слоям и спрогнозируем соответствующую точность оценки среднего. Имеем
| Интервалы группировки |
|
|
|
|
| 0-9 | 500 | 1.5 | 612,4 | |
| 10-19 | 300 | 4 | 600,0 | |
| 20-49 | 150 | 8 | 424,3 | |
| 50-499 | 100 | 100 | 1000,0 | |
| 500 и более | 10 | 2500 | 500,0 | |
| Всего | 1060 | 7803,7 | 3136,6 |
?Так как
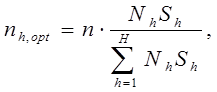
вычисляем
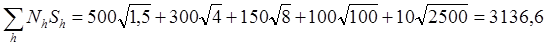
Применяем формулу оптимального размещения с 
:
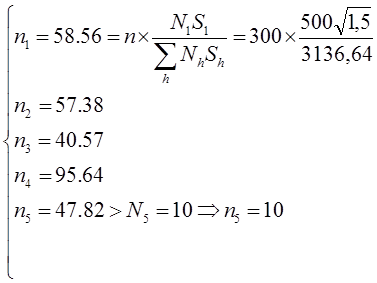
Включаем слой 5 целиком в выборку и повторяем расчеты с 
:
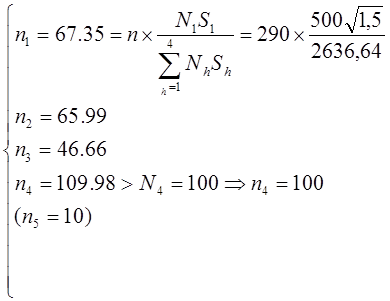
Включаем слой 4 также целиком в выборку и повторяем расчеты с 
:
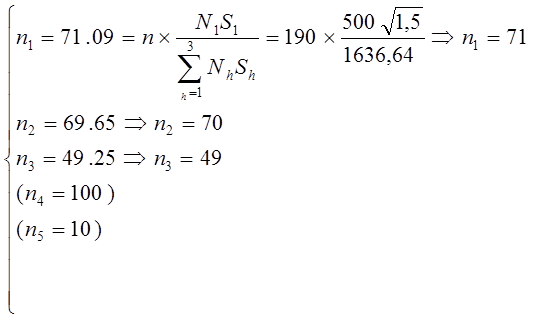
В случае оптимального размещения общая формула дисперсии оценки среднего имеет вид:
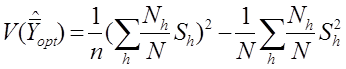
Проведя вычисления, получаем
| Интервалы группировки |
| Дисперсия оценки среднего | Коэффициент вариации оценки |
| 0-9 | 71 | 0,01813 | 0,02693 |
| 10-19 | 70 | 0,04381 | 0,01744 |
| 20-49 | 49 | 0,10993 | 0,01105 |
| 50-499 | 100 | 0 | 0,00000 |
| 500 и более | 10 | 0 | 0,00000 |
| Всего | 300 | 0,00974 | 0,00331 |
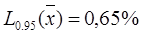
Эффект плана соответственно составляет:
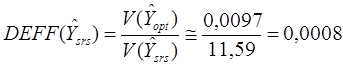
6.2. Оптимальное размещение при фиксированных общих затратах
Предположим, что затраты на обследование можно записать в следующем виде:
,
где 
- затраты на наблюдение единицы в h-ом слое.
Две «противоположные» задачи:
1. Определить значения , минимизирующие дисперсию 
при заданной величине общих затрат (C).
2. Определить значения , минимизирующие затраты (C) при заданном уровне точности .
Теорема 3.
Значения , минимизирующие дисперсию при заданных общих затратах (C), определяются по формуле
,
при этом минимальная дисперсия равна
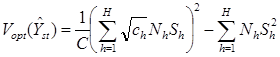
Доказательство.
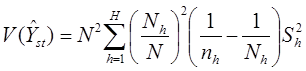
Лагранжиан равен: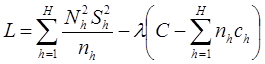 
,
и 
определяется из условия: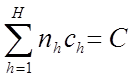 
Теорема 4.
Значения , минимизирующие полные затраты (C) при заданной точности , определяются по формуле
,
Минимальные затраты равны
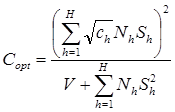
Доказательство.
Лагранжиан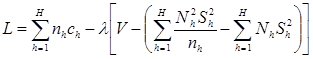 
,
и определяется из условия 
.
При оптимальных значениях : 
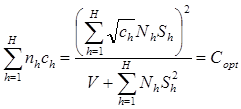
Интерпретация
В обоих случаях:
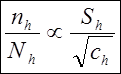
Поэтому в выборке наиболее представлены те слои, в которых:
· дисперсия признака больше;
· затраты на обследование самые низкие.
Замечания.
· Значения должны быть целочисленными.
· Если при определении размещения в некоторых слоях полученные 
, то
* принимаем 
для этих слоев,
* пересчитываем значения для других слоев, соответствующие оптимальному распределению:
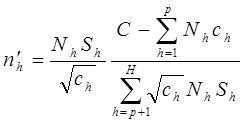
* выполняем итерации, пока имеются слои, для которых nh > N h.
· Можно задать дополнительные условия:
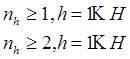
6.3 Практическое использование
Рассмотрим оптимальное размещение Неймана
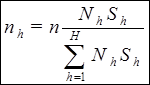
Ясно, что дисперсии 
должны быть заранее известны.
Возможно несколько решений:
· использовать оценки дисперсий , полученные из предшествующего обследования;
· экспертные оценки или тестовое исследование;
· использование вспомогательной переменной (x) сильно коррелированной с переменной (y), значения которой известны для всех единиц совокупности:
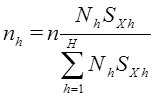
· Если верна гипотеза о равенстве коэффициентов вариации в слоях, то так как
, тогда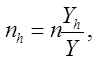 
· Степенное размещение: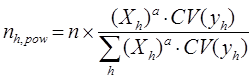 
Замечание.
Степенное размещение обеспечивает приблизительно одинаковые по точности результаты в слоях. Показатель степени (
) обычно выбирается равным 1, 1/2, или 1/3.
6.4 Эффективная стратификация для нескольких переменных
Оптимальное размещение для переменной (y) может дать для других переменных существенно меньшую точность, чем та, которая может быть получена при простой случайной выборке.
Рекомендация:
Ещё посмотрите лекцию "7 Память. Микросхемы SDRAM" по этой теме.
§ Можно использовать пропорциональное распределение, что часто оказывается хорошим компромиссом.
§ Другим решением является взвешивание основных переменных на основе их дисперсии:
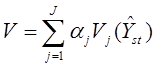
с дальнейшей минимизацией дисперсии (V) при фиксированных затратах (C) или же наоборот:
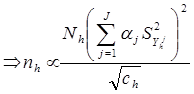
Задача состоит в правильном выборе значений 
.
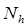
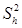
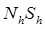
