Десятичные дроби и действительные числа
§ 2. Десятичные дроби и действительные числа
Дроби, у которых знаменатель представляет собой степень десятки, т.е. 10, 102 = 100, 103 = 1000 и т.д., называются десятичными дробями. Записываются они особым образом:
 ; 1
; 1 ; 2
; 2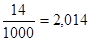
Попытка записать любую обыкновенную дробь в виде десятичной дроби приводит иногда к бесконечной десятичной дроби. Например, разделив «уголком», мы получим: •
 =0,333...;
=0,333...;  =0,90909...;
=0,90909...;
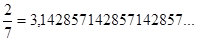
Как видно, получающаяся бесконечная последовательность цифр содержит так называемый период — один и тот же повторяющийся набор цифр. Поэтому полученные десятичные дроби называют бесконечными периодическими десятичными дробями. Можно доказать, что любая обыкновенная дробь записывается в виде бесконечной периодической десятичной дроби. Обратное также верно: любая бесконечная периодическая десятичная дробь представляет собой десятичную запись некоторой обыкновенной дроби. Как найти последнюю, поясним на примере.
Пример. Превратим в обыкновенные дроби числа q = 0,777... и р = 0,999...
Умножив на 10, получаем:
Рекомендуемые материалы
1) 10q = 7,777... = 7 + q, откуда 9q = 7 и q = .
.
Проверьте результат, превратив 7/9 в десятичную дробь.
2)10р = 9,999... = 9 + р, откуда 9р = 9 и р = 1. Заметим, что 1 можно записать в виде бесконечной десятичной дроби с периодом 0: 1,000...; аналогично, 0,24 = = 0,24000..., 3,5 = 3,5000... и т.п.
УПРАЖНЕНИЯ
8. С помощью калькулятора и «вручную» превратите данную обыкновенную дробь в бесконечную периодическую десятичную дробь и укажите период:  ,
,  ,
,  ,
,  .
.  .
.
9. Превратите бесконечную периодическую десятичную дробь в обыкновенную: 1,888...; 0,1212...; 0,444...
Решив эти примеры, каждый будущий юрист задаст себе вопрос: а имеют ли смысл бесконечные непериодические десятичные дроби?
Рассмотрим равнобедренный прямоугольный треугольник, длина катетов которого равна единице. Обозначим длину гипотенузы через х. По теореме Пифагора
X2=12 + 12 = 2. (1)
Докажем, что корни этого уравнения не являются рациональными числами. В самом деле, предположим противное, т.е. что корнем уравнения (1) является дробь х =  (a и b — целые числа). Если дробь
(a и b — целые числа). Если дробь  можно сократить, сделаем это, и будем полагать далее, что дробь
можно сократить, сделаем это, и будем полагать далее, что дробь  является уже несократимой.
является уже несократимой.
Подставляя  в уравнение (1), получим
в уравнение (1), получим  = 2 или
= 2 или
a2 = 2b2 (2)
Так как в правую часть равенства (2) входит множитель 2, то а2 — число четное. Следовательно, число а также четное и его можно записать в виде а = 2с. Подставив в (2), получим (2с)2 = 2b2 или, сократив на 2, 2с2 = b2. Отсюда следует, что число b2 также является четным. Но тогда четным будет и число b. Теперь, поскольку оба числа а и bполучились четными, дробь  является сократимой. Это противоречит сделанному выше предположению, что дробь
является сократимой. Это противоречит сделанному выше предположению, что дробь  — несократимая. Противоречие возникло вследствие того, что в самом начале было сделано неверное предположение — корнем уравнения (1) является рациональное число — дробь
— несократимая. Противоречие возникло вследствие того, что в самом начале было сделано неверное предположение — корнем уравнения (1) является рациональное число — дробь  . Следовательно, никакая дробь не может быть корнем уравнения (1), что и требовалось доказать.
. Следовательно, никакая дробь не может быть корнем уравнения (1), что и требовалось доказать.
Результат наших рассуждений можно сформулировать иначе: квадратный корень из числа 2 не является рациональным числом, т.е. бесконечной периодической десятичной дробью.
Будем искать приближенные значения числа х =  . Ясно, что 1 < х < 2. Далее, так как 1,42 = 1,96 < 2 = х2, а 1,52 = 2,25 > 2 = х2, то 1,4 < х < 1,5. Это означает, что с точностью до 0,1 число х приближенно равно 1,4, (я » 1,4). Аналогично устанавливаем, что 1,41 < х < 1,42, так как 1,412 < 2, а 1,422 > 2. Следовательно, с точностью до 0,01 получаем х » 1,41. Применив еще раз тот же прием, найдем, что 1,414 < х < 1,415, т.е. х » 1,414, и т.д.
. Ясно, что 1 < х < 2. Далее, так как 1,42 = 1,96 < 2 = х2, а 1,52 = 2,25 > 2 = х2, то 1,4 < х < 1,5. Это означает, что с точностью до 0,1 число х приближенно равно 1,4, (я » 1,4). Аналогично устанавливаем, что 1,41 < х < 1,42, так как 1,412 < 2, а 1,422 > 2. Следовательно, с точностью до 0,01 получаем х » 1,41. Применив еще раз тот же прием, найдем, что 1,414 < х < 1,415, т.е. х » 1,414, и т.д.
Описанная процедура позволяет находить все более точные приближения числа  . Но ни одно из этих приближений не может быть равным
. Но ни одно из этих приближений не может быть равным  , так как все приближенные значения являются рациональными числами, а мы доказали, что
, так как все приближенные значения являются рациональными числами, а мы доказали, что  не является рациональным числом. Поэтому последовательность приближенных значений будет бесконечной.
не является рациональным числом. Поэтому последовательность приближенных значений будет бесконечной.
Итак, число  представляется в виде бесконечной последовательности приближенных значений. Каждое последующее значение получается добавлением к предыдущему нового десятичного знака. Это позволяет записать
представляется в виде бесконечной последовательности приближенных значений. Каждое последующее значение получается добавлением к предыдущему нового десятичного знака. Это позволяет записать  в виде бесконечной десятичной дроби:
в виде бесконечной десятичной дроби:
 =1,414213662373...
=1,414213662373...
Описанным способом можно находить десятичные приближения любого числа. Для обыкновенных дробей — это просто деление уголком (cм. выше), которое приводит к бесконечным периодическим дробям. Поскольку число  не является рациональным, то представляющая его бесконечная десятичная дробь не будет периодической. Таким образом мы приходим к понятию бесконечной непериодической десятичной дроби.
не является рациональным, то представляющая его бесконечная десятичная дробь не будет периодической. Таким образом мы приходим к понятию бесконечной непериодической десятичной дроби.
Для чисел вида  , а Î N также имеются процедуры, позволяющие найти любое число знаков в их десятичной записи. Один из таких алгоритмов мы приводим ниже без описания: Это ребус посложнее, чем деление «уголком». Попробуйте его разгадать.
, а Î N также имеются процедуры, позволяющие найти любое число знаков в их десятичной записи. Один из таких алгоритмов мы приводим ниже без описания: Это ребус посложнее, чем деление «уголком». Попробуйте его разгадать.
 =1,414...
=1,414...  =2,236...
=2,236...
| 1 | ||||
| 24 ´4 | 100 – 96 | 42 ´ 2 | 100 –84 | |
| 281 ´1 | 400 –281 | 443 ´ 3 | 1600 –1359 | |
| 2824 ´ 3 | 11900 –11296 | 4466 ´ 6 | 27100 –26796 | |
| ... | ... | ... | ... |
Найдите еще несколько знаков и проверьте результат с помощью калькулятора.
Заметим, что всякую бесконечную десятичную дробь можно записать в виде суммы бесконечного числа слагаемых:
 = 0,333... =
= 0,333... =  +
+  +
+  + ...;
+ ...;
 = 1 +
= 1 + +
+  +
+  + ...
+ ...
Такие суммы называются рядами. Первый ряд представляет собой так называемую бесконечную геометрическую прогрессию, с которой, возможно, Вы познакомились в школе. Второй ряд прогрессией уже не является. В школе Вы решали квадратные, кубические и биквадратные уравнения. Их корни выражаются через радикалы второй, третьей или четвертой степени. Например, уравнение х3 = 5 имеет корень х = , уравнение 2х2 = 3 — корни х =
, уравнение 2х2 = 3 — корни х =  и х = –
и х = – . Корни квадратного уравнения
. Корни квадратного уравнения
ах2 + bх + с = 0
вычисляются по формуле
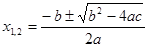
В школьных учебниках числа а, b и с обычно подбирают так, чтобы под корнем получался квадрат целого числа. Но, если коэффициенты уравнения не подбирать специально, то корни х1 и х2 будут, вообще говоря, бесконечными непериодическими десятичными дробями. Наиболее общий результат формулируется так: корень любого алгебраического уравнения
а0хп + a1xn–1 + а2хп -2 + ... + ап-1 + ап = 0 (3)
степени п с целыми коэффициентами (если этот корень существует!) является, вообще говоря, бесконечной непериодической десятичной дробью.
Помимо алгебраических уравнений, существуют другие источники получения бесконечных непериодических десятичных дробей.
Определим два очень важных числа. Первое из них — число p, равное отношению длины I произвольной окружности к ее диаметру d:
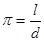
Это число известно с глубокой древности. Вавилонские, египетские, китайские и греческие математики нашли различные приближенные значения числа p:
3, 4 ,
,  ,
, 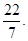 ,
,  ,
, 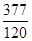
и другие. Рассматривая вписанные в окружность правильные 2n-угольники, Архимед умел вычислять p с большой точностью. В частности, он нашел, что
 < п <
< п < 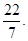
Лейбниц доказал, что число п можно представить в виде следующего ряда:
 (4)
(4)
(Заметьте, что дроби в правой части не являются десятичными.) Этот ряд позволяет находить приближенные значения числа п. Например, мы можем переписать равенство (4) так:
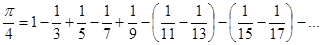
В скобках стоят положительные числа. Поэтому, «отбросив» их, мы увеличиваем правую часть:
 <
<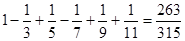
Умножив это равенство на 4, найдем оценку «сверху» для числа p: p<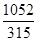
С другой стороны, из того же равенства (4) находим:
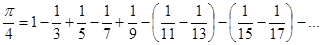
В скобках стоят положительные слагаемые. Поэтому, отбрасывая их, получаем:
 <
<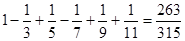 ,
,
что дает оценку «снизу» для числа p: p > . Итак, мы получили, что
. Итак, мы получили, что

 < p <
< p < 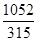
Это довольно грубая оценка истинного значения числа p. Ее можно улучшить, если взять для оценки не 5, а более слагаемых из ряда (4). Вот первые 15 точных знаков после запятой:
p= 3,141592653589793...
Другое очень известное в математике число — так называемое неперово4 число е — также может быть представлено в виде ряда:
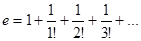
Здесь мы используем стандартное обозначение n! = 1 ´ 2 ´ 3 ... ´ n, которое читается «n факториал».
Чтобы найти приближенное значение числа е, нужно в сумме (5) оставить несколько слагаемых, а остальными пренебречь. Чем больше слагаемых мы оставим, тем точнее будет результат:
е = 2,718281828459045...
Используя ЭВМ, можно подсчитать числа е и n с любой точностью.
Числа n и е относятся к так называемым трансцендентным числам. Так называются числа, которые не могут быть корнями никакого уравнения вида (3) с целыми коэффициентами.
Подведем итоги. Назовем действительными или вещественными числами все бесконечные десятичные дроби. Обозначим множество всех таких чисел через R. Из предыдущих рассуждений вытекает, что множество R включает в себя множество Q всех рациональных чисел, поэтому можно записать
N Ì Z Ì Q Ì R.
Действительные числа, не являющиеся рациональными, называются иррациональными.
Весьма важный математический факт заключается в том, что множество действительных чисел является упорядоченным. Это означает, что любые два действительных числа можно сравнить между собой, т.е. указать, какое из них больше (или меньше). Процедура сравнения очень проста: нужно последовательно сравнивать цифры, стоящие на одинаковых позициях. Например, 2,381615... > 2,381529..., т.к. на первых четырех позициях соответствующие цифры одинаковы, а 6 > 5. Описанное правило сравнения работает при одном (и единственном) соглашении: не рассматривать периодические дроби с периодом 9. При этом множество действительных чисел, образно говоря, не сузится, т.к. всякую бесконечную периодическую дробь с периодом 9 можно заменить равной ей конечной десятичной дробью, например: 0,999... = 1, 0,42999... = 0,43, 2,65999... = 2,66 и т.п. (см. пример на с. 15).
Напомним свойства операций сложения и умножения действительных чисел:
переместительность или коммутативность:
а + b = b + а;
3.9. Буферные регистры АЛУ - лекция, которая пользуется популярностью у тех, кто читал эту лекцию.
сочетательность или ассоциативность (для сложения):
(а + b) + с = а + (b + с);
сочетательность или ассоциативность (для умножения):
(аb)с = а(bс);
распределительность или дистрибутивность: а(b + с) = ab + ас.
Числовые множества N, Z, Q, R являются примерами так называемых числовых систем, которые имеют специальные названия. Например, говорят кольцо целых чисел, поле рациональных чисел, поле действительных чисел.





















