Восстановление аналитической функции по ее действительной (мнимой) части
2020-06-032021-03-09zzyxelСтудИзба
Восстановление аналитической функции по ее действительной (мнимой) части.
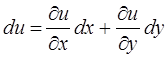


Опр. Функция  называется гармонической в области G, если в этой области выполняются условие:
называется гармонической в области G, если в этой области выполняются условие:

Утв. Если функция аналитическая, то ее действительная и мнимая части – гармонические функции.
Док-во:
 ;
;
Рекомендуемые материалы
[ПОЛНОСТЬЮ ВЕРНО by БЕЛОУСОВ] Д/З 9 ВАРИАНТ [ВСЯ КОМБИНАТОРИКА] [for IU7]
-62%
Теория поля
-62%
Теория поля
-62%
Теория поля
[Вариант 4] ДЗ по автоматам
-62%
Теория поля
 ;
;
т.к.  , складывая эти равенства, получаем
, складывая эти равенства, получаем  , т.е.
, т.е.
u – гармоническая функция. Аналогично v - гармоническая функция.
Доказано.
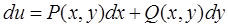


Пример.


"1 Определение определённого интеграла" - тут тоже много полезного для Вас.
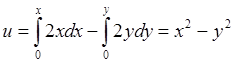
Опр. Функция f(z) называется однолистной в области G, если:

Пример. 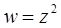
- не однолистная на всей плоскости
- однолистная в области 





















