Методы интегрирования и таблица интегралов

Лекция 2. Методы интегрирования и таблица интегралов.

Метод подведения под дифференциал.

Пусть известен интеграл (- первообразная для функции ). Тогда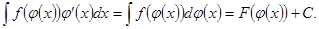

Главное здесь – «догадаться», как  представить в виде .

Доказательство.  по теореме о сложной функции. Следовательно, функция  и  являются первообразными для функции  и, по теоремам о первообразных, различаются на константу.

Этот метод применяется часто. Например, ,   .

Метод замены переменной.

Это – универсальный метод, метод подведения под дифференциал является частным случаем метода замены переменной.

Рекомендуемые материалы

Теорема. Пусть функция  непрерывно дифференцируема в некоторой области и имеет непрерывно дифференцируемую обратную функцию . Тогда  где .

Доказательство. Дифференцируя обе части, используя теоремы о производной сложной функции и инвариантность формы записи первого дифференциала, получим тождество дифференциалов.

, где . Из него следует равенство интегралов в левой и правой частях.

Заметим, что требования к обратной функции нужны, чтобы суметь возвратиться обратно, от переменной  к переменной .

Для вычисления интегралов вида , если вместо него удобно вычислять интеграл , пользуются методом интегрирования по частям.

  = - ,

 если интегралы в обеих частях соотношения существуют.

Докажем справедливость этой формулы. Дифференцируя произведение функций, получим  или

.

Интегралы левой и правой частей существуют().

Интегрируя, получим нужное соотношение.

Примеры.

.

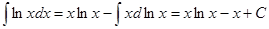
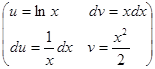
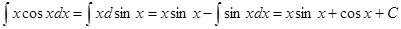
Вычислим интегралы , .

, 

                             .

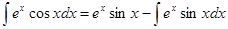
Теперь, подставляя второй интеграл в первый, получим

.

Аналогично, подставляя первый интеграл во второй, получим

.

Пополним таблицу интегралов, применяя методы интегрирования (в первой лекции получены четыре интеграла).

5.

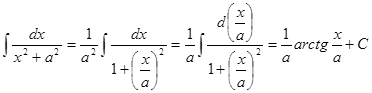
6.

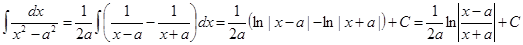
7.

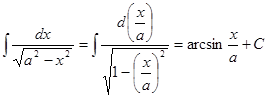
8.

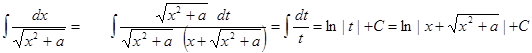
Здесь сделана замена переменной, подстановка - одна из подстановок Эйлера,

 ,,.

9.

                        ()

     .

            .

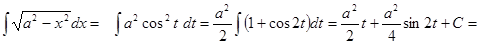
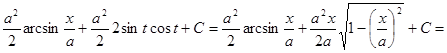
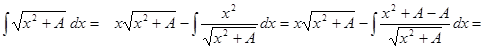
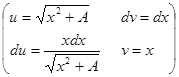
Перенося искомый интеграл из правой части в левую часть, получим

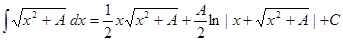
10.

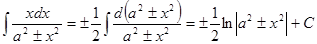
11.

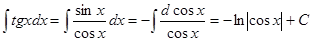
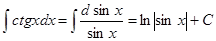
12.

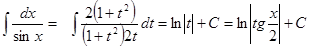
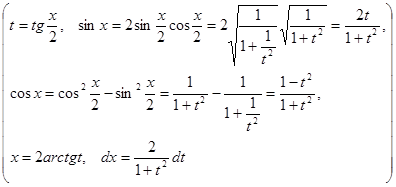
13.  - вывести самостоятельно.

Эти соотношения представляют собой таблицу основных интегралов.

Интегрирование выражений, содержащих квадратный трехчлен.

Квадратный трехчлен , выделяя полный квадрат, можно привести к виду

= ,

где ,                       .

Знак «+» выбирается, если , знак «-» выбирается, если . Если .

1. .

Если , то  .

Если , то .

Если , то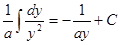

2. .

Если ,,  то под корнем стоит отрицательное число, интеграл в функциях действительной переменной вычислить не удастся.

Если , , то = .

Если , , то = .

Если , то .

Если , то =.

3. =

.

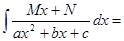
Интеграл  вычислен в п.1.

4. =

.

Интеграл  вычислен в п.2.

Заметим, что интегралы 5 –10 таблицы интегралов также содержат приведенный квадратный трехчлен.

Примеры.

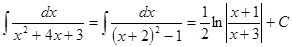
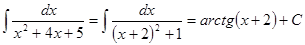
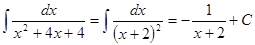
Бесплатная лекция: "5.3. Вопросы для самопроверки" также доступна.

.
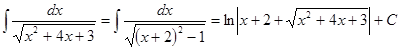
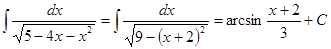
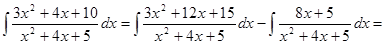
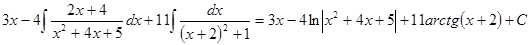
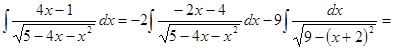