Достаточные условия дифференцируемости функции комплексного переменного (сформулировать и доказать)

Достаточные условия дифференцируемости функции комплексного переменного (сформулировать и доказать)

Производная функции комплексной переменной вводится так же, как и для функции действительной переменной

.

Функция  называется дифференцируемой в точке , если ее приращение в этой точке можно представить в виде

, то есть  - бесконечно малая при . Главная линейная относительно 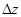 часть приращения функции в точке ,  называется дифференциалом функции в точке , ().

Замечание. Функция двух переменных  называется дифференцируемой в точке (), если ее приращение в этой точке можно представить в виде

++,

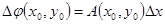
где ,  - бесконечно малые при ,

,  .

Рекомендуемые материалы

Теорема. Для того, чтобы функция  была дифференцируема в точке , необходимо и достаточно, чтобы существовала ее конечная производная в этой точке.

Доказательство. Проводится так же, как и для функции действительной переменной с использованием теоремы о связи функции, предела и бесконечно малой.

Необходимость. Пусть функция дифференцируема в точке , тогда

Ещё посмотрите лекцию "25. Орфей" по этой теме.

,

Делим обе части на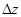

. Так как  - бесконечно малая при , то по теореме о связи функции, ее предела и бесконечно малой, .

Поэтому  - формула для вычисления дифференциала.

Достаточность. Пусть в точке  существует конечная производная функции . Тогда по теореме о связи функции, предела и бесконечно малой . Умножая на 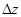, получим . Следовательно, функция дифференцируема в точке .

Функция называется дифференцируемой в области, если она дифференцируема в каждой точке этой области.