Вывести формулу для вычисления вычета в полюсе

Вывести формулу для вычисления вычета в полюсе

Если z₀ – правильная особая точка, то ряд Лорана превращается в ряд Тейлора, в котором нет отрицательных степеней , поэтому  =0.

Если z₀ – полюс первого порядка, то разложение в ряд Лорана в окрестности этой точки  не содержит степеней , ниже, чем –1 и содержит степень -1. Разложение выглядит так.

 . Умножим обе части на .

 Перейдем к пределу при , чтобы обратились в нуль все слагаемые в правой части, содержащие целые степени .

- формула для вычета функции в полюсе первого порядка.

В том случае, когда z₀ – полюс первого порядка функции вида

, можно получить удобную в вычислениях формулу для вычета.

= - формула для вычета функции в полюсе первого порядка. Здесь использованы условия      .

Рекомендуемые материалы

Пример. Найти вычеты функции  во всех особых точках конечной плоскости.

У функции два полюса первого порядка  .

По первой формуле

  .   

Применим вторую формулу

 . , .

В том случае, когда z₀ – полюс n-го порядка, то разложение в ряд Лорана в окрестности этой точки  не содержит степеней , ниже, чем –n и содержит степень –n . Разложение выглядит так.

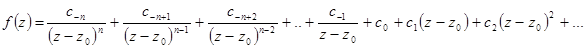
Умножим обе части на .

.

Рекомендуем посмотреть лекцию "Понятие религии и ее ранние формы".

Уничтожим степень при коэффициенте дифференцированием, его надо провести  раз. Получим

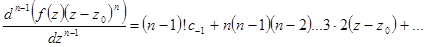
Перейдем к пределу при . Все слагаемые в правой части, содержащие целые степени  (второе, третье, четвертое и т.д.) обратятся в нуль. Отсюда имеем формулу для вычета функции в полюсе n – ого порядка:

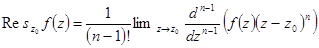
Пример. .  - полюс 1 порядка, z = 1 – полюс 2 порядка.

.